Частотные характеристики. 
Автоматика

Если на вход линейной непрерывной системы (или отдельного звена) подать синусоидальные (гармонические) колебания с постоянными амплитудой А_вх угловой частотой со и начальной фазой, равной нулю,.

то после затухания переходных процессов на выходе системы (или отдельного звена) также возникают синусоидальные колебания.

с той же угловой частотой со, но с другой амплитудой Л_вых и сдвинутые по фазе относительно входных колебаний на угол ср. Как известно из курса «Основы теории цепей» [2, ч. 1|, синусоидально изменяющиеся величины удобно изображать с помощью комплексных амплитуд. Комплексные амплитуды рассматриваемых здесь входных и выходных колебаний, описываемые уравнениями (2.25) и (2.26), можно записать как Х = А_пх и Y = A e^{J (p}.

— пых Подавая на вход системы гармонические колебания с постоянной амплитудой, но различными угловыми частотами со, на выходе системы тоже получаем гармонические колебания с теми же частотами, но различными для каждой угловой частоты амплитудами Д_шх(со) и фазами ср (со) относительно входных колебаний.

Введем в рассмотрение отношение комплексных амплитуд выходных и входных колебаний, называемое амплитудно-фазовой частотной характеристикой (АФЧХ) или комплексной частотной характеристикой (КЧХ):

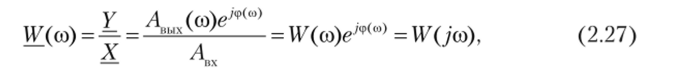
где U^(co) = W(у со) — АФЧХ, или комплексная частотная характеристика; j-yf-l — мнимая единица; W (со) — модуль АФЧХ, представляющий собой амплитудно-частотную характеристику (АЧХ), выражающую зависимость отношения амплитуд выходной и входной величин от частоты; ср (со) — аргумент АФЧХ, представляющий собой фазовую частотную характеристику (ФЧХ), выражающую зависимость разности фаз выходных и входных колебаний от частоты.

Амплитудно-фазовая частотная характеристика звена или системы не зависит от времени. Она отображает зависимость соотношения амплитуд и фаз выходной и входной величин от частоты. В отличие от временных характеристик (переходной и импульсной переходной) частотные характеристики выражают соотношения параметров установившихся выходных и входных колебаний при различных частотах. Однако они, как и временные характеристики, характеризуют динамические свойства звена или системы.

Комплексная функция W (co), или, как ее принято обозначать в теории автоматического регулирования, W (jco)_y может получиться чисто формально, без каких-либо вычислений, путем замены в выражении передаточной функции V (p) комплексной переменной р на чисто мнимую переменную усо. Например, для инерционного звена первого порядка в соответствии с формулой (2.11).

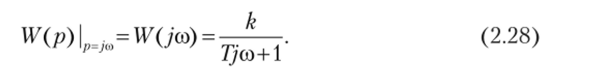
Чисто мнимую переменную усо можно представить как частный случай комплексной переменной, записываемой в общем виде как p = s+jco.

Итак, передаточная функция звена или системы при использовании частотного метода анализа является функцией комплексного переменного и сама является комплексной переменной. Известно, что любое комплексное число может быть изображено в виде вектора на комплексной плоскости, имеющей ось действительных и мнимых чисел.

Избавляясь от комплексной переменной в знаменателе умножением и делением выражения (2.28) на сопряженное знаменателю комплексное число (1-усоГ), получаем.

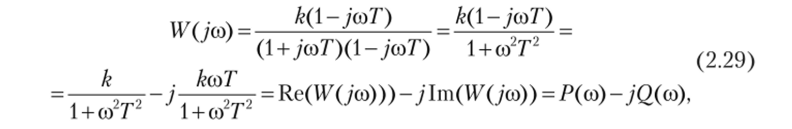
где Re (M^/(;co)) — проекция вектора W (j (o) па положительную действительную ось комплексной плоскости (вещественная составляющая),.

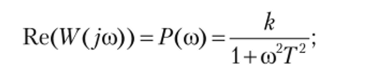
-lm (W (j (o) — проекция вектора W (ja> на мнимую отрицательную ось комплексной плоскости (мнимая составляющая),.

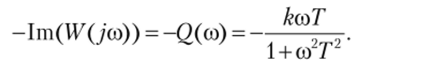
При изменении угловой частоты со от 0 до вектор У (/со), изображающий комплексную переменную, меняет свой модуль U^co) и фазу (угол сдвига) (р (со) в соответствии с выражениями:

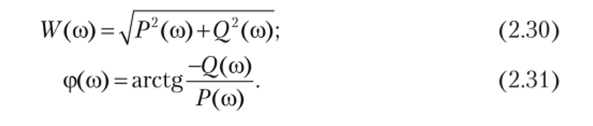
Итак, при изменении угловой частоты со от 0 до вектор W (j меняет свое положение на комплексной плоскости таким образом, что каждой угловой частоте со соответствует свой вектор. При этом конец вектора при его изменении опишет некоторую траекторию, называемую годографом. Следовательно, годограф вектора 1К (/со) и является амплитуднофазовой частотной характеристикой (АФЧХ) звена или системы.

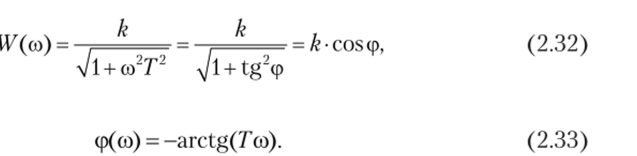
Годограф комплексной переменной НД/со), как функция угловой частоты со, согласно выражению (2.28), представляет собой АФЧХ, изображенную на комплексной плоскости (рис. 2.12, а). Для этого случая модуль вектора получен, но формуле, а угол его поворота Следовательно, при со = 0 модуль амплитудно-фазовой частотной характеристики W₀ =k, а при со = ос модуль АФЧХ W_y =0.

Поскольку угол ср при всех значениях со отрицательный, то годограф располагается в четвертом квадранте. При со = 0 угол ф₀ = 0°, а при со = оо угол ф_х = -90°.

Из выражения (2.32) следует, что модуль передаточной функции может быть представлен как проекция постоянной величины k на линию, проходящую иод углом ф к оси действительных чисел. Это означает, что при всех значениях угловой частоты со вектор, изображающий передаточную функцию инерционного звена перемещается по окружности, опирающейся на отрезок, лежащий между точками (k; j0) и (0; j0). Эта полуокружность и является годографом вектора передаточной функции инерционного звена.

На графике АФЧХ отмечают частоты, при которых построены векторы данной характеристики, и стрелкой указывают направление возрастания частоты. На рис. 2.12, б показаны зависимости вещественной и мнимой составляющих от угловой частоты со.

По выражениям (2.32) и (2.33) можно построить отдельно АЧХ и ФЧХ. Эти характеристики представлены на рис. 2.13.

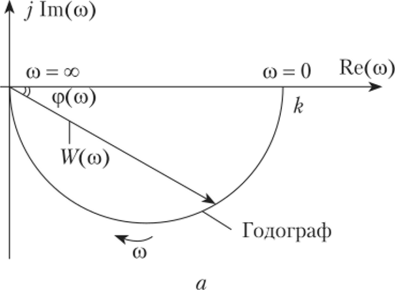
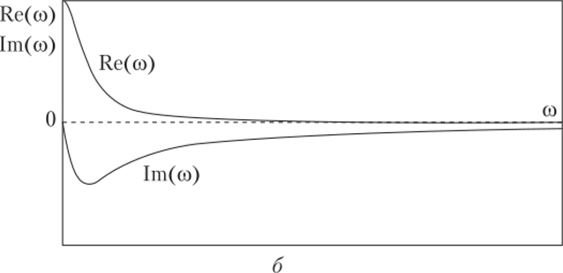
Рис. 2.12. Амплитудно-фазовая частотная характеристика апериодического звена первого порядка (а) и ее составляющие (б).

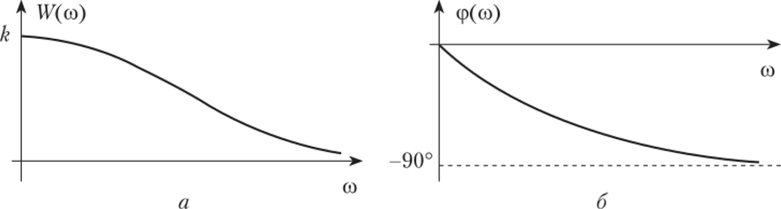
Рис. 2.13. Амплитудная и фазовая частотные характеристики апериодического звена первого порядка:

а — АЧХ; б — ФЧХ Амплитудно-частотная характеристика инерционного звена имеет почти горизонтальный участок при малых значениях частот и резко снижается при больших значениях частот. Отсюда можно заключить, что инерционное звено пропускает низкие частоты и «срезает» высокие. Это свойство инерционных звеньев используют при создании фильтров.

Постройте в интегрированном пакете MATLAB частотную характеристику линейного инерционного звена, используя его передаточную функцию.

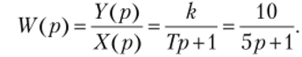
Решение.

Воспользуемся операционной средой библиотеки моделирования Simulink интегрированного пакета MATLAB. Для построения S-модели указанного звена используем, как и в примерах 2.1 и 2.2, блок Transfer Fen (блок передаточной функции), который представляет собой модель линейного звена с заданной передаточной функцией в виде отношения полиномов заданной степени (рис. 2.14). S-модель и частотная характеристика линейного инерционного звена приведены на рис. 2.14.

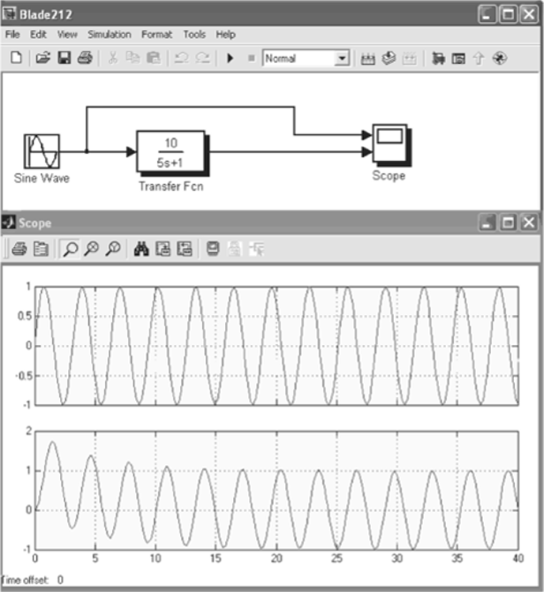
Рис. 2.14. S-модель и частотная характеристика линейного инерционного звена.

Синусоидальный сигнал на вход инерционного звена подается от источника синусоидального воздействия (Sine Wave). Этот источник берется из раздела Sources (блоки источников питания) библиотеки Simulink. Амплитуда сигнала задана равной 1 В, а угловая частота колебаний со = 2 рад/с. Амплитуда выходного сигнала и угол сдвига, определяемые с использованием формул (2.32) и (2.33), составляют соответственно 0,995 В и -84,3°, что хорошо совпадает с данными, полученными на рис. 2.14.

Как будет показано ниже, при последовательном соединении звеньев в сложных системах их передаточные функции перемножаются. Поэтому эквивалентная частотная характеристика W^jco) получается перемножением амплитуд и сложением фазовых углов последовательно включенных элементов. Для решения практических задач удобнее операцию перемножения амплитуд заменить операцией сложения их логарифмов. Поэтому в инженерных расчетах чаще всего амплитудную и фазовую частотные характеристики изображают в логарифмическом масштабе, что позволяет в значительной степени сократить объем вычислительных работ. При переходе к логарифмам операции умножения передаточных характеристик звеньев заменяют на более простые операции сложения их показателей степени или логарифмов. При этом для нахождения результирующей переходной характеристики системы характеристики отдельных звеньев можно складывать графически.

Логарифм АЧХ характеризует степень усиления сигнала. Логарифмической единицей усиления или ослабления мощности сигнала при прохождении его через какое-либо устройство при выражении десятичным логарифмом величины отношения мощности сигнала на выходе Р_вых к мощности сигнала на входе Р_ах в технике принят бел (Б). В соответствии с этим определением усиление мощности сигнала в 10 раз равно 1 Б:

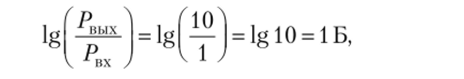
а усиление мощности сигнала в 100 раз равно 2 Б:

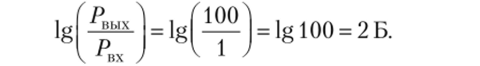
В автоматике чаще пользуются не мощностями сигналов, а их амплитудами. Так как мощность сигнала пропорциональна его амплитуде в квадрате, то можно записать.

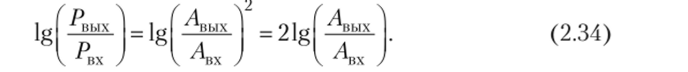
Поскольку бел является достаточно крупной единицей усиления (ослабления) мощности (увеличению мощности в 10 раз соответствует 1 Б), то за единицу измерения ее на практике принята в 10 раз меньшая единица — децибел (дБ): 1 дБ = 0,1 Б или 1 Б = 10 дБ. С учетом этого можно записать.

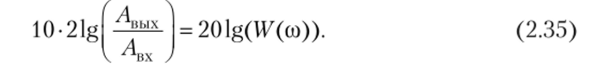
Зависимость (2.35) называют логарифмической амплитудно-частотной характеристикой (ЛАЧХ). Таким образом, изменению отношения двух амплитуд в 10 раз соответствует изменение усиления на 20 дБ, в 100 раз — на 40 дБ, в 1000 раз — на 60 дБ и г. д.

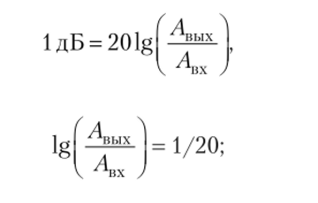
Вычислим, какому отношению амплитуд соответствует 1 дБ, 2 дБ и т. д. (табл. 2.2):

следовательно, отсюда.

Таблица 2.2

Соотношение величины децибела с отношением амплитуд.

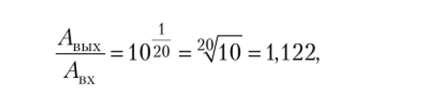
т.е. 1 дБ соответствует усилению или ослаблению в 1,122 раза.

Фазовая частотная характеристика ср (со), построенная в полулогарифмическом масштабе в виде зависимости угла (р в градусах или радианах от логарифма угловой частоты (lg со), называется логарифмической фазовой частотной характеристикой (ЛФЧХ). За единицу измерения частоты сигнала принимают логарифмическую единицу — декаду (дек). Декадой называется интервал частот между какой-либо величиной частоты и ее десятикратным значением. В логарифмическом масштабе частот отрезок в 1 дек не зависит от частоты и имеет длину, равную lgf ——) = lg 10 = 1.

V со У Обычно ЛАЧХ и ЛФЧХ строят совместно, используя общую ось абсцисс (ось частот). При использовании логарифмического масштаба начало координат невозможно взять в точке со = 0, так как lg 0 = -оо и нулевая точка должна находиться слева, в минус бесконечности. Поэтому начало координат берут в любой удобной точке со > 0 в зависимости от интересующего диапазона частот. При построении ЛАЧХ по оси ординат откладывают логарифмическую амплитуду в децибелах L (co) = 201g (lT (со)), а по оси абсцисс — угловую частоту со в радианах в секунду (рад/с = с^-1) или в lg со (дек). На рис. 2.15 показан пример ЛАЧХ, построенной с использованием формулы (2.32) при k = 6 и Т= 0,03 с.

Нуль логарифмической амплитуды соответствует значению W (co) = 1, т. е. когда усиление сигнала равно единице, поскольку lgl = 0. Если W (со) < 1, т. е. выходная амплитуда меньше входной, что соответствует ослаблению сигнала, то значения ЛАЧХ отрицательные и на графике они находятся ниже оси абсцисс.

Логарифмическую ФЧХ строят в системе координат с такой же осью абсцисс, что и у ЛАЧХ, но по оси ординат в линейном масштабе откладывают угол ср (со), в градусах или радианах. Обычно ЛФЧХ строят под ЛАЧХ для того, чтобы можно было сопоставить изменение фазы с изменением амплитуды при одинаковых частотах.

Точку пересечения ЛАЧХ с осью абсцисс называют частотой среза и обозначают со_ср. Эта точка соответствует значению.

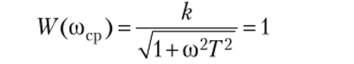
(усиление равно единице) и соответственно lg (W (co_cp)) = lg 1 = 0, т. е. прохождению амплитуды сигнала через звено в натуральную величину. Поэтому говорят, что на частоте среза звено или система теряет усилительные свойства. При частоте большей, чем частота среза, сигнал на выходе становится меньше, чем сигнал на входе, т. е. звено не усиливает, а ослабляет входной сигнал. При заданных параметрах частота среза.

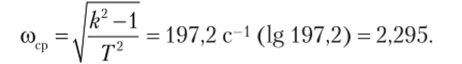
1(со) = 201g (W (oo)), дБ.

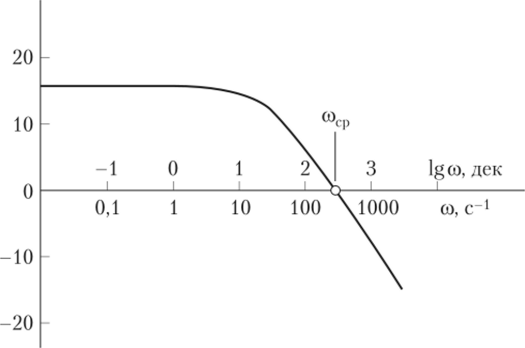
Рис. 2.15. Пример построения логарифмической амплитудно-частотной характеристики.

Рассмотренные здесь частотные характеристики можно получить экспериментально и, но ним определить параметры исследуемого звена и его передаточную функцию. Частотные характеристики используют при расчете переходных процессов графоаналитическим методом, который называют частотным методом. Частотный метод, разработанный В. В. Солодовниковым, позволяет с достаточной степенью точности рассчитать переходные процессы в замкнутой системе по ее вещественной частотной характеристике Re (co). Для этого вещественную частотную характеристику представляют в виде суммы трапецеидальных или треугольных составляющих. Для каждой составляющей с помощью приводимых в справочниках по САР таблиц и номограмм определяют переходную функцию. Далее все переходные функции суммируют и получают график переходного процесса.

Заметим, что часто вместо вещественной частотной характеристики пользуются логарифмической амплитудной характеристикой.