Средние величины и показатели вариации

Построение средних величин

Понятие средней величины большинству людей хорошо известно. Обычно среднюю величину воспринимают как отражение общего в значениях признака у множества единиц. Таковы, например, средний возраст жителя страны, средний размер семьи в районе, средний размер прибыли предприятия.

Действительно, средняя величина — это обобщающая оценка признака у множества объектов, которая отражает его характерное значение. Характерное значение фиксирует типическую величину признака, в котором находит выражение своеобразие данной группы объектов и ее отличие от значений признака у других групп.

Например, средняя заработная плата работников в разных видах деятельности в 2015 г. в России составила, тыс. руб.^[1]:

• • сельское хозяйство — 19,5;
• • добыча полезных ископаемых — 63,7;
• • обрабатывающие производства — 31,8;
• • строительство — 29,9.

В разном уровне оплаты, т. е. в разной средней заработной плате работника, проявляются особенности организации труда в разных видах деятельности и в конечном счете — общественное признание того или иного труда.

В приведенном примере даны средние, которые рассчитаны по группам, состоящим из объектов одного вида деятельности и которые в этом смысле могут быть названы однородными. Подобные средние называются групповыми. Они интересны тем, что связаны с конкретными объектами и условиями их существования. Когда производится расчет групповых средних, то при одинаковых, например, условиях труда происходит взаимное погашение влияния случайных причин на заработную плату. В то же время при расчете групповой средней усиливается влияние особых, специфических условий, поскольку они действуют постоянно и в одном направлении. В групповой средней отражаются особенности однородных объектов и погашается случайность. Именно, но этим причинам групповые средние находят широкое практическое применение.

Когда речь заходит об общей средней, но множеству, включающему несколько однородных групп, то при ее расчете погашается действие не только случайных, но и групповых особенностей. Так, общая средняя заработная плата занятого в экономике страны в 2015 г. составила 34 тыс. руб. В ней не отражаются особенности оплаты труда в разных видах деятельности, а показывается лишь общий уровень оплаты труда занятых в ЭКОНОМИКС.

Сравним среднюю заработную плату работников разных видов деятельности в 2010 и 2015 гг. в экономике РФ (табл. 6.1).

Таблица 6.1

Средняя заработная плата в разных видах деятельности и ее изменения, тыс. руб.

Источник: Россия в цифрах. 2016. Табл. 7.7.

В темпах изменения средних по видам деятельности, т. е. в групповых средних, проявляются частные закономерности изменения заработной платы: в интервале от 1,41 до 1,82 раза. Сравнивая изменение общей средней, устанавливаем общую закономерность изменения уровня заработной платы в экономике страны: увеличение в 1,62 раза.

Всесторонний анализ предполагает совместное использование общих и групповых средних: это позволяет характеризовать общие закономерности развития и особенности их проявления в конкретных условиях.

Расчет средней выполняется в два этапа. На первом этапе производится обобщение индивидуальных значений изучаемого признаках, у множества, состоящего из п единиц: {х-}. На втором этапе полученный результат распределяется между множеством этих п единиц: {х,} + п — х.

При обобщении значений признака у п объектов множества {х,} происходит взаимное погашение влияния случайных причин и усиливается действия неслучайных систематических факторов. При распределении обобщенного значения признака между п единицами множества {х_;-} п определяется средняя типическая его величина х у одной абстрактной единицы. В результате имеем либо групповую среднюю по группе однородных объектов: {х_;}-н п = х, либо общую среднюю для всего изучаемого множества {х,} -г- п = х.

Для расчета средних существуют несколько способов, которые отличаются порядком обобщения и распределения.

Средняя арифметическая обобщает индивидуальные значения x_f суммированием, а равномерное распределение — делением суммы дг, на число единиц, участвующих в расчете: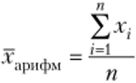

Частое использование арифметической средней объясняется ее особыми свойствами, которые делают ее расчет более простым, а результат — легко проверяемым.

Сумма отклонений значений признака от арифметической средней равна нулю:

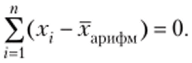
Если значения признака х, изменить на число Л, то арифметическая средняя изменится на это же число: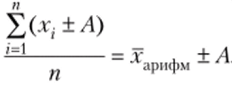

Если значения признака х, увеличить в А раз, то арифметическая средняя увеличится в А раз: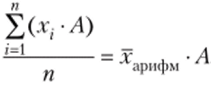

Если значения признака Xj уменьшить в А раз, то арифметическая средняя также уменьшится в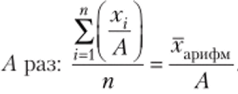

Средняя гармоническая используется в тех случаях, когда расчет выполняется по значениям признака, который связан с изучаемым признаком обратной зависимостью, т. е. при условии, что V определяется по значениям признака

Например, показатель выработки продукции на работника: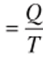

•Показатель трудоемкости единицы продукции: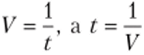

Показатели выработки и трудоемкости находятся в обратной зависимости: 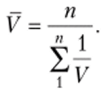. Поэтому при расчете средней выработки по значениям трудоемкости следует применять гармоническую среднюю.

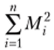
Средняя квадратическая применяется в случаях, когда при обобщении значений признака А/, необходимо избежать нулевого результата, так как квадратов 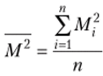рассчитывают среднюю: 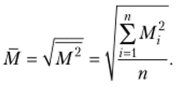, а из полученной средней извлекают квадратный корень:

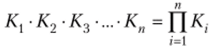
Наиболее часто квадратическая средняя применяется при расчете показателей вариации и оценок различий структур множества.

Средняя геометрическая обобщает значения признака путем расчета их произведения: 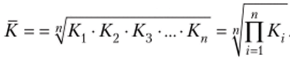, а из результата извлекается корень п-й степени:

Наиболее логически оправдано применение геометрической средней при расчете из цепных темпов роста среднего темпа роста:

Разный порядок расчета средних объясняет разные значения результата. Свойство мажорантности средних величин устанавливает зависимость величины средней от показателя ее степени: чем выше показатель степени средней, тем больше ее значение. Каждая из рассмотренных средних представляет собой разновидность степенной средней (табл. 6.2).

Таблица 6.2

Формы средних величин.

Форма средней.	Расчетная формула.	Показатель степени средней ©.
Квадратическая.		с = 2.
Арифметическая.		с — 1.
Геометрическая.		с = 0.
Гармоническая.		с = -1.

В качестве иллюстрации свойства мажорантности выполним по данным о численности населения федеральных округов РФ расчет разных средних (табл. 6.3).

Приведенный пример подтверждает, что с увеличением степени средней: от наименьшей — для гармонической, до наибольшей — для квадратической, величина средней увеличивается. Свойство мажорантности средних можно представить в виде неравенств: V < К <�х < М.

Из свойства мажорантности следует вывод о том, что выбор способа расчета средней не может быть произвольным. Он должен основываться на смысловом содержании исходных данных и на условиях применения конкретной формы средней.

Известно, что геометрическая средняя используется для обобщения темпов роста, а квадратическая — в тех случаях, когда сумма значений признака равна нулю. Поэтому наиболее востребованными практикой являются арифметическая и гармоническая формы средних.

По особым правилам проводится расчет средних из абсолютных и относительных значений изучаемых характеристик. Рассмотрим особенности расчета средних на примере данных, но федеральным округам РФ за 2014 г. (табл. 6.4).

В табл. 6.4 использованы следующие признаки и их обозначения.

Численность занятых в экономике федерального округа, млн человек Р,.

Численность занятых в процентах от численности всего населения федерального округа, % — С,.

Приходится оборота розничной торговли за год в среднем на одного жителя федерального округа, тыс. руб. — Т_г

Приходится инвестиций в среднем на одного занятого в экономике федерального округа, тыс. руб. — R_r

Таблица 63

Расчет средней численности населения федеральных округов РФ с применением различных средних.

Федеральный округ.	Численность населения. iia01.0i.201G. (Н,),. млн чел.
Центральный.	39,1.	1528,8.	39,1.	39,1.	0,0256.
Северо-Западный.	13,9.	193,2.	13,9.	543,5.	0,0719.
Южный.	14,0.	196,0.	14,0.	7609,0.	0,0714.
Северо-Кавказский.	9,7.	94,1.	9,7.	73 807,3.	0,1031.
Приволжский.	29,7.	882,1.	29,7.	2 192 076,8.	0,0337.
Уральский.	12,3.	151,3.	12,3.	26 962 544,6.	0,0813.

Федеральный округ.	Численность населения на 01.01.2016. <�н,),. млн чел.
Сибирский.	19,3.	372,5.	19,3.	520 377 110,8.	0,0518.
Дальневосточный.	6,2.	38,4.	6,2.	3 226 338 087.0.	0,1613.
Крымский.	2,3.	5,3.	2,3.	7 420 577 600,0.	0,4348.
Итого.	146,5.	3461,7.	146,5.	И 196 529 418,1.	1,0349.
Квадратическая средняя (см. формулу (6.1)).		19,6.
Арифметическая средняя (см. формулу (6.2)).			16,3.
Геометрическая средняя (см. формулу (6.3)).				13,1.
Гармоническая средняя (см. формулу (6.4)).					8,7.

Источник: Россия в цифрах. 2016. Табл. 1.3.

Особенность абсолютных значений признака в том, что они непосредственно относятся к единице совокупности и определяют ее абсолютные размеры. Например, для федерального округа как единицы множества абсолютными значениями будут численность населения, численность занятых, стоимость произведенной продукции, стоимость основного капитала, прибыль от реализации продукции и т. п. Приведенные признаки относятся непосредственно к федеральному округу, называются первичными и по их значениям можно определить размеры каждого изучаемого объекта. При обработке абсолютных значений этих признаков точно учитывается размер каждой единицы и поэтому нет никаких ограничений для обобщения их значений путем непосредственного суммирования. Средняя, при расчете которой обрабатываются значения единственного признака, называется простой. Например, простая средняя применяется для расчета средней численности занятых в экономике одного федерального округа (табл. 6.4).

Таблица 6.4

Расчет средних значений экономических показателей по федеральным округам РФ, 2014 г.

Источник: Россия в цифрах. 2016. Табл. 1.3.

Примечание: знак «х» означает, что данная ячейка не подлежит заполнению.

Расчет выполняется по следующей формуле:

В экономике федерального округа в среднем за 2014 г. было занято 8,5 млн человек.

Средние из относительных значений определяются, но более сложной схеме. Особенность относительных значений в том, что они не связаны непосредственно с размерами изучаемых единиц, а без этого учета подсчет точной средней обычно невозможен. В подобных случаях в расчет должны включаться дополнительные значения характеристик, которые отражают абсолютные размеры каждой из изучаемых единиц. В расчете средней помимо изучаемой участвует дополнительная характеристика или вес, поэтому средняя называется взвешенной. При расчете взвешенной средней в качестве веса всегда выступает абсолютная характеристика или первичный признак. Вес позволяет учесть абсолютные размеры каждой единицы и обеспечивает расчет точного значения средней.

В приведенном примере характеристики С, Г, и являются относительными, поэтому прямое суммирование их значений недопустимо. Для определения схемы расчета их средних значений установим порядок расчета их индивидуальных значений.

Расчет процента занятых от численности всего населения выполняется, но следующей формуле: В расчетной формуле неизвестна по условию задачи численность населения. Для определения ее значения выразим численность населения через численность занятых Р, и известные значения процента занятых от численности всего населения С:

или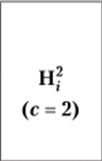

Чтобы определить численность населения в млн человек, необходимо разделить численность занятых в экономике Р, на их долю в численности всего населения С,. Поэтому необходимо значения С, перевести из процентов в доли единицы: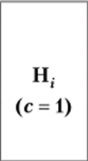

Рассчитаем неизвестное значение численности населения в дополнительной расчетной графе (табл. 6.5, гр. 2).

При известных значениях численности занятых Р, и численности всего населения 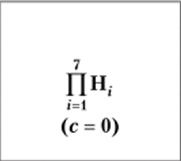расчет процента занятых в буквенной форме имеет вид.

Общая средняя С рассчитывается по той же схеме, что и индивидуальные значения характеристики С,-. Разница лишь в том, что при расчете общей средней С используются итоговые значения сравниваемых признаков: численности занятых, млн человек ^и численности всего населения, млн человек 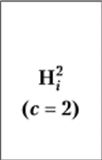То есть расчет общей средней С но восьми федеральным округам выполняется по формуле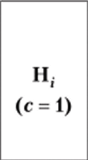

Расчет средних значений относительных характеристик по экономике РФ в 2014 г.

Таблица 6.5

Составлено и рассчитано по: Россия в цифрах. 2016. Табл. 1.3.

В Экономикс России в 2014 г. доля занятого населения составляла в среднем 47,2% численности всего населения. Расчет выполнен по гармонической средней взвешенной, в которой весом выступил первичный признак P_t — численность занятых в экономике.

Аналогичные рассуждения лежат в основе расчета средних значений двух других относительных характеристик: средней стоимости оборота розничной торговли на одного жителя, Т тыс. руб., и средней стоимости инвестиций на одного занятого, R тыс. руб.

Индивидуальные значения стоимости оборота розничной торговли на одного жителя, тыс. руб., рассчитываются как результат сравнения оборота розничной торговли за год, млрд руб., с численностью всего населения, млн человек:

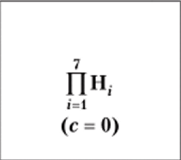
По условию задачи неизвестна стоимость оборота розничной торговли. Поэтому выразим неизвестные значения оборота розничной торговли через известные значения численности всего населения и заданные в условии задачи значения Т_г Искомый оборот розничной торговли (товарооборот) есть произведение численности всего населения и величины товарооборота на одного жителя:

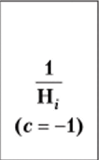
Величина оборота розничной торговли измеряется в млрд руб., так как при его расчете численность жителей в млн человек умножаем на товарооборот на одного жителя в тыс. руб.

Определим неизвестные значения оборота розничной торговли за год в гр. 5 табл. 6.5.

Расчет общего среднего значения оборота розничной торговли на одного жителя, тыс. руб., Т, выполним по итоговым значениям суммы оборота розничной торговли, млрд руб., 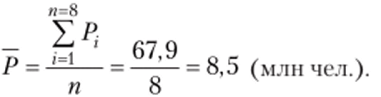, и суммарной численности всего населения, млн чел., . Расчетная формула имеет вид

В 2014 г. на одного жителя в Российской Федерации приходилось в среднем 181,5 тыс. руб. оборота розничной торговли. При расчете использована арифметическая взвешенная средняя, а весом выступают абсолютные значения общей численности населения:

Для расчета стоимости инвестиций на одного занятого необходимо стоимость инвестиций, млрд руб., сравнить с численностью занятых в экономике, млн человек:

По условию неизвестна стоимость инвестиций, поэтому для расчета ее значений следует выразить инвестиции через известные значения численности занятых Pj и через заданные в условии задачи величины инвестиций на одного занятого /?:

или.

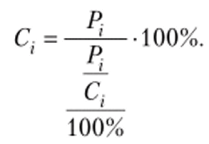
Подсчет неизвестного значения общей суммы инвестиций выполним в гр. 7 табл. 6.5.

Рассчитанные значения общей суммы инвестиций позволяют определять индивидуальные значения инвестиций на одного занятого по формуле.

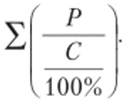
Для РФ в целом среднее значение инвестиций в расчете на одного занятого К рассчитаем как отношение суммы инвестиций за год ?/? Р к сумме численности занятых.

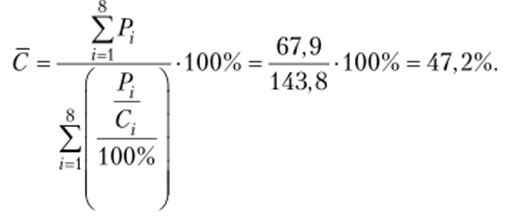
В 2014 г. инвестиции в расчете на одного занятого составили в среднем 198,8 тыс. руб. При расчете использована средняя арифметическая взвешенная, весом являются абсолютные значения численности занятых.

Завершающим этапом расчета средних является проверка правильности результата. Логическая проверка основана на анализе схемы расчета индивидуальных значений характеристики и на определении смысла признакавеса. Счетный контроль устанавливает, находится ли средняя в интервале от минимального до максимального значения изучаемого признака. Если выполняется условие X_mjn <�Х <�Х_тах, то расчет средней выполнен верно. Если данное условие не выполняется, то в расчете допущены ошибки, которые необходимо выявить и исправить.

В нашем примере (см. табл. 6.5) для всех значений рассчитанных средних данное условие выполняется:

простая арифметическая Р = 8,5, 3,3 < Р < 19,0;

взвешенная гармоническая С = 47,2, 36,3 < С < 53,2;

взвешенная арифметическая Т = 181,5, 134,7 < Т < 231,4 ;

взвешенная арифметическая R = 198,8, 142,9 < R < 383,3 .

Это означает, что в определении средних значений не допущено расчетных ошибок, а использование взвешенных средних для расчета средних из относительных величин позволило учесть размеры изучаемых единиц — федеральных округов РФ.

Подводя итог, напомним основные правила построения средних величин.

По абсолютным значениям признака допустим расчет простой средней. Как правило, в большинстве случаев применяется арифметическая средняя. Например, расчет Р.

По относительным значениям расчет выполняется, но взвешенной средней, в которой весом являются абсолютные значения первичного признака, связанного по смыслу с изучаемым признаком. Например, расчет С, Т и R.

В качестве веса используются значения признака, по отношению к которому рассчитаны относительные значения вторичного признака. Вес может отображаться весьма просто, как, например, при расчете С и R, где в качестве веса использована численность занятых Р_г Но он может иметь и сложное отображение, как, например, при расчете Г, у которого весом.

Р

была численность всего населения. Каким бы образом ни отображался признак-вес, он всегда должен представлять собой абсолютную оценку изучаемого объекта.

Выбор формы средней в большинстве случаев ограничен арифметической или гармонической, так как квадратическая и геометрическая применяются лишь в строго определенных случаях.

Арифметическая форма средней применяется в тех случаях, когда в условии поставленной задачи отсутствуют значения признака, который связан с изучаемым признаком прямой зависимостью, т. е. когда в расчетной формуле индивидуальных значений отсутствуют сведения о ее числителе. Примером могут быть расчеты Р, Т и R.

Если в расчетной формуле отсутствуют данные о знаменателе отношения, то используется гармоническая средняя. В этом случае изучаемый признак связан с неизвестным признаком обратной зависимостью, как, например, при расчете С.

Правильно выполненные расчеты позволяют получить точные средние значения, которые отражают характерную величину признака и представляют интерес при решении аналитических и прогнозных задач.

• [1] См.: Россия в цифрах. 2016. Табл. 7.7.