Расчеты на прочность и жесткость

Нагрузки на валы и оси передаются от насажденных деталей, соединительных муфт и в виде реакций связей. Эти нагрузки являются распределенными и для расчета заменяются сосредоточенными силами. Окружные и радиальные силы, действующие в зацеплении зубчатых колес, прикладываются в середине зубчатого венца, проектируются на взаимно перпендикулярные оси (у и г) и переносятся на ось вала. При переносе… Читать ещё >
Расчеты на прочность и жесткость (реферат, курсовая, диплом, контрольная)
На валы и оси передаточных механизмов действуют поперечные силы, например от зацепления зубчатых колес, натяжения ремней и цепей. В конических, косозубых цилиндрических и червячных передачах возникают продольные силы. Изгибающий момент в поперечном сечении вала зависит как от нагрузок, действующих на вал, так и от его линейных размеров. На стадии проектирования длина вала не известна. Поэтому конструирование и расчет вала проводится в три этапа: проектировочный расчет, конструирование вала и проверочный расчет на прочность.
Проектировочный расчет. Исходным размером для конструирования вала является диаметр наиболее нагруженного участка, положение которого можно определить по кинематической схеме механизма. При отсутствии данных об изгибающих моментах диаметр вала приближенно может быть найден по известной величине вращающего момента. Из условия прочности по кручению 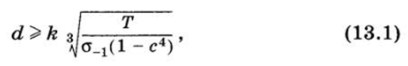
где d — диаметр вала (мм); Т — расчетная величина вращающего момента (Н • мм); — предел выносливости материала (МПа); с = d0/d; d0, d — диаметр отверстия и наружный диаметр вала; k — коэффициент, учитывающий влияние изгибающего момента. Для сплошного вала с = 0, для полого с = = 0,7…0,85, нижнее значение принимается при ограниченной жесткости вала. Значения коэффициента k задаются в зависимости от расположения зубчатых колес относительно опор и типа вала (табл. 13.3).
Конструирование вала. Полученное значение диаметра вала служит основанием для разработки его конструктивной формы. В соответствии с кинематической схемой и геометрическими размерами зубчатых колес, подшипников и других сопрягаемых деталей разрабатывается конструкция вала, обеспечивающая условия эксплуатации, технологичности изготовления и сборки. Номинальные диаметры вала согласуются со стандартным рядом нормальных линейных размеров. После конструктивной проработки выполняется проверочный расчет на прочность (см. пример на с. 240).
Таблица 13.3.
Вал. | Положение зубчатых колес. | ||
Симметричное. | Несимметричное. | Консольное. | |
Быстроходный. | 3,8. | 4,0. | 4,4. |
Тихоходный или промежуточный. | 3,0. | 3,1. | 3,2. |
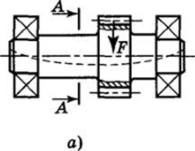
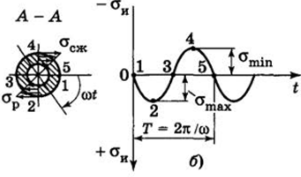
Проверочный расчет вала на усталостную прочность. Основными требованиями работоспособности валов и осей являются прочность и жесткость. Вращающиеся валы и оси рассчитываются на усталостную прочность, так как постоянные по значению и направлению поперечные силы вызывают в них переменные напряжения. Под действием поперечных сил (рис. 13.9, а) вал изгибается. При вращении вала его поперечное сечение меняет свою ориентацию относительно плоскости действия изгибающего момента Ми и напряжения изгиба изменяются по знакопеременному симметричному циклу.
М
(рис. 13.9, б) с амплитудой оа = ои = атах = «г и средним на;
" и пряжением ат = 0. Коэффициент асимметрии цикла Ra = = —— = -1. Если в сечении вала действует продольная сила,.
ашах вызывающая напряжения сжатия осж или растяжения ар, то цикл изменения напряжений — несимметричный. В этом случае параметры цикла напряжений определяются по формулам:
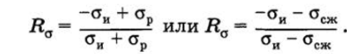
Величины амплитудных са и средних ст напряжений цикла определяются следующими зависимостями:

Цикл изменения касательных напряжений зависит от величины и направления крутящего момента. Для реверсивных механизмов при Tmax = IT^J цикл знакопеременный, симметричный (рис 13.10, а); в нереверсивных механизмах прерывистого действия — цикл отнулевой (рис. 13.10, б).
а) б).
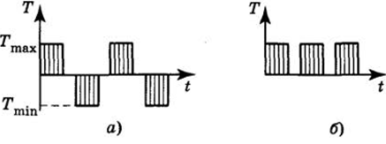
Рис. 13.10.
В проверочном расчете вала можно выделить следующие этапы:
- ? составление расчетной схемы;
- ? определение расчетных нагрузок и перенос их на ось вала;
- ? определение опорных реакций и построение эпюр изгибающих, крутящих моментов и нормальных (осевых) сил;
- ? выбор опасных сечений;
- ? определение расчетных напряжений и запасов прочности в опасных сечениях.
Для расчета вал часто представляется как статически определимая балка, для этого одна из опор (незафиксированная в осевом направлении) считается шарнирно-подвижной. Подшипники, одновременно воспринимающие радиальные и осевые нагрузки, схематизируются как шарнирно-неподвижные. При установке вала в радиальных подшипниках точками опор считается середина ширины каждого подшипника (рис. 13.11, а, б). Для двух подшипников в одной опоре вала условная опора располагается так, как показано на рис. 13.11, в. При установке радиально-упорных подшипников опора вала находится на пересечении линии, проходящей через точку контакта, с осью вала (рис. 13.11, г, д). Расстояние а между точкой пересечения и опорным торцом наружного кольца подшипника определяется по формулам: для радиально-упорных шарикоподшипников (рис. 13.11, г) 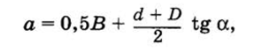
где В, d, D — ширина, внутренний и наружный диаметры; а — угол контакта;
для конических роликоподшипников (рис. 13.11, д).

где Т — ширина подшипника; е — коэффициент осевого на гружения, зависящий от угла контакта (см. табл. 14.2).
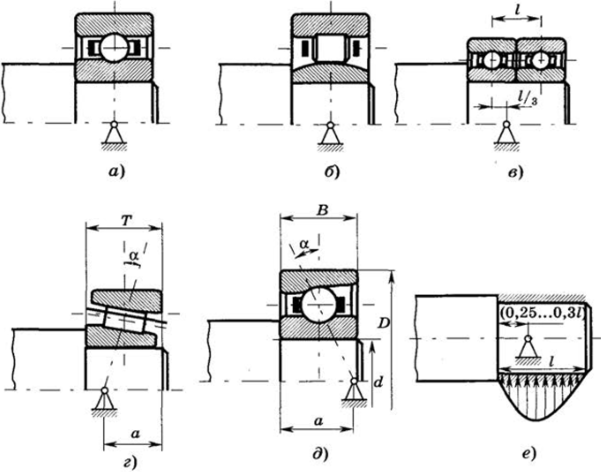
Рис. 13.11.
В валах, опирающихся на подшипники скольжения, опора располагается на расстоянии (0,25…0,3)/ от внутреннего торца подшипника (рис. 13.11, е).
Нагрузки на валы и оси передаются от насажденных деталей, соединительных муфт и в виде реакций связей. Эти нагрузки являются распределенными и для расчета заменяются сосредоточенными силами. Окружные и радиальные силы, действующие в зацеплении зубчатых колес, прикладываются в середине зубчатого венца, проектируются на взаимно перпендикулярные оси (у и г) и переносятся на ось вала. При переносе осевых сил к оси вала добавляется действие изгибающего момента. Далее определяются реакции опор в двух плоскостях (вертикальной и горизонтальной) и строятся эпюры изгибающих (М2 и Му) и крутящего (Мк) моментов. Если присутствует осевая нагрузка, строится эпюра нормальных сил N. Для наглядности полезно построить эпюру суммарного изгибающего момента Ми — JM| + М*.
Ответственным моментом является выбор расчетного сечения. Большое влияние на сопротивление усталости оказывает концентрация напряжений. Поэтому при расчете на устал ость опасное сечение может не совпадать с сечением, в котором действуют максимальные моменты, и в качестве опасного выбирается сечение, близкое к месту концентрации напряжений, так называемому концентратору. Иногда не удается сразу выделить одно опасное сечение, тогда расчет ведется по нескольким сечеРис. 13.12.
ниям. Для валов концентраторами напряжений являются шпоночные пазы, шлицы, резьба, ступенчатые переходы с галтелью, поперечные отверстия.
Для каждого из выбранных сечений определяются расчетные коэффициенты запаса прочности п и сравниваются с допускаемым значением [п]. Обычно [п] = 1,5.Л, 7. Проверку прочности ведут по формуле 
где па и пх — запасы прочности по нормальным и касательным напряжениям:
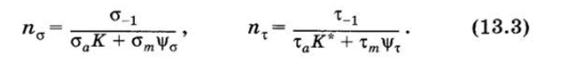
Здесь a_lf t_j — пределы выносливости материала вала по нормальным и касательным напряжениям; К и К* — коэффициенты снижения пределов выносливости детали для нормальных и касательных напряжений; оа и та — амплитуды напряжений цикла; от ихт — средние напряжения цикла; |/0 и |/т — коэффициенты чувствительности материала к асимметрии цикла напряжений (табл. 13.4).
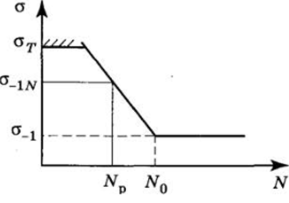
В механизмах с относительно малым ресурсом, например в авиационной и космической технике, детали не вырабатывают базовое число циклов N0 и расчет ведется по пределу ограниченной выносливости а_ш (рис. 13.12) или т_ш. Значения Таблица 13.4.
Материал. | Vo. | VT |
Малоуглеродистые стали. | 0,05. | 0,00. |
Среднеуглеродистые стали. | 0,10. | 0,05. |
Легированные стали. | 0,15. | 0,10. |
пределов ограниченной выносливости определяют по выражениям:

где Np и Л/д, — число циклов изменения нормальных и касательных напряжений; тп =* 9 для легированных сталей, подвергаемых упрочнению, т = 6 для углеродистых сталей.
Найденные пределы ограниченной выносливости должны соответствовать следующим значениям:
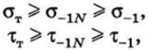
где ттиот — пределы текучести материала. При постоянстве передаваемого момента и частоты вращения независимо от числа реверсов число циклов изменения нормальных напряжений.
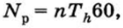
где п — частота вращения вала, об/мин; Th — ресурс работы механизма, ч. Для касательных напряжений ЛГЦН равно числу реверсов или включений механизма.
Амплитуда нормальных напряжений са и среднее напряжение цикла ст вычисляются по формулам.
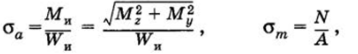
где Wu — момент сопротивления сечения изгибу; N — нормальная сила; А — площадь поперечного сечения. Для сплошного круглого сечения WH «0,Id3, для круглых сечений других видов значения WH определяются по формулам, приведенным в табл. 13.5.
Касательные напряжения для реверсивного механизма при равенстве вращающих моментов в одну и другую стороны изменяются по симметричному циклу.

где Wp — момент сопротивления сечения вала кручению. Для сплошного круглого сечения Wp * 0,2d3, в других случаях см. табл. 13.5. В нереверсивном механизме периодического дей;
Таблица 13.5.

Деформация и материал. | d, мм. | |||||||
Изгиб для углеродистых сталей, Kda | 0,95. | 0,92. | 0,88. | 0,85. | 0,81. | 0,76. | 0,7. | 0,61. |
Изгиб для легированных, Kd<5 и кручение для всех сталей, Kdx | 0,87. | 0,83. | 0,77. | 0,73. | 0,7. | 0,65. | 0,59. | 0,52. |
ствия касательные напряжения изменяются по отнулевому циклу: 
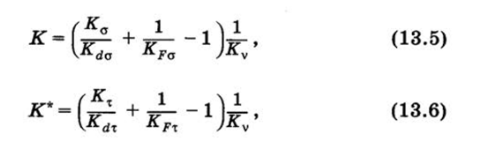
Коэффициенты снижения предела выносливости детали при расчете: на изгиб на кручение где Ка9 Кх — эффективные коэффициенты концентрации напряжений; KdG, Kdx — коэффициенты влияния абсолютных размеров детали (табл. 13.6); KFa, KFx — коэффициенты влияния шероховатости; Kv — коэффициент, учитывающий повы;
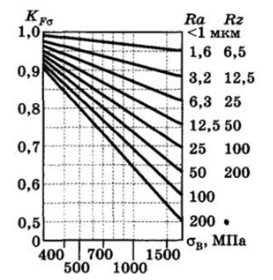
Рис. 13.13.
шение предела выносливости за счет технологического упрочнения поверхности детали (табл. 13.7). Значения коэффициентов концентрации напряжений для галтели приведены в табл. 13.8, для других концентраторов — в табл. 13.9. На рис. 13.13 приведен график зависимости коэффициента влияния шероховатости KFo от параметров шероховатости Яа и Яг. Значение KFx определяется по соотношению KFx = 0,575.йГ^о + + 0,425.
Обработка поверхности. | Для сердцевины св, МПа. | Коэффициент упрочнения Kv | ||
Гладкие валы. | Валы с концентрацией напряжений. | |||
ка = 1,5. | К0 = 1,8…2,0. | |||
Закалка с нагревом ТВЧ d = 10…20 мм. | 600…800 800…1000. |
| 1,6…1,7. | 2,4…2,8. |
Азотирование. | 900… 1200. | 1,1…1,25. | 1,5…1,7. | 1,7…2,1. |
Цементация. | 700…800 1000…1200. |
| 2,0. | —. |
Дробеструйный наклеп. d = 8…40 мм. | 600… 1500. | 1,1…1,25. | 1,5…1,6. | 1,7…2,1. |
Накатка роликом d = = 17…30 мм. | со т—< 1-^. | 1,3…1,5. | 1,6…2,0. | |
Лазерное упрочнение. | 800…1000. | 1,25…1,8. | 1,9…2,3. | 2,3…2,9. |
Ионное азотирование. | —. | 1,3…1,9. | 2…2,4. | 2,4…3. |
Таблица 13.8.
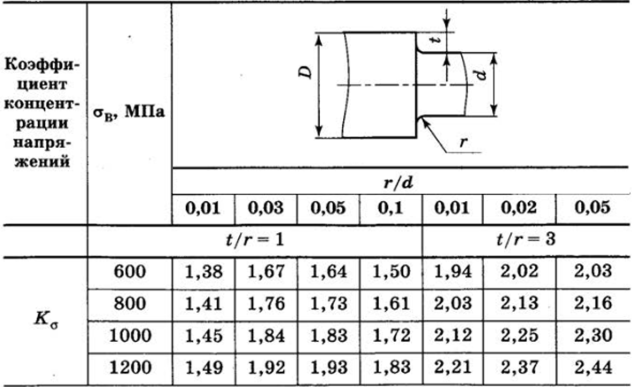
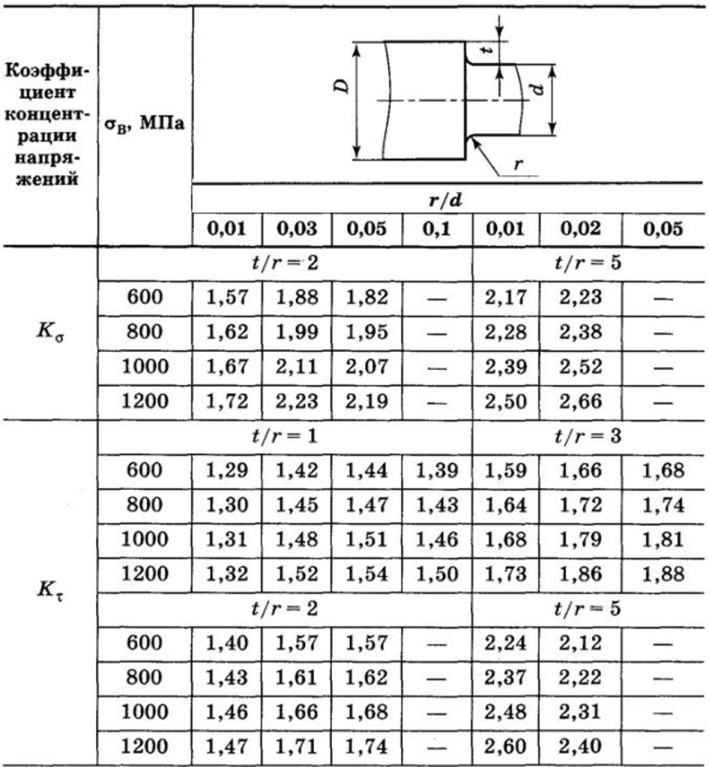
Таблица 13.9.
ав, МПа. | Шлицы. | Шпоночная канавка. | Резьба. | Поперечное отверстие диаметром. | |||
прямо; бочные. | эволь; вент; ные. | со ступенчатым выходом. | с плавным выходом. | d/D
| d/D
| ||
1,55. | 1,76. | 1,46. | 1,96. | 2,05. | 1,85. | ||
1,65. | 2,01. | 1,62. | 2,20. | 2,10. | 1,90. | ||
Шлицы. | Шпоночная канавка. | Поперечное отверстие. | |||||
ав, МПа. | Резьба. | диаметром. | |||||
прямо; бочные. | эволь; вент; ные. | со ступенчатым выходом. | с плавным выходом. | d/D
| d/D
| ||
1,72. | 2,26. | 1,77. | 2,61. | 2,20. | 2,00. | ||
1,75. | 2,50. | 1,92. | 2,90. | 2,30. | 2,10. | ||
*т.
2,36. | 1,46. | 1,54. | 1,54. | 1,80. | |
2,55. | 1,52. | 1,88. | 1,71. | 1,95. | |
2,70. | 1,58. | 2,22. | 2,22. | 1,98. | |
2,80. | 1,60. | 2,39. | 2,39. | 2,00. |
Расчет на статическую прочность. При действии больших пусковых моментов и при работе с кратковременными большими перегрузками валы механизмов общего машиностроения рассчитываются на статическую прочность по эквивалентным напряжениям. Поскольку напряжения от нормальных сил относительно малы, основными являются напряжения изгиба и кручения, эквивалентные напряжения определяются как 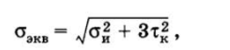
где си — наибольшие напряжения изгиба; тк — наибольшие напряжения кручения.
Для валов сплошного круглого поперечного сечения Wp = = 2 WH =" 0,2d3, и в этом случае.
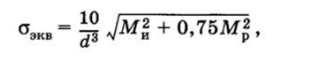
запас прочности по пределу текучести.
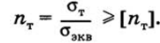
Допускаемый запас прочности принимается [ят].
* 1,2…1,8.
Расчеты валов на жесткость. Под действием поперечных нагрузок валы прогибаются, что вызывает перекос зубчатых колес, который может привести к защемлению Рис. 13.14 тел качения подшипников.
При высоких частотах вращения из-за эксцентриситета возникает опасность появления колебаний вала, вызывающих его увеличенные прогибы. В кинематических механизмах повышенные прогибы валов приводят к снижению точности их функционирования.
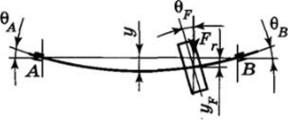
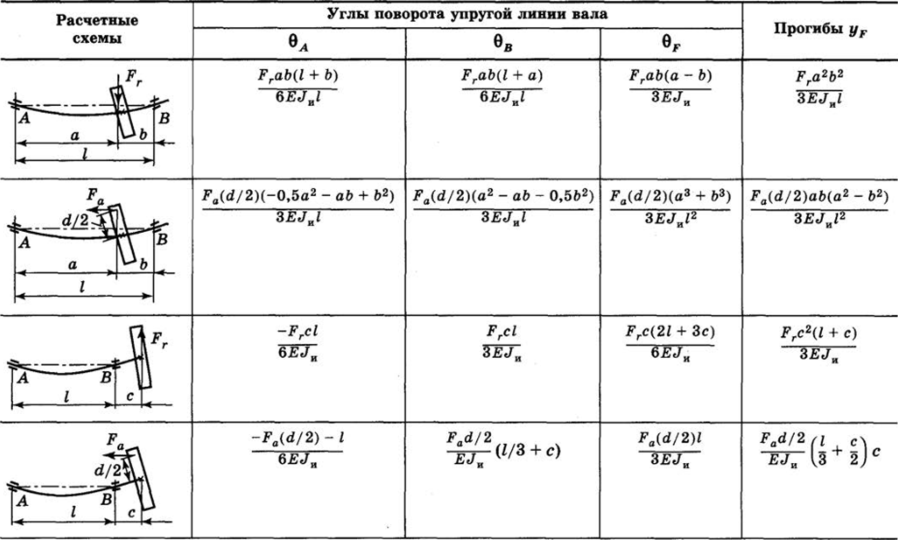
Изгибная жесткость валов оценивается стрелой прогиба у и углами наклона упругой линии вала 0А, 0B, 0F (рис. 13.14). Крутильная жесткость оценивается углом закручивания <�р. Жесткость валов проверяется условиями.

Расчет прогибов у и углов поворота 0 ведется методами, изложенными в курсе сопротивления материалов. Ориентировочно значения прогибов и углов поворота можно оценить по приближенным формулам табл. 13.10.
Увеличение жесткости и уменьшения прогибов валов получаются при смещении поперечной нагрузки от середины вала ближе к опорам.
В каждой конкретной конструкции прогибы валов зависят от диаметров валов, расположения нагрузки относительно опор. Допускаемые значения прогибов [z/] и углов поворота [0] в местах установки зубчатых колес и опор валов устанавливаются на основании статистических данных. Для обеспечения нормальной работы подшипников допускаемые значения углов поворотов [0] не должны превышать следующих величин: 0,005 рад в шарикоподшипниках; 0,05 рад в сферических подшипниках; 0,002 рад в роликовых подшипниках; 0,0005 рад в игольчатых подшипниках; 0,002 рад в подшипниках скольжения.
В зубчатых передачах величина прогиба определяется в зависимости от модуля зацепления т и типа передачи: [yF] < < 0,01m для цилиндрических передач; [у] < 0,005 т для конических, гипоидных и глобоидных передач. Угол наклона упругих линий валов в местах расположения зубчатых колес [в] < 0,001 рад. Максимальный прогиб вала z/max < [у] — * 0,0003/ (I — расстояние между опорами).
Крутильную жесткость валов оценивают сравнением угла закручивания <�р с его допускаемым значением.
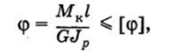
где Мк — крутящий момент; I — длина участка вала; G — модуль сдвига; Jр — полярный момент инерции сечения. Допускаемые значения углов закручивания для валов различного назначения могут значительно отличаться по величине. Например, для торсионных валов и соединительных рессор [<�р] не более 30° на 1 м длины, а в валиках приводов следящих систем — не более 15 с. Поэтому для конкретных валов допускаемые углы закручивания должны быть заданы в технических условиях или уточнены при натурных испытаниях.
Динамика валов рассматривается в гл. 5.
Пример конструирования и расчета промежуточного вала прямозубого цилиндрического редуктора на усталостную прочность Исходные данные:
- ? частота вращения вала п = 264 об/мин;
- ? расчетный вращающий момент с учетом Кд Т = = 106 400 Н • мм;
- ? делительный диаметр колеса dx = 180 мм;
- ? делительный диаметр шестерни d2 =76 мм, df2 = 66 мм;
- ? назначенный ресурс Th = 2000 ч;
- ? режим работы реверсивный, циклограмма нагружения показана на рис. 13.15, а (tx = t2 = 10 с);
- ? материал вала — сталь 12ХНЗА (ав = 950 МПа; от =700 МПа; а_! = 420 МПа);
- ? диапазон рабочих температур ±60 °С.
Проектировочный расчет.
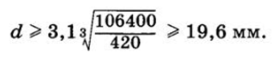
Диаметр вала определим по формуле (13.1), выбрав в соответствии с кинематической схемой для промежуточного вала с несимметричным расположением зубчатых колес k = = 3,1 (см. табл. 13.3) и приняв вал сплошным (с = 0, рис. 13.15, б):
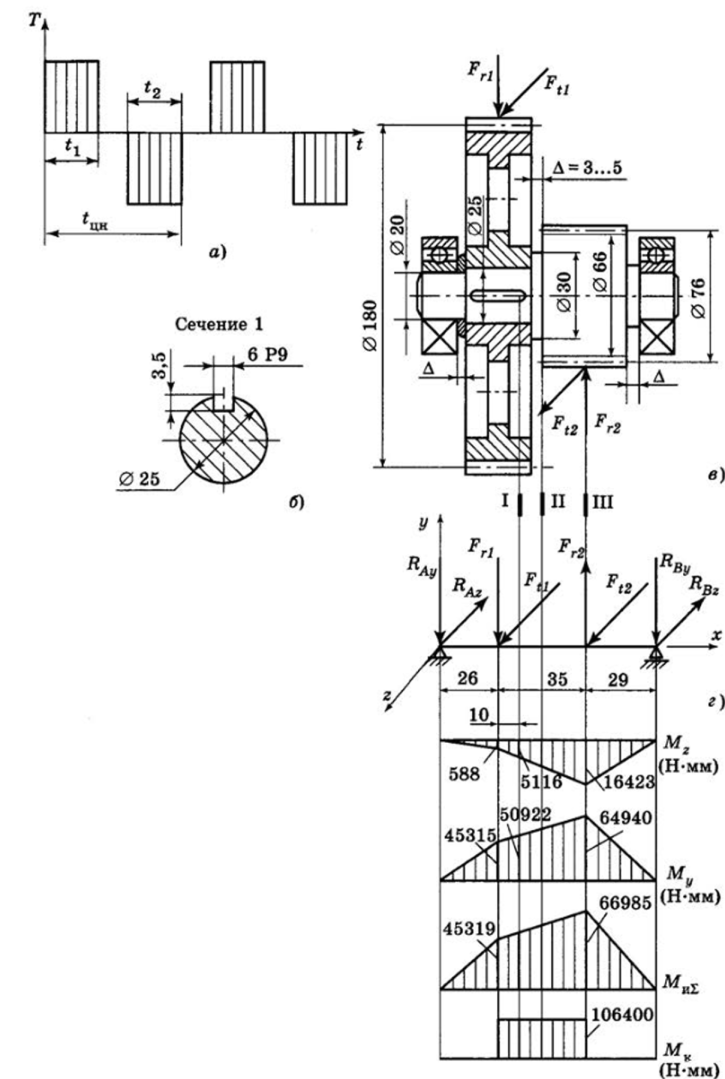
Рис. 13.15.

Конструирование вала. По найденному диаметру подбираем подшипники. Поскольку передача прямозубая цилиндрическая и осевые силы отсутствуют, выбираем шарикоподшипники радиальные легкой серии с внутренним диаметром d = = 20 мм. Вал будем выполнять ступенчатым, обеспечивающим удобную сборку и имеющим более равномерное распределение напряжений по его длине (рис. 13.15, в). Диаметр шестерни df2 = 66 мм немного превышает диаметр вала, и поэтому ее выполняем за одно целое с валом. Колесо большого диаметра делаем съемным. Между подшипниками и зубчатыми колесами должен быть обеспечен радиальный зазор Д, равный примерно половине толщины корпуса редуктора. Передача вращающего момента от зубчатого колеса к валу обеспечивается шпоночным соединением. Диаметр вала в месте соединения с зубчатым колесом принимаем несколько большим (d = = 25 мм), чем необходимо под подшипники. Длину вала в месте соединения с зубчатым колесом назначают в соответствии с длиной ступицы насаживаемой детали. Размеры призматической шпонки выбираем по ГОСТ 23 360–78. Для обеспечения осевой фиксации зубчатого колеса между его ступицей и внутренним кольцом подшипника устанавливаем промежуточную шайбу. С противоположной стороны ступица зубчатого колеса упирается в буртик на валу. В правой опоре для фиксации вала в осевом направлении также выполняем упорный буртик, в который упирается подшипник. Наружный диаметр промежуточной шайбы и диаметр упорного буртика должны быть менее наружного диаметра внутреннего кольца подшипника. Подшипники в корпусе устанавливаем так, чтобы исключить их осевое перемещение.
После конструктивной проработки вала выполняется проверочный расчет его на усталостную прочность.
Расчет вала на прочность. Расчет вала на усталостную прочность проводим в следующей последовательности.
- 1. Выбор расчетной схемы. Рассматриваем вал как балку, расположенную на двух опорах. Для радиальных подшипников опоры располагаем по центру тел качения (см. рис. 13.11).
- 2. Определение расчетных нагрузок, действующих в зацеплении зубчатых колес (рис. 13.15, г). Зубчатые колеса прямозубые цилиндрические, в зацеплении которых действуют окружные и радиальные силы:


Рассчитанные силы переносим на ось вала, как показано на рис. 13.15, г.
3. Построение эпюр изгибающих и крутящих моментов (рис. 13.15, д). Под действием найденных сил вал изгибается в плоскостях XOY и XOZ. Определим реакцию.
RX:

Крутящий момент передается от колеса к шестерне Мк = = 106 400 Н-мм.
Изгибающие моменты в плоскости XOZ:

На рис. 13.15, д приведены эпюры изгибающих моментов Му, MZJ суммарного изгибающего момента Ми1 и крутящего момента Мк.
4. Выбор расчетного (опасного) сечения. При расчете на усталостную прочность опасным является сечение с концентратором напряжений. В данном случае это сечения I и II. В сечении I концентратором напряжений является паз под шпонку. Это сечение смещено относительно середины зубчатого колеса в сторону увеличения изгибающих моментов до конца шпоночного паза. В сечении II концентратором напряжений является галтельный переход.
В сечении III, где действуют максимальные изгибающие моменты, диаметр вала в 2,64 раза больше, чем в сечении I, и, соответственно, моменты сопротивления изгибу и кручению в этом сечении в 2,643 выше, чем для сечения I. Следовательно, сечение III не является опасным.
Таким образом, в качестве расчетных должны быть рассмотрены сечения I и II.
5. Проверочный расчет вала по сечению /.
Значения изгибающих моментов в сечении I:

Напряжения кручения в расчетном сечении.
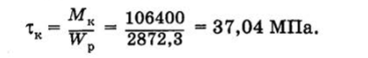
Момент сопротивления сечения кручению (см. табл. 13.5).
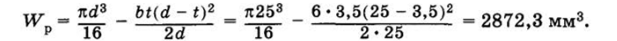
Нормальные силы на вал не действуют, и цикл изменения нормальных напряжений в этом случае симметричный оа = ои. Запас прочности по нормальным напряжениям.

Число циклов изменения нормальных напряжений Np — = nTh60 = 264 • 2000 • 60 «3,16 • 107 циклов больше базового числа циклов для сталей N0 = 107, поэтому в качестве предельных напряжений выбираем предел выносливости <�з_х = 420 МПа.
Коэффициент снижения предела выносливости детали 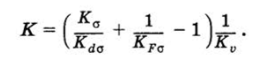
Эффективный коэффициент концентрации напряжений для сечения с пазом под шпонку (см. табл. 13.9) Ка = 2,2; масштабный коэффициент (см. табл. 13.6) Kdo *= 0,8; коэффициент, учитывающий шероховатость поверхности при 1,2 5 Л, а (см. рис. 13.13), KFa = 0,97; коэффициент, учитывающий поверхностное упрочнение, Kv = 1, так как вал не подвергался поверхностному упрочнению. Таким образом, имеем.

Значение запаса прочности по нормальным напряжениям.
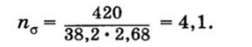
В реверсивном механизме при равных вращающих моментах цикл изменения касательных напряжений также симметричный, ха = тк, запас прочности.
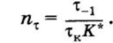
Число циклов изменения касательных напряжений в соответствии с циклограммой нагружения (см. рис. 13.15, а) 
Поскольку NUH = 3,6 • 105 меньше базового числа циклов для сталей N0 = 107, то в качестве предельных напряжений используется ограниченный предел выносливости т_1ЛГ, значение которого вычисляется по формуле.

где тт * 0,6от = 0,6 • 700 = 420 МПа — предел текучести при кручении; х_х * 0,6о ^ = 0,6 *420 = 252 МПа — предел выносливости при кручении. Таким образом, имеем 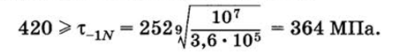
Коэффициент снижения предела выносливости детали при действии касательных напряжений.
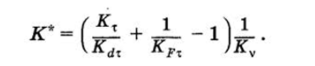
Эффективный коэффициент концентрации напряжений Кх = 2,14 (см. табл. 13.9); масштабный коэффициент Kdx = 0,8 (см. табл. 13.6); коэффициент, учитывающий шероховатость поверхности, KFx — 0,575KFa + 0,425 = 0,575*0,97 + 0,425 = = 0,98.
Таким образом,.
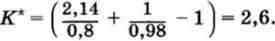
Запас прочности по касательным напряжениям.

Суммарный запас прочности.

Условие прочности выполняется.
Аналогичным образом проводится расчет по сечению И. Если условие прочности выполняется как в сечении I, так и в сечении II, то прочность вала обеспечивается.
Если рассчитанные запасы прочности значительно превышают допустимые значения, то для снижения массы конструкции вал можно сделать пустотелым, соблюдая условие прочности.