Плоские волны в проводящей среде

Для проводящей среды е = е₀р = р_гр₀, у «wea, поэтому к₂ = ДоруУравнение (5.1) при этом будет иметь вид.

Уравнение (5.5) представляет собой линейное дифференциальное уравнение второго порядка. Его решение запишется следующим образом:

где С_ь С₂ — постоянные интегрирования, это комплексы, они определяются из граничных условий и для каждой конкретной задачи свои; р = ±yJjoi[iу — корни характеристического уравнения.

Поскольку V7- Ve-'⁹⁰ = e^j45° = (1 + j) / [2, р можно представить еще и так:

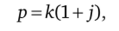
где к = л/соуц/2.

Напряженность электрического поля определим из уравнений Максвелла, при этом E=-rot Н.

У

Найдем.

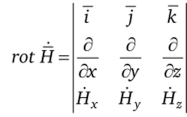
_п дН _п дН _п Yr.

В рассматриваемой задаче — = 0 и — = 0, поэтому выражение rot Н

дх ду

в значительной мере упрощается:

Следовательно,.

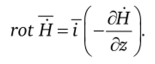
Производная.

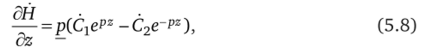
тогда Ё = р/ у (С₂е~Р² -Qe?²).

Выражение (5.7) показывает, что напряженность электрического поля в плоской волне при выбранном расположении осей координат направлена вдоль оси х, об этом свидетельствует присутствие единичного орта оси х (орта i). Таким образом, в плоской электромагнитной волне между векторами Ё и Н есть пространственный сдвиг в 90° (Е направлено по оси х, а Н по оси у).

Частное от деления р на у принято называть волновым сопротивлением и обозначать.

Волновое сопротивление измеряется в омах. Оно зависит от свойств среды (от у и р) и от угловой частоты со.

В соответствии с уравнением (5.8) проекция? на ось л: равна Ё = Ё_пад +Е_тр, где ?_пад =^c_C₂e~^pz и Ё_отр =-Z_cC_le>^{, z}

Проекция Н на ось у

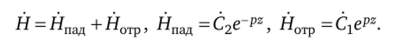
Составляющие падающей волны ?_пад и Я_пад дают вектор Пойнтинга П_пад (рис. 5.4, а). Он направлен вдоль положительного направления оси z. Следовательно, движение энергии с падающей волной происходит вдоль положительного направления оси z.

Составляющие отраженной волны ?_отр и Н_отр дают вектор Пойнтинга П_отр (рис. 5.4, б). Последний направлен вдоль отрицательного направления оси z. Это означает, что отраженная волна несет с собой энергию и движение энергии происходит вдоль отрицательного направления оси z.

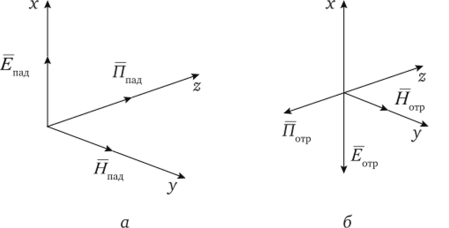
Рис. 5.4. Определение направления вектора Пойтинга:

a — падающая волна; 6 — отраженная волна Волновое сопротивление Z_c можно трактовать как отношение.

^пад /^пад •.

Поскольку волновое сопротивление является числом комплексным, то сдвиг во времени между ?_пад и Я_пад для одной и той же точки поля равен 45°.

Рассмотрим распространение плоской электромагнитной волны в однородной проводящей среде, простирающейся теоретически в бесконечность (рис. 5.5).

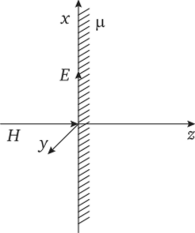
Рис. 5.5. Схема для анализа распространения электромагнитной волны в проводящей среде.

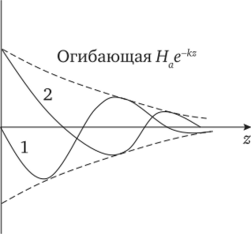
Рис. 5.6. График напряженности магнитного поля вдоль координаты z.

Электромагнитная волна проникает из диэлектрика в проводящую среду и распространяется в последней. Поскольку среда простирается теоретически в бесконечность и падающая волна в толще проводящей среды не встречает границы, которая «возмутила» бы ее распространение, отраженной волны в данном случае не возникает.

При наличии только одной падающей волны.

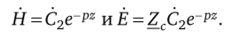
Постоянную интегрирования С₂ определим из граничных условий. Если обозначить напряженность магнитного поля на поверхности проводящей среды через Н_а = H_ae-'^v", то при z = О С₂ =Н_а.

Поэтому с учетом величины р получим.

В свою очередь,.

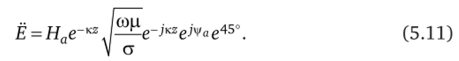
Можно записать выражения для мгновенных значений Я и Е. Для этого правые части уравнений (5.10) и (5.11) необходимо умножить на e>^(0t [2 и взять мнимые части от получившихся произведений. Получим.

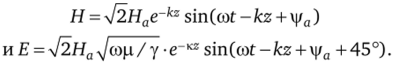
Проведем анализ полученных выражений. Амплитуда Я равна V2Я_ае^_/сг. Амплитуда Е равна Т2Я_аЛ/сор/у — е^-Ь. По мере увеличения z уменьшается множитель e~^kz. Следовательно, по мере проникновения электромагнитной волны в проводящую среду амплитуды Е и Я уменьшаются по показательному закону. На рис. 5.6 изображены огибающие амплитуд Я, построенные по уравнению H_ae~^kz. Мгновенное значение Я и Е определяется аргументом синуса. Аргумент синуса в последних выражениях зависит от z и от rot. Если принять rot = const и рассмотреть график мгновенных значений Я в функции от z, то будет получена кривая 1 (см. рис. 5.6) при rot + |/_а = 90°.

Для того чтобы охарактеризовать, насколько быстро уменьшается амплитуда падающей волны по мере проникновения волны в проводящую среду, вводят понятие «глубина проникновения».

Под глубиной проникновения Д понимают расстояние вдоль направления распространения волны (вдоль оси z), на котором амплитуда падающей волны Е (или Я) уменьшается в е = 2,7183 раз.

Уравнением для определения глубины проникновения является выражение e~^kl = е^-1. Отсюда следует, что /сД = 1 или Д = 1 /к.

Глубина проникновения зависит от свойств проводящей среды (у и р) и от частоты го. Так, если электромагнитная волна имеет частоту / = 5000 Гц и проникает в проводящую среду, у которой у = 10⁷ см/м и p_r = 10³, то.

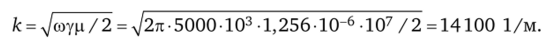
Глубина проникновения Д = 1 /к = 0,007 см, т. е. на ничтожном расстоянии (0,007 см) амплитуды Я и? уменьшились в 2,7183 раза.

Под длиной волны X в проводящей среде понимают расстояние вдоль направления распространения волны (вдоль оси z), на котором фаза колебания изменится на 2л. Длина волны определится из уравнения Хк = 2л, отсюда X = 2л/к.

Для рассмотренного числового примера.

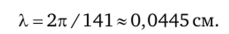
Иногда пользуются понятием «фазовая скорость» распространения электромагнитной волны в проводящей среде.

Под фазовой скоростью понимают скорость, с которой необходимо было бы перемещаться вдоль оси z, чтобы колебание имело одну и ту же фазу. Фаза колебания определяется выражением (rot — kz + |/_а). Производная от постоянной величины есть нуль, поэтому.

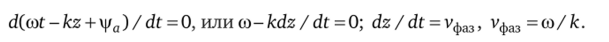
Для рассмотренного числового примера.

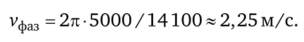
Таким образом, электромагнитная волна проникает в глубь проводящей среды с малой скоростью и на очень малую глубину.