Случай двух номинальных признаков

П3.4. Анализ таблиц сопряженности: представление

ПЗ.4.1. Построение концептуальных связей по статистическим данным

Для анализа связи между двумя номинальными признаками составляют так называемые таблицы сопряженности. Строки таблицы сопряженности соответствуют категориям одного признака, а столбцы — категориям другого признака. Элемент на пересечении строки и столбца — количество объектов, обладающих соответствующими категориями и того и другого признаков.

Рабочий пример 3.10. Таблица сопряженности на малых городах

Чтобы создать перекрестную классификацию двух признаков торговых городов, «Банки» («Ба») и «Фермерский рынок» («Фр»), необходимо прежде всего категоризовать количественный признак «Банки». Рассмотрим, например, разбиение на четыре категории в табл. 3.13.

Таблица 3.13

Определение категорий «Ба» по данным о торговых городах.

Эти категории перекрестно классифицируются с категориями «Есть» и «Нет» признака «Фр» в таблице сопряженности (табл. 3.14). Кроме численностей объектов в категориях перекрестной классификации, в таблице содержатся и суммарные численности категорий — в последних, добавленных, строке и столбце таблицы — вот почему их называют маргинальными. Общее число объектов — в правом нижнем углу таблицы.

Таблица 3.14.

Перекрестная классификация категорий «Ба» и «Фр».

Таблица 3.15

Относительные частоты для перекрестной классификации «Фр» / «Ба», %.

Те же значения сопряженности в относительных частотах (полученные делением на общее количество объектов) представлены в табл. 3.15.

Самостоятельная работа

• 3.10.1. Постройте таблицу сопряженности для признаков «Тип протокола» и «Тип атаки» по данным о компьютерных атаках (см. табл. 1.4) как в абсолютных численностях, так и в относительных частотах.
• 3.10.2. Разделите ирисы в табл. 1.2 на четыре группы по признаку «Длина чашелистика» и постройте таблицу сопряженности полученного номинального признака с разбиением по таксонам как в абсолютных численностях, так и в относительных частотах.

Таблица сопряженности может быть использована для исследования связи между отдельными категориями. Наибольшая связь — концептуальная (логическая) (рис. 3.20). Концептуальная связь усматривается тогда, когда в строке k все немаргинальные величины, кроме одной, скажем в столбце /, равны 0, что означает, что если объект имеет категорию к первого признака, он заведомо будет иметь категорию / второго признака. Это означает логическую импликацию, или концептуальную связь k => /.

Рис. 3.20. Нетривиальная импликация.

Вопрос 3.16. Постройте таблицу сопряженности для признаков «Тип протокола» и «Тип атаки» для данных о компьютерных атаках.

Ответ. См. табл. 3.16.

Таблица сопряженности на данных о компьютерных атаках.

Таблица 3.16

Рабочий пример 3.11. Импликации и эквивалентности по таблице сопряженности

Рассмотрим таблицу сопряженности признаков «Тип протокола» и «Тип атаки» по данным о компьютерных атаках (см. табл. 3.16). В строках Udp и Icmp табл. 3.16 только один ненулевой элемент. Это значит, что таблица содержит логические импликации Udp=>Normal и Icmp=>Smurf. Более того, в столбце Smurf тоже только один ненулевой элемент! Это значит, что согласно таблице категории Icmp и Smurf эквивалентны, т. е. Icmp Smurf.

Самостоятельная работа

• 3.11.1. Рассмотрите таблицу сопряженности признаков «Сектор экономики» и «Использование Интернета» но данным табл. 1.1. Можно ли сделать вывод о наличии логических импликаций согласно этой таблице?
• 3.11.2. Сформируйте из признака «Нас» в табл. 1.5 данных о малых городах Англии категоризованный признак «Величина поселения» с категориями «Малая» (до 2400 жителей), «Средняя» (больше 2400, но меньше 8500 жителей) и «Большая» (более 8500 жителей). Рассмотрите таблицу сопряженности этого нового признака и признака «Фр». Можно ли сделать вывод (-ы) о наличии логических импликаций согласно этой таблице?

Задание 3.6. Чистка таблицы сопряженности: лучше не делать.

К сожалению, в табл. 3.14 сопряженности признаков «Ба» и «Фр» нулей нет, т. е. нет смысла говорить о концептуальной связи каких-либо категорий этих признаков. Однако некоторые значения в таблице близки к 0, что подвергает нас соблазну немного почистить данные. Ценой удаления из выборки только двух городов мы можем добиться того, что в строке «Да» табл. 3.14 два последних значения станут 0, а не 1. Такое преобразование будет означать, что фермерский рынок может появиться только в городе с четырьмя и более банками. То есть логическое правило «Если Ба > 4, то в городе есть фермерский рынок» справедливо согласно модифицированной таблице сопряженности.

Воспользуемся этим приемом для усиления подмеченной корреляции путем очищения таблицы от малых значений. Поправленная таким образом табл. 3.14 преобразуется в табл. 3.17: удалено всего 13 городов из выборки, зато как хорошо проявлена концептуальная связь: «В городе есть фермерский рынок тогда и только тогда, когда число банков в нем больше 4»! Но нс будем забывать, что цена этого — 13 удаленных городов. Они составляют почти 30% исходной выборки.

Таблица 3.17^[1]

Очищенная перекрестная классификация «Ба» / «Фр» (удалено 13 городов).

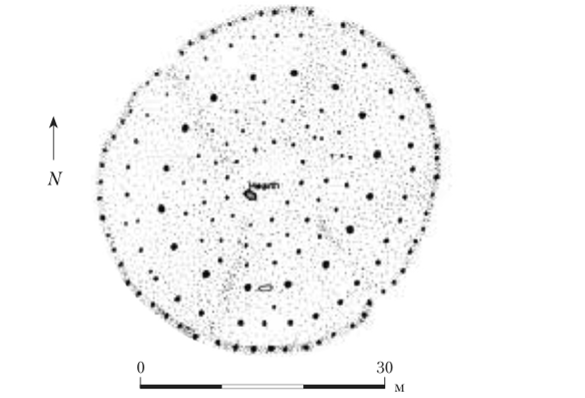
Рис. 3.21. Нехарактерные объекты.

Схема концентрических овалов, образуемых столбиками Вудхенджа, неолитического памятника в Южной Англии; несколько столбиков находятся вне овалов — что они и зачем они, неизвестно¹

Подобная поправка данных с удалением «нехарактерных» объектов, граничащая с мошенничеством, — одна из причин возникновения популярного парадоксального афоризма, приписываемого Б. Дизраэли, известному британскому политику XIX в.: «Есть три градации лжи: ложь, наглая ложь и статистика». Здесь мы касаемся проблемы, которая до сих пор не получила в анализе данных скольнибудь общего решения. Ясно, что в множестве данных может присутствовать некое, обычно не очень большое, число нехарактерных объектов, подчас «выбросов» по отношению к остальным данным, которые следует удалить до того, как анализировать эти данные (см., например, рис. 3.21). Но как их выявить? А если такие данные характеризуют вовсе не выбросы, а наоборот, новые возможности развития? Безотносительно к этой проблеме мы предпочитаем не очищать данные, а искать другие способы выявления концептуальных связей.

• [1] URL http://structuralarchaeology.blogspot.ru/2009/01/19-proper-study-of-mankind-is-postholes.html