Пример выполнения основных процедур факторного анализа

Итак, процедура определения нагрузок в факторном анализе состоит из двух этапов: сначала по выборочным значениям наблюдаемых переменных У находятся некоторые нагрузки L, позволяющие выписать конкретные уравнения (12.2) относительно факторов F, затем с помощью ортогонального преобразования нагрузок L и факторов F находятся такие нагрузки L и факторы F, которые обеспечивают описание наблюдаемых переменных Y уравнением (12.2) с наименьшим числом факторов.

Возможно, чаще всего используемым методом определения первого набора нагрузок на первом этапе является метод главных компонент. С помощью этого метода находятся значения нагрузок, которые дают оценку полной общности настолько близко, насколько возможно, к полной выборочной дисперсии. Ковариациями пренебрегается.

В табл. 12.3 представлены элементы факторной модели (для примера табл. 12.1), которые используются в методе главных компонент.

Таблица 123

Элементы метода главных компонент.

Переменная, Yj	Выборочная дисперсия, Sf	Общность On)2 + (/|2)2
Финансы, Y{
Маркетинг, У2
Право, У3
Сумма.

Напомним, что показатель общности является частью дисперсии переменной У, которая объясняется факторами. Чем больше эта часть, тем более успешна постулируемая факторная модель, как говорят, она лучше объясняет переменную. Метод главных компонент находит значения нагрузок 1ф которые приближают полную общность (T_t в табл. 12.3) настолько близко, насколько возможно, к сумме выборочных дисперсий переменных (Т₀ в табл. 12.3). Все основные статистические компьютерные пакеты программ реализуют метод главных компонент. Решение этим методом для примера табл. 12.1 показано в табл. 12.4.

Таблица 12.4

Решение методом главных компонент для данных табл. 12.1.

Оценки нагрузок обозначены символом чтобы отличать их от теоретических нагрузок Ijj. Точность, с которой приводятся значения, является чрезмерной для практики (два десятичных разряда были бы достаточными); это сделано, чтобы было легче ориентироваться при сравнении с результатами других компьютерных программ. Последние числа в столбцах (3) и (4) означают суммы квадратов нагрузок.

Как очевидно, решение получилось достаточно точным. Нагрузки на F являются относительно большими для У), но близки к нулю для У₂ и У₃. Нагрузки на F₂ близки к нулю для У, но относительно высоки для У₂ и У₃. Таким образом, фактор Т, мог интерпретироваться как соответствующий математическим способностям, a F₂ — как соответствующий гуманитарным способностям. Заметим, что факторная модель объясняет почти 100, 99,7 и 99,2% выборочных дисперсий оценок по финансам, маркетингу и праву соответственно. В целом эти два фактора объясняют 99,78% суммы всех выборочных дисперсий.

Сумма квадратов нагрузок на может интерпретироваться как вклад F_i и сумма квадратов нагрузок на  — как вклад Р₂ в объяснение суммы выборочных дисперсий. В табл. 12.4.

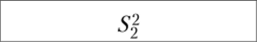
Таким образом, /', объясняет около 9,873/17,92 или 55,1%, a F₂ — около 44,7% суммы выборочных дисперсий.

Оценка частной дисперсии У, |/, — это разность между выборочной дисперсией и оценкой общности У; (табл. 12.5).

Таблица 12.5

Оценка частной дисперсии для данных таблицы 12.1.

Приближение полной общности насколько возможно к сумме выборочных дисперсий (придавая одинаковый вес каждой переменной) имеет смысл, когда переменные У, измеряются в одинаковых единицах, как в примере этой главы. Однако когда это нс так, ясно, что метод главных компонент благоприятствует переменным с большими дисперсиями за счет переменных с малыми дисперсиями.

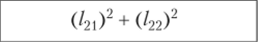
Поэтому общепринято стандартизировать переменные до обработки их методом главных компонент так, чтобы средние значения всех переменных были нулевыми и дисперсии — равными единице. Это достигается вычитанием из каждого наблюдения Y_j} (/-го наблюдения переменной У,), среднего (У_;) и делением результата на среднее квадратическое отклонение (стандартное отклонение) 5, переменной, чтобы получить стандартизованное наблюдение. Заметим, что Y_t — это оценка параметра р, из уравнения (12.2).

Можно показать, что ковариации стандартизованных наблюдений Y_i} равны коэффициентам корреляции исходных наблюдений (дисперсии стандартизованных наблюдений Y_jjt конечно, равны 1). Этот последний результат может быть легко проверен с использованием данных табл. 12.1. Сначала вычисляются числовые характеристики:

Затем наблюдения преобразуются к стандартному виду Y_tJ

Например, j-e наблюдение переменной У, вычисляется по формуле.

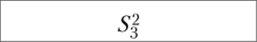
Можно убедиться, что среднее стандартизованных наблюдений равно нулю, а их дисперсии и стандартные отклонения равны единице. Ковариация переменных У₍ и У₂ равна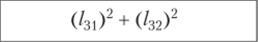

Коэффициент корреляции У_х и У₂равен.

и равен ковариации стандартизованных переменных У_х и У₂:

Корреляционная матрица исходных переменных (равная матрице ковариации стандартизованных переменных) получается следующей:

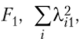
В общем случае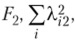

Решение методом главных компонент для стандартизованных переменных необязательно будет совпадать с решением для нестандартизованных переменных. В некоторых статистических программах (например, SPSS, 5Л5), стандартизация и метод главных компонент — опции по умолчанию. В табл. 12.4 приведены данные решения методом главных компонент для нестандартизованных переменных. Для стандартизованных переменных решение будет выглядеть несколько иначе. Оно приведено в табл. 12.6.

Таблица 12.6

Решение методом главных компонент для стандартизованных переменных табл. 12.1.

Как и в случае с исходными нестандартизованными наблюдаемыми переменными, оценки по маркетингу и праву зависят от одного общего фактора F_x с нагрузками 0,9941 и 0,9961 соответственно (F_x может интерпретироваться как гуманитарные способности), по практически не зависят существенно от другого фактора Д₂ ^с нагрузкой 0,2 987 (математические способности); обратное имеет место для оценок по финансам. Однако в отличие от случая нестандартизованных переменных гуманитарные способности влияют сильнее, чем математические способности: Т составляет 1,981 463/3, или приблизительно 66%, в то время как // составляет 1,8 306/3, или приблизительно 33,6% суммы выборочных дисперсий. Эти два фактора вместе объясняют 2,98 977/3, или 99,659%, суммы выборочных дисперсий стандартизированных переменных, немного меньше, чем для исходных нестандартизированных наблюдаемых переменных (там было 99,783%).

Когда решение на первом этапе не обеспечивает ожидаемую структуру нагрузок, выполняется второй этап факторного анализа, на котором применяется вращение фактора, чтобы найти другой набор нагрузок, который приспосабливает наблюдения так же хорошо, но лучше интерпретируется. Поскольку невозможно рассмотреть все такие вращения, используют вращения, удовлетворяющие определенным критериям.

Возможно, чаще других используется критерий варимакс (varimax). Согласно этому критерию с помощью вращения находятся нагрузки, которые максимизируют дисперсии квадратов нагрузок на каждый фактор; цель состоит в том, чтобы сделать некоторые из этих нагрузок как можно больше, а другие — как можно меньше по абсолютной величине.

Результат применения метода варимакс к первому набору нагрузок, представленному в табл. 12.6, приведен в табл. 12.7.

Таблица 12.7

Решение с помощью вращения методом варимакс для стандартизованных переменных табл. 12.1.

Оценки показателя общности каждой переменной и полного показателя общности являются такими же, как в табл. 12.6, но нагрузки на факторы немного отличаются. В этом примере вращение практически не изменило первые оценки нагрузок и пропорции сумм выборочных дисперсий, объясняемых этими двумя факторами.

Другой критерий — квартимакс (quartimax) стремится максимизировать дисперсии квадратов нагрузок для каждой переменной и имеет тенденцию находить факторы с высокими нагрузками для всех переменных.

В рассмотренном примере количество факторов и их характер предполагались заданными. Было разумно предположить, что только гуманитарные и математические способности могут быть двумя факторами, влияющими на изучение дисциплин и оценку. Однако в некоторых других ситуациях используемое число факторов и их интерпретация не всегда очевидны. В этом случае чаще всего осуществляется перебор числа факторов (1,2,…) до получения удовлетворительного результата.

Заметим также, что существует определенная субъективность в признании нагрузок большими или близкими к нулю по абсолютной величине. Это приводит к разногласию относительно того, поддерживается ли предполагавшаяся структура нагрузок при наблюдаемой выборке переменных или нет.

Также должно приниматься во внимание, что существуют и другие методы получения первого и последующих решений для нагрузок и факторов, и каждая комбинация первого решения и метода вращения могут привести к существенно различным интерпретациям.

До появления быстродействующих компьютеров значительные усилия были посвящены нахождению приближенных решений проблемы, особенно в оценке показателей общности другими средствами, что упрощало бы проблему, приводя к известной сокращенной матрице корреляции. Это затем использовалось для определения факторов и нагрузок. С появлением быстродействующих компьютеров проблема минимизации решается быстро и непосредственно, и показатели общности вычисляются в процессе решения, вместо того чтобы вычисляться заранее. Алгоритм MinRes (MINimum RESidual — минимальный остаток) особенно подходит для решения этой задачи и является едва ли не единственным средством обнаружения точного решения. MinRes — рекуррентный метод численного решения несимметричной системы линейных уравнений, который приближает решение в векторном подпространстве Крылова с минимальным остатком (предложен К. Пэйджем и М. Сондерсом в 1975 г.).