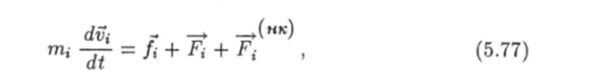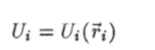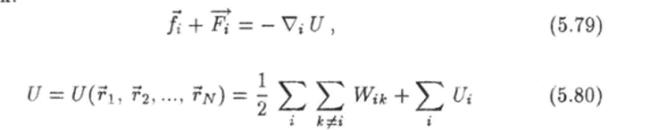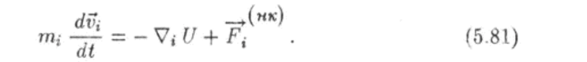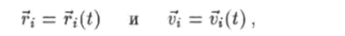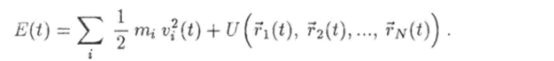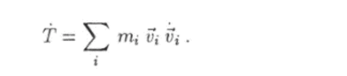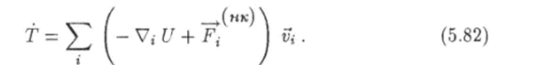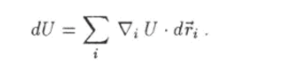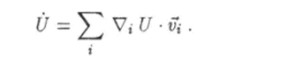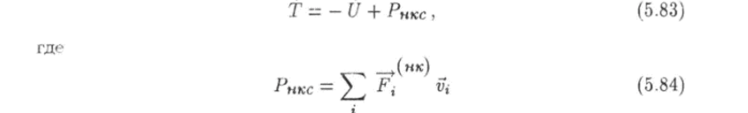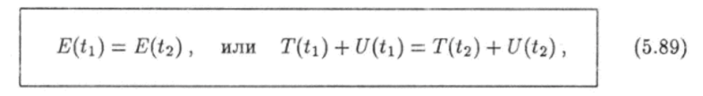Закон сохранения энергии

В общем случае на каждую частицу исследуемой системы действуют и внутренние, и внешние силы; и консервативные, и неконсервативные. С учетом сказанного запишем второй закон Ньютона для i-й частицы в виде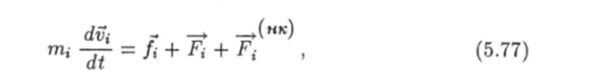

где fi и Fi — действующие на эту частицу внутренняя и внешняя консервативные силы соответственно; - внутренние и внешние не консервативные силы вместе взятые.

Внешняя консервативная сила F,-, которая действует на частицу с номером 7, по определению равна.

где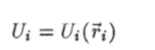

— потенциальная энергия i-й частицы во внешнем силовом поле.

Используя формулы (5.67) и (5.78), консервативную силу можно представить та**.

где.

— потенциальная энергия системы частиц. Подставив выражение (5.79) ь уравнение (5.77), получим:

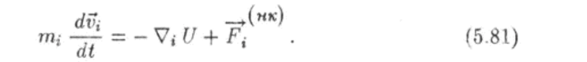
Полная механическая энергия системы равна сумме кинетических и потенциальных энергий входящих в систему частиц:

— кинетическая энергия системы частиц. При движении частиц, когда их радиус-векторы и скорости изменяются с течением времени:

энергия системы также, вообще говоря, изменяется со временем:

Найдем закон изменения полной механической энергии системы частиц с течением времени. Для этого вычислим производную по времени от этой функции. Сначала, используя результаты, полученные в разделе 4.5, запишем выражение для производной по времени от кинетической энергии: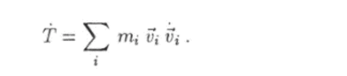

С учетом уравнений движения (5.81) будем иметь.

Дифференциал потенциальной энергии (5.80) по определению (4.35) равен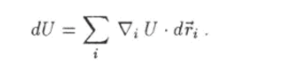

Разделив это равенство на бесконечно малое приращение времени dt, найдем производную по времени от потенциальной энергии системы:

При помощи этой формулы преобразуем равенство (5.82) к виду.

есть мощность неконсервативных сил. Из равенства (5.84) следует, что.

т.е. производная от полной механической энергии системы по времени равна мощности внутренних и внешних неконсервативных сил. Равенству (5.85) можно придать вид.

— элементарная работа неконсервативных сил. Проинтегрировав обе части равенства (5.86) по времени в пределах от до *2> получим:

где.

где.

— приращение полной энергии системы за время от t до.

— работа, совершенная за это время неконсервативными силами.

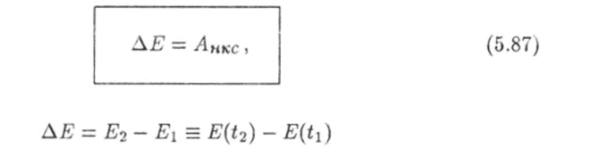
Следствием равенства (5.85) является закон сохранения полной энергии системы частиц. Если мощность неконсервативных сил, действующих на частицы системы, равна нулю в течение некоторого времени, то полная механическая энергия системы в это время не изменяется:

Из равенства (5.87) следует, что полная механическая энергия E (t) системы в момент времени t будет равна энергии E (t2) системы в момент времени $ь если работа неконсервативных сил за это время равна нулю:

при условии.