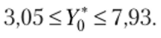Нахождение доверительного интервала для условного математического ожидания

Так же как и для парной регрессии, для условного математического ожидания M (Y Х₀) при уровне значимости, а доверительный интервал имеет вид.

где У₀ — значение объясняемой переменной Y при значении вектора объясняющих переменных Х₀; S_M — стандартная ошибка точечного прогноза для условного математического ожидания M (Y Х₀); ?_кр = t_a._v — критическое значение статистики Стьюдента.

Значение S_M определяется как.

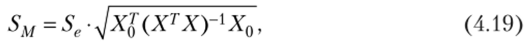
где S_e — стандартная ошибка регрессии; Х₀ — значение вектора объясняющих переменных, для которого ищется доверительный интервал.

В отличие от парной линейной регрессии, где S_M зависит только от одной объясняющей переменной, для множественной регрессии оценка S_M зависит уже от вектора Х₀, что существенно усложняет геометрическую интерпретацию интервальной оценки.

Интервальная оценка для индивидуальных значений зависимой переменной

Построенная оценка (4.18) определяет интервал возможных значений математического ожидания M (Y | Х₀), но не отдельных возможных значений (называемых индивидуальными значениями и обозначаемых у* или I⁷*) переменной У, которые отклоняются от М (У | Х₀).

Интервальная оценка для индивидуальных значений У* с доверительной вероятностью у имеет вид.

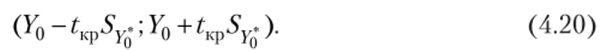
Дисперсия индивидуального значения случайной величины У* определяется выражением.

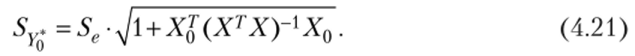
Появление единицы под знаком корня по сравнению с формулой (4.19) объясняется учетом дополнительного отклонения значений У* от своего математического ожидания М (У | Х₀).

Замечание 4.3. В литературе прогнозирование по модели множественной регрессии обычно подразумевает нахождение доверительного интервала по формулам (4.20) и (4.21).

Пример 4.6.

Имеются данные по некоторому региону зависимости ВВП У от основных фондов Х_{ и оборотного капитала Х₂ (табл. 4.6).

Таблица 4.6

Исходные данные к примеру 4.6.

Предполагая, что между переменными У, Х_ЬХ₂ существует линейная зависимость, найдем выражение этой зависимости и интервальные оценки для условного математического ожидания (среднего значения) М (У Х₀) и индивидуального значения У* при слсдущих значениях для Х Х_х = 8 и Х₂ = 6. Доверительная вероятность у = 0,95.

Решение. 1. Обозначим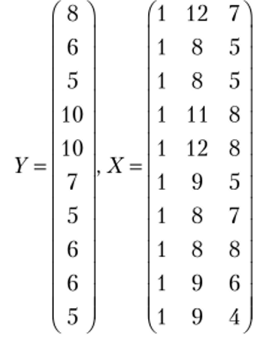

и вычислим следующие величины:

• матрицу произведения X⁷ и X

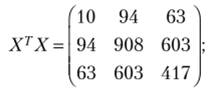
• вектор XTY

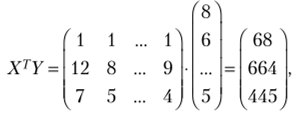
содержащий три проекции;

• обратную матрицу.

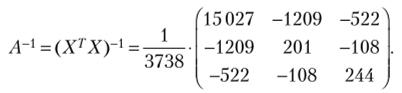
Вычислим вектор коэффициентов уравнения регрессии:

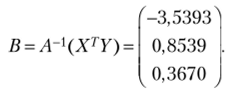
Построенное уравнение линейной множественной регрессии имеет вид.

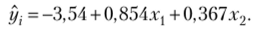
2. По условию задачи необходимо оценить M (Y Х₀) при XI= (1 8 6). Такой оценкой является значение регрессии, вычисленное для заданного вектора X: Х_{ = 8 и Х₂ = 6.

Произведем оценку S_e полученного уравнения регрессии. Для этого по уравнению регрессии вычислим все расчетные значения, найдем разности е, и е}. Результаты представлены в табл. 4.7.

Таблица 4.7

Результаты расчетов к примеру 4.6.

Вычисляем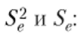

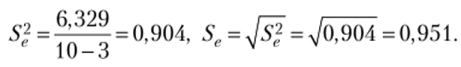
Рассчитываем значение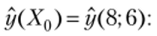

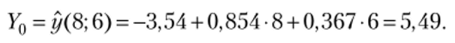
Матрица-столбец заданного вектора —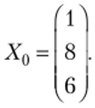

Для нахождения S_M и вычислим.

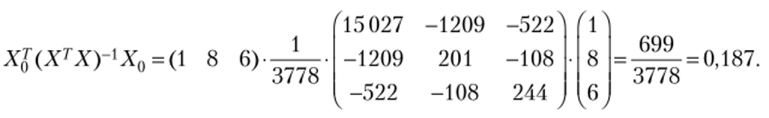
Теперь по формуле (4.19).

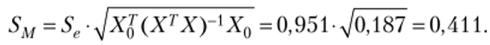
Величина статистики Стыодента /(0,95; 10 — 3) = 2,36. Интервальные оценки среднего значения с доверительной вероятностью у = 0,95 определяются по формуле (4.18):

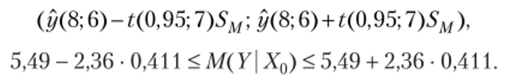
Таким образом, интервальные оценки для среднего значения M (Y | Х₀): 4,52 < ₀) < 6,46.

3. Теперь найдем доверительный интервал для индивидуального значения У при тех же значениях Х_{ = 8 и Х₂ = б.

Вычислим дисперсию индивидуального значения по формуле (4.21):

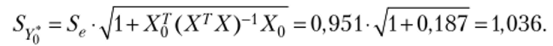
Интервальная оценка для индивидуального значения У определяется, но формуле (4.20):

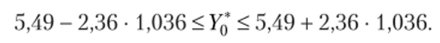
С доверительной вероятностью у = 0,95 выполняется неравенство