Устранение автокорреляции случайных составляющих

Как говорилось в самом начале главы, основной причиной наличия случайного члена в модели являются несовершенные знания о причинах и взаимосвязях, определяющих то или иное значение зависимой переменной. Поэтому свойства случайных отклонений, в том числе и автокорреляция, в первую очередь зависят от выбора математической модели уравнения регрессии и состава объясняющих переменных. Чаще всего автокорреляция вызывается неправильной спецификацией модели, поэтому необходимо прежде всего скорректировать саму модель. Если все разумные процедуры изменения спецификации модели исчерпаны, а автокорреляция имеет место, то можно предположить, что она обусловлена какими-то внутренними свойствами ряда остатков {e_t}. В этом случае можно воспользоваться авторегрессионным преобразованием. Обычно наиболее целесообразным и простым преобразованием является авторегрессионная схема первого порядка AR ( 1).

Рассмотрим модель парной линейной регрессии.

Тогда наблюдениям t и (t — 1) соответствуют формулы и.

Пусть случайные отклонения подвержены воздействию авторегрессии первого порядка = pe_r_₁ + v_v где v_t — случайные отклонения, удовлетворяющие всем предпосылкам МНК, а коэффициент р известен. Вычтем из равенства (6.8) соотношение (6.9), умноженное на р:

где

Так как по предположению коэффициент р известен, то очевидно, что у*, х*_п Pq, v_t вычисляются достаточно просто. В силу того что случайные отклонения v_t удовлетворяют предпосылкам МНК, оценки Pq и Pj будут обладать свойствами наилучших линейных несмещенных оценок.

Рассмотренное авторегрессионное преобразование может быть обобщено на любое число объясняющих переменных, следовательно, применимо для устранения автокорреляции во множественном уравнении линейной регрессии.

На практике значение коэффициента р обычно неизвестно, и его необходимо оценивать. Существует ряд методов оценивания этого коэффициента. Приведем некоторые из них.

Определение р на основе статистики Дарбина — Уотсона. В качестве оценки коэффициента р может быть взят коэффициент корреляции т_ее =1-DW/2. Этот метод оценивания дает хорошие результаты при большом числе наблюдений. В этом случае оценка r_{ee j} коэффициента р будет достаточно точной.

Метод Хилдрета — Лу. По данному методу регрессия у* =(3q +Р, х_г* +v_t оценивается для каждого возможного значения р из отрезка [-1; 1] с любым шагом (например, 0,001; 0,01 и т. д.). Величина, дающая наименьшую стандартную ошибку регрессии, принимается в качестве оценки коэффициента р. Значения и Ь_{ оцениваются из уравнения регрессии с данным значением р. Этот итерационный метод широко используется в пакетах компьютерных прикладных программ.

Метод первых разностей. Метод можно использовать в том случае, когда есть основание считать, что автокорреляция отклонений очень велика. Для временных рядов обычно характерна положительная автокорреляция остатков р > 0. Поэтому при высокой автокорреляции полагают р = 1, и уравнение регрессии принимает вид

Обозначив 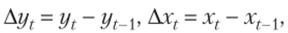получим.

Коэффициент Ь_{ оценивается обычным МНК. Коэффициент доопределяется из соотношения

Замечание 6.2. Метод первых разностей предполагает слишком сильное упрощение (р = ±1). Поэтому более предпочтительными являются итерационные методы.

Пример 6.4.

Определим наличие автокорреляции по данным, приведенным в табл. 6.7, и устраним автокорреляцию, используя модель парной линейной регрессии и авторегрессионную схему первого порядка AR ( 1) (определение р произведем на основе статистики Дарбина — Уотсона).

Таблица 6.7

Исходные данные для примера 6.4.

Решение. По МЫК находим уравнение регрессии: у_х = -9,416 + 1,197 д,-.

1. Графический метод. Строим зависимость остатков от номера наблюдения (табл. 6.8, столбец 5).

Результаты представлены на рис. 6.7. График зависимости отклонений e_t от номера наблюдений i говорит о положительном характере автокорреляции, т. е. с увеличением номера наблюдения разброс с, увеличивается. Наблюдается волнообразное поведение отклонений e_v

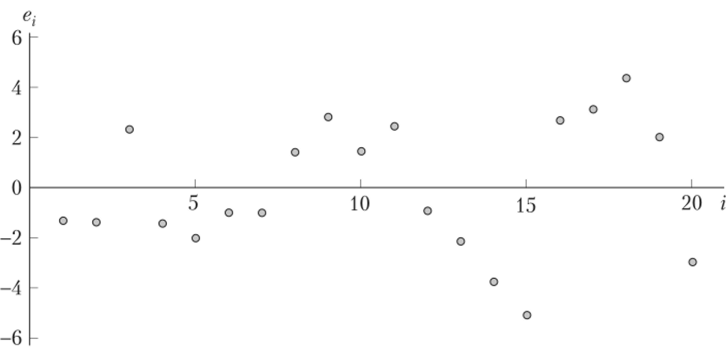
Рис. 6.7. Графический метод для примера 6.4.

2. Проверка, но методу рядов.

Вычисляем все значения у_х по уравнению регрессии и находим разности е_х = у, — у, (см. табл. 6.8, столбцы 4 и 5). Подсчитываем количество знаков «плюс», «минус» и число рядов к: п = 20, п_л = 9, п₂ = 11, к = 7. Для у = 0,95 из статистических таблиц находим к_х = 6 и к₂ = 16. Так как наше значение к попадает в промежуток 6 < к = 7 < 16, автокорреляция по методу рядов не обнаружена.

Таблица 6.8

Вычисления к примеру 6.4.

3. Проверка по критерию Дарбина — Уотсона.

Заполняем столбцы 6—8 табл. 6.8. Из каждого значения в 5-м столбце вычитаем предыдущее значение и результат заносим в 6-й столбец. Подсчитываем квадраты остатков и квадраты разностей (7-й и 8-й столбцы).

Статистика Дарбина — Уотсона:

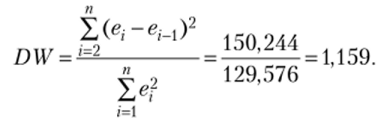
Для п = 20, т = 1 (число объясняющих параметров), у = 0,95 по статистическим таблицам Дарбина — Уотсона находим d_L = 1,201 и d_v = 1,411. Так как DW < d_L, это свидетельствует о положительной автокорреляции остатков.

Замечание 6.3. Если хотя бы один из методов показал наличие автокорреляции, гипотеза об отсутствии автокорреляции отвергается.

4. Устранение автокорреляции.

Используем авторегрессонную схему первого порядка AR ( 1). Вместо переменных .г, у рассмотрим новые переменные х", у , значения которых вычисляются по следующему правилу:

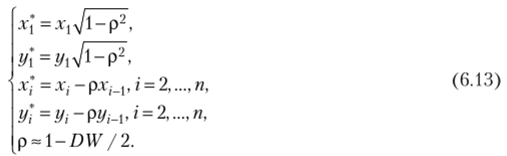
Пусть Ь'_й = />₀(1 — р). Коэффициент 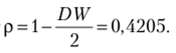С помощью обычного МНК по переменным х* и у* оцениваем коэффициенты уравнения 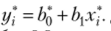Далее находим Ь₀ =Ь$ / (1 — р). Результаты вычислений приведены в табл. 6.9.

Устранение автокорреляции к примеру 6.4.

Таблица 6.9

Определенные по МНК значения /;, = 1,219, = -6,653. Значение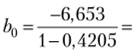

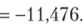
Полученное уравнение регрессии у₍-_нов =—11,476 + 1,219*₍ (сравните с первоначальным уравнением регрессии у, =-9,416+1,197*,-).

Пример 6.5.

Определим наличие автокорреляции по данным, приведенным в табл. 6.10, и устраним автокорреляцию, используя модель парной линейной регрессии и авторегрессионную схему первого порядка Л7?(1) (определение р произведем на основе статистики Дарбина — Уотсона).

Таблица 6.10

Исходные данные для примера 6.5.

По MI1K находим уравнение регрессии:=4,732−0,788*,.

1. Проверка по методу рядов.

Вычисляем все значения у, по уравнению регрессии и находим разности е, = у, — у, (см. табл. 6.11, столбцы 4 и 5). Подсчитываем количество знаков «плюс», «минус» и число рядов к п = 25, щ = 12, п₂ = 13, к = 16. Для у = 0,95 из статистических таблиц находим /г, = 8 и к₂ =19. Так как наше значение к попадает в промежуток 8 < к = 16 < 19, автокорреляция по методу рядов не обнаружена.

Таблица 6.11

Вычисления к примеру 6.5.

2. Проверка по критерию Дарбина — Уотсона.

Заполняем столбцы 6—8 табл. 6.11. Из каждого значения в 5-м столбце вычитаем предыдущее значение и результат заносим в 6-й столбец. Подсчитываем квадраты остатков и квадраты разностей (7-й и 8-й столбцы).

Статистика Дарбина — Уотсона:

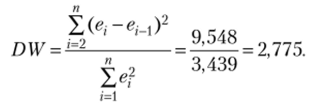
Для п = 25, т = 1 (число объясняющих параметров), у = 0,95 но статистическим таблицам Дарбина — Уотсона находим d_L = 1,29 и d_v= 1,45. Так как DW> 4 — d_Utэто свидетельствует об отрицательной автокорреляции остатков (см. рис. 6.3).

4. Устранение автокорреляции.

Используем авторегрессионную схему первого порядка ЛR (). Вместо переменных х, у рассмотрим новые переменные х*> у*, значения которых вычисляются по правилу (6.13).

Пусть 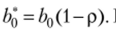Коэффициент 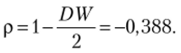С помощью обычного МНК.

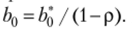
по переменным х* и у* оцениваем коэффициенты уравнения у] = + Ь_{х*. Далее находим Результаты вычислений приведены в табл. 6.12.

Таблица 6.12

Устранение автокорреляции к примеру 6.5.

Определенные по МНК значения Ь, = -0,02, Ъ'₀=3,608. Значение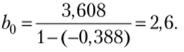

Полученное уравнение регрессии у, _мо" =2,6−0,02х₍ (сравните с первоначальным уравнением регрессии у-, =4,732−0,788х,).

Проверка нового уравнения регрессии по методу Дарбина — Уотсона показала DW = 1,594. Это свидетельствует об устранении автокорреляции остатков первого порядка.

Пример 6.6.

Определим наличие автокорреляции по данным, приведенным в табл. 6.13, и устраним автокорреляцию, используя модель множественной линейной регрессии и авторегрессионную схему первого порядка AR (1) (определение р произведем на основе статистики Дарбина — Уотсона).

Таблица 6.13

Исходные данные для примера 6.6.

По МНК находим уравнение регрессии:

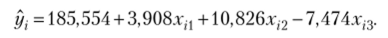
1. Проверка по методу рядов.

Вычисляем все значения у, по уравнению регрессии и находим разности е, = у, — у, (табл. 6.14, столбцы 6 и 7). Подсчитываем количество знаков «плюс», «минус» и число рядов к: п = 20, щ = 9, п₂ = 11, к = 8. Для у = 0,95 из статистических таблиц находим (| = 6и (₂ = 16. Так как наше значение к попадает в промежуток 6 < /.

Таблица 6.14

Вычисления к примеру 6.6.

2. Проверка по критерию Дарбина — Уотсона.

Заполняем столбцы 8 и 9 табл. 6.14 (подсчитываем квадраты остатков и квадраты разностей).

Статистика Дарбина — Уотсона.

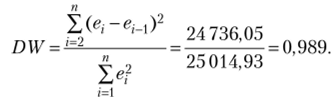
Для п = 20, т = 3 (число объясняющих параметров), у = 0,95 по статистическим таблицам Дарбина — Уотсона находим d_L = 1,0 и dy= 1,68. Так как DW< d_L, это свидетельствует об автокорреляции остатков.

3. Устранение автокорреляции.

Используем авторегрессонную схему первого порядка AR ( 1). Вместо переменных Xjj, у, рассмотрим новые переменные х1, у], значения которых вычисляются по формулам (6.12) и приведены в габл. 6.15. Значение р определяем по статистике DW: р = 0,505.

Таблица 6.15

Преобразование переменных.

Уравнение регрессии, полученное по новым переменным (п = 20):

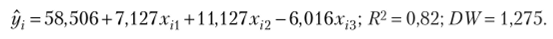
Уравнение регрессии, полученное по новым переменным без первого наблюдения (п = 19):

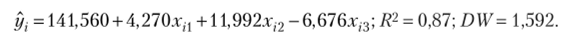
Ответ. В обоих случаях автокорреляция первого порядка не обнаружена.

• [1] Замечание 6.4. При большом числе наблюдений, как в примере 6.6,допускается опускать первое наблюдение. При малом числе наблюдений (меньше 10) первое наблюдение исключать нельзя.
• [2] 2 2 В силу ряда причин в регрессионных моделях может иметь место корреляционная зависимость между соседними случайными отклонениями. Этонарушает одну из фундаментальных предпосылок МНК. Вследствие этогооценки коэффициентов регрессии, полученные на основе МНК, перестаютбыть эффективными. Последнее делает ненадежными выводы как по значимости коэффициентов регрессии, так и по качеству самого уравнения. Поэтому достаточно важным является умение определить наличие автокорреляции. Существует несколько методов определения автокорреляции, среди которых были выделены графический метод, метод рядов, критерийДарбина — Уотсона. При установлении автокорреляции необходимо в первую очередь проанализировать правильность спецификации модели. Если после ряда возможных усовершенствований регрессии автокорреляция по-прежнемуимеет место, то, возможно, это связано с внутренними свойствами рядаотклонений. В этом случае возможны некоторые преобразования, устраняющие автокорреляцию. Среди них выделяется авторегрессионная схемапервого порядка Л/?(1). Для применения указанных схем необходимо оценить коэффициент корреляции между отклонениями. Это может бытьсделано различными методами: на основе статистики Дарбина — Уотсона, Хилдрета — Лу и др.