Математическая теория информации

Математическая теория информации трактует информацию в качестве абстрактного понятия. Считается, что единственное определение информации, которое не вызвало открытых возражений в научном сообществе, принадлежит отцу кибернетики, математику Норберту Винеру (1894- 1964), который в 1948 г. сформулировал максимально общее определение: «информация есть информация, а не материя и не энергия»". Из этого определения вытекает, что информация — не существующий реально объект, а умственная абстракция, созданная человеческим разумом.

В этом же смысле понятие информации используется в теории коммуникации, развитой в конце 1940;х гг. американским математиком Клодом Шенноном. В этой теории понятие информации служит для решения практических задач, с которыми сталкиваются инженеры-связисты: оптимизация кодирования сообщений, повышение помехоустойчивости, распознавание сигналов на фоне шумов, расчет пропускной способности каналов связи и т. п.

Каждому сигналу или их ансамблю (например, букве или слову), которые передаются по коммуникационному каналу, на основе известных статистических частот приписывалась априорная вероятность их появления. Считалось, что чем менее вероятно (т.е. чем более неожиданно), появление того или иного сигнала, тем больше информации для потребителя несет этот сигнал. Можно найти содержательные основания для подобной трактовки в обыденном понимании информации как новости или известия. Удобство вероятностно-статистического представления коммуникационной деятельности состоит в том, что можно ввести количественную меру для оценки степени «неожиданности» сообщения. В простейшем случае формула информации К. Шеннона имеет следующий вид:

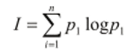
где / — количество информации, р, — вероятность появления /-го сигнала, п — количество возможных сигналов.^[1][2]

вид: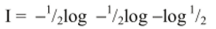

В случае двоичных логарифмов log ½ = -1, а I получается равным 1. Это значение принято в теории Шеннона в качестве единицы измерения информации и называется бит.

Отсюда проистекает понимание информации как снятой неопределенности или как результата выбора из возможных альтернатив. Есть другие математические концепции, не связывающие информацию с вероятностью. Например, в алгоритмической теории информации А.Н. Колмогорова информация — это длина алгоритма, позволяющего преобразовать один объект в другой, т. е. информация — это мера сложности объекта.

Ограниченность математических теорий информации заключается в том, что они полностью абстрагируются от осмысленности и ценности информации для потребителя. Критика данного подхода связана с тем, что в математических теориях понятие информации не связано ни с формой, ни с содержанием сообщений (сигналов), передаваемых по каналу связи. Получается, что «совокупность 100 букв, выбранных случайным образом, фраза в 100 букв из газеты, из пьесы Шекспира или теоремы Эйнштейна имеют в точности одинаковое количество информации"'.

Итак, согласно математической теории, информация, точнее количество информации, есть абстрактная фикция, умственный конструкт; она не существует в физической реальности, как не существуют логарифмы или мнимые числа.

• [1] Обзор концепций подготовлен на основе следующих работ: Соколов А. В. Общаятеория социальной коммуникации: Учебное пособие. СПб., 2002. С. 319 — 354;Информатика как наука об информации, информационный, документальный, технологический, экономический, социальный и организационный аспекты / Под ред.Р. С. Гиляревского. М., 2006. С. 12 — 42.
• [2] Винер И. Кибернетика или управление и связь в животном и в машине. 2-е изд. М., 1968. С. 201.