Теорема о максимальном потоке и минимальном разрезе

Пусть в ориентированной сети S = (N, U) от источника к стоку протекает поток, величина которого равна V. Поскольку пропускная способность каждой дуги c (i, j) является величиной конечной, то максимальная величина допустимого потока всей сети тоже ограничена. Максимальный поток сети определяется на основе одного из основных понятий теории сетей — понятия разреза. Введем понятие разреза.

Множество вершин N сети S = (N, U) можно разбить на два непересекающихся подмножества N_p и N_p, которые соединяются между собой дугами, образующими множество дуг разреза U_p. Причем исток s принадлежит множеству вершин N_p, а сток t принадлежит множеству вершин N_p. Тогда величина потока из множества N_p в множество N_p, протекающего по дугам и_р, не может быть больше, чем сумма пропускных способностей дуг этого множества, что можно записать.

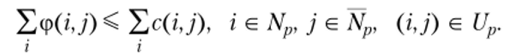
Этот барьер для потока, отделяющий множество вершин N_p от множества вершин N_p, называется разрезом и обозначается (N_p, N_p). Разрез представляет такое множество дуг U_p, исключение которых отделяет вход от выхода сети и, следовательно, отделяет множество N_p от N_p сети S — (N, U) таким образом, что существование потока в таком случае невозможно, и тогда V = 0. Причем начало дуги разреза принадлежит множеству N_p, а конец — N_p. Таким образом, в разрез входят дуги, соединяющие вершины этих множеств.

Величина максимального потока от источника s к стоку t ограничена сверху величиной разреза C (N_p, N_p), определяемой суммой пропускных способностей всех входящих в него дуг множества U_py и, следовательно, V < C (N_p, N_p). Минимальным разрезом сети называется разрез, имеющий минимальную величину.

В соответствии с теоремой о максимальном потоке и минимальном разрезе, сформулированной Фордом и Фалкерсоном, величина максимального потока У_тах от входа s (источника) в выход t (сток) равна величине минимального разреза, отделяющего вход и выход сети, и, следовательно,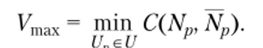

Рассматриваемые сети являются сетями с ограниченной пропускной способностью и имеют распространение в реальной жизни. Это послужило поводом к появлению и постановке задач о максимальном потоке разной природы, связанных с определением максимально допустимой величины V при соблюдении условий, записанных в виде системы уравнений и неравенств.

В сформулированной выше задаче для сохранения потока автомобилей (см. рис. 4.10), например, через перекресток (3) необходимо, чтобы поступающие потоки автомобилей к этой вершине (3) (р (1, 3) и ф (2, 3) равнялись величине потока, вытекающего из этой вершины ср (3, 4), что можно записать.

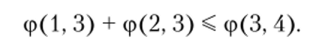
Аналогичные уравнения можно записать для остальных вершин сети. Поскольку задача заключается в определении максимально возможного потока в сети, то необходимо последовательно вычислить потоки через все разрезы и выбрать из них минимальный.

Разрез АА на рис. 4.10 отделяет источник (1) от стока (4), в данном случае вершину (4) от остальных вершин (1, 2, 3). Величина разреза определяется пропускной способностью входящих в него дуг (2, 4) и (3, 4) и соответственно равна С (2, 4) + С (3, 4) = 2 + 8 = 10. Затем можно определить все другие возможные варианты разрезов (В, В), (Д D) и (С, С). Тогда величина максимального потока от источника к стоку равна величине минимального разреза.

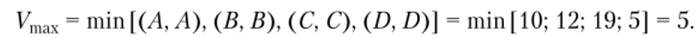
Приведенный вариант анализа фрагмента сети автомагистрали указывает на возможность применения приведенного принципа сохранения потока в коммерческой деятельности. Это позволит своевременно принимать оптимальные управленческие решения и облегчить оперативное вмешательство по регулированию не только автомобильных, по и финансовых или товарных потоков.

Пример 4.1. Построим разрезы для ориентированной сети, представленные на рис. 4.12, для различных множеств N_p:

• 1) N_p = {s, 1, 4,}, тогда N_p = {2, 3, t), следовательно, дуги разреза U_p = {(s, -3); (1, 3); (1, 2); (4, 0} (см. рис. 4.12), таким образом, С = = (N_p, NA = 10 + 4 + 3 + 9 = 26;
• 2) N_p = {s, 3}, тогда N_p = {1, 2, 4, t), следовательно, дуги разреза Up = {(5, 1); (3, 4);J3, 2)} (рис. 4.13), где величина разреза 14, таким образом, С = (N_p, Np) = = 5 + 7 + 2 = 14.

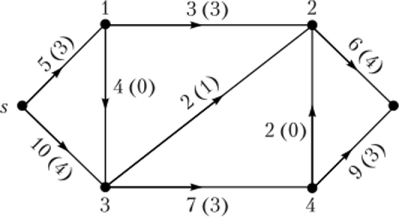
Рис. 4.12

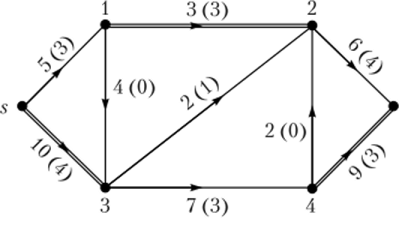
Рис. 4.13.

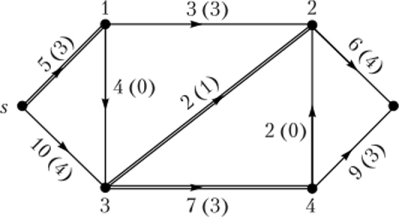
Па рисунках дуги разрезов выделены. Из рисунков очевидно, что после удаления дуг разрезов перестают существовать пути движения потока от входа сети s к выходу t. Разрезы имеют различные пропускные способности. Разрез, имеющий минимальную пропускную способность, будет минимальным разрезом сети.

Рис. 4.14

Рассмотренные алгоритм и примеры моделирования позволяют решать аналогичные по своей природе задачи, например по бесперебойному снабжению потоками электричества, бензина, газа, мазута, нефти, воды, продовольственными и непродовольственными товарами населенных пунктов, и таким образом предупредить появление критических ситуаций в городах и поселках нашей страны.