Дополнительный раздел. 
Теория игр

В этом параграфе мы обсудим две концепции, представляющие собой определенную альтернативу концепции равновесия по Нэшу, — рационализуемость (rationalizability) и многоуровневую рефлексию (level-к reasoning), а также понятие фокальной точки. Все эти подходы связаны с вопросом об общем знании в игре.

Концепция рационализуемости возникла из рассмотрения следующего вопроса. Пусть игра разыгрывается единственный раз, нет истории предыдущего разыгрывания и нет предварительных переговоров игроков. Что тогда можно сказать о разумных для игроков действиях, если рациональность всех игроков является общим знанием? Здесь речь не идет о равновесии, а лишь о логике выбора из первоначального набора стратеги й.

Рассмотрим игру со следующей двойной матрицей:

Зададимся вопросом: какие стратегии логично выбирать первому игроку? Вопрос осложняется тем, что первый игрок не знает точно, что сыграет второй игрок. Первый игрок может иметь различные представления (веры, beliefs) относительно действий второго игрока. Так, первый игрок может быть уверен, что второй игрок выберет свою первую чистую стратегию. Тогда первому игроку логично в ответ выбрать свою первую чистую стратегию. Аналогично при представлениях, что второй игрок выберет свою вторую чистую стратегию, первый игрок должен выбирать свою третью чистую стратегию.

Более интересный случай связан с тем, что первый игрок может быть не уверен, как именно сыграет второй игрок, и приписывать выбору вторым игроком своей первой чистой стратегии вероятность х и, соответственно, выбору второй стратегии — вероятность (1 — х). Последняя ситуация похожа на выбор вторым игроком смешанной стратегии, но в данном случае нас интересует не механизм, в соответствии с которым второй игрок может выбирать действие в игре, а неуверенность первого игрока относительно действий второго. Легко заметить, что, если х < —, то первому игроку разумно выорать свою первую чистую стратегию; если х = —, то первый игрок может выбрать первую или третью чистую стратегию, или смешанную, в которой.

только эти две стратегии входят в носитель; а если х > —, то первому игроку разумно выбрать свою третью чистую стратегию. Но вторая чистая стратегия ни при каких представлениях не будет для первого игрока наилучшей с точки зрения ожидаемого выигрыша. В этом смысле объяснить выбор первым игроком второй чистой стратегии затруднительно.

Основное предположение концепции рационализуемости состоит в том, что рациональный игрок не будет применять стратегию, не являющуюся для него наилучшей ни при каких представлениях о действиях других игроков. Другими словами, игрок не будет играть стратегию, никогда не являющуюся наилучшим ответом. Более того, так как рациональность игроков является общим знанием, другие игроки должны иметь представления, при которых они ожидают выбор такой стратегии с вероятностью нуль. Наконец, если при ограничениях на представления игроков какая-то из их чистых стратегий окажется никогда не наилучшим ответом, то игроки не должны такую стратегию выбирать, а другие должны ожидать ее выбор с нулевой вероятностью, и т. д.

Так, в нашем примере, поскольку рациональный первый игрок не должен выбирать свою вторую чистую стратегию, второй игрок должен иметь представления, в соответствии с которыми выбор данной стратегии ожидается с нулевой вероятностью. В этом случае для второго игрока вторая стратегия никогда не является наилучшим ответом. Тогда первый игрок должен ожидать ее выбор с вероятностью нуль. В этом случае для первого игрока его третья чистая стратегия никогда не является наилучшим ответом. В результате единственной рационализуемой стратегией для первого игрока является его первая чистая стратегия, а для второго — его первая чистая стратегия.

В нашем примере логика выбора рационализуемых стратегий совпадает с логикой последовательного исключения строго доминируемых стратегий, а полученный результат — с равновесием по доминированию. Это неслучайно. Приведем следующее утверждение (без доказательства)^[1].

Утверждение 2.13. Множество рационализуемых стратегий в игре двух лиц совпадает с множеством стратегий, оставшихся после последовательного исключения строго доминируемых стратегий.

Тогда с технической точки зрения не важно, какую из двух концепций использовать. Но содержательно подходы строгого доминирования и объяснимое™ различаются. В первом случае постулируется, что игрок не должен играть заведомо худшую стратегию. Во втором случае постулируется, что игрок должен иметь представления о действиях других игроков и выбирать лучшую стратегию в соответствии со своими представлениями в ответ. Уже для трех игроков подходы могут давать различный результат, что демонстрирует следующий пример — игра, в которой множество рационализуемых стратегий не совпадает с множеством стратегий, оставшихся после последовательного исключения строго доминируемых стратегий.

Пример 2.15 (несовпадение множеств стратегий)^[2]. Пусть задана игра грех лиц, в которой чистым стратегиям первого игрока соответствуют строки таблиц, чистым стратегиям второго игрока — столбцы таблиц, а чистым стратегиям третьего игрока — разные таблицы (в таблицах приведены только выигрыши третьего игрока):

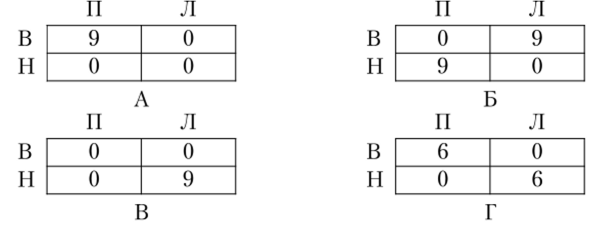
Здесь чистая стратегия Г не является строго доминируемой для третьего игрока, но не является и рационализуемой, т. е. не максимизирует выигрыш третьего игрока ни при каких представлениях о действиях первого и второго игроков.

То, что стратегия Г не является строго доминируемой, достаточно очевидно. Она могла бы доминироваться только смесью стратегий, А и В, но тогда и А, и В должны играться с вероятностями больше —, что одновре;

О менно невозможно.

Сложнее показать, что Г никогда не является наилучшим ответом. Обозначим х — представления третьего игрока о вероятности выбора первым игроком своей стратегии В, у — представления третьего игрока о вероятности выбора вторым игроком своей стратегии П. Тогда для того, чтобы стратегия Г была наилучшим ответом при некоторых представлениях третьего игрока, должна выполняться следующая система неравенств:

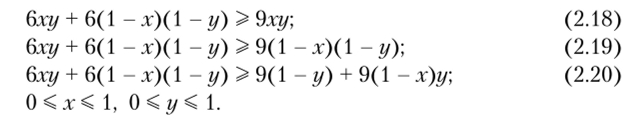
Покажем, что эта система несовместна. После преобразований можно получить, что неравенство (2.20) выполняется, если выполняются условия.

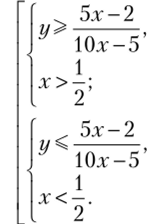
Решим первую систему из полученной совокупности совместно с неравенством (2.18), а вторую — с неравенством (2.19):

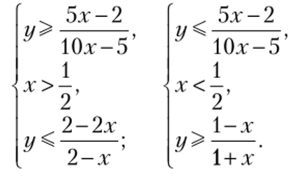
Для того чтобы соответствующие системы имели решения, необходимо, чтобы для некоторых х выполнялись неравенства (при условии, что знаменатели всех дробей положительны).

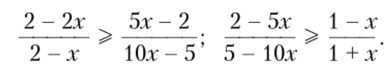
Легко проверить, что эти неравенства не выполняются ни при каких х. Следовательно, исходная система несовместна и стратегия Г не является наилучшим ответом ни при каких представлениях третьего игрока.

Что можно сказать о существовании рационализуемых стратегий в игре? Справедливо следующее утверждение (которое приводится без доказательства).

Утверждение 2.14. Множество рационализуемых стратегий в любой игре не пусто и содержит хотя бы одну чистую стратегию для каждого игрока.

Следовательно, любая игра может быть решена с использованием концепции рационализуемости, но для многих игр множество рационализуемых стратегий игроков слишком велико, чтобы говорить о точном предсказании разыгрывания. При этом в равновесии по Нэшу игроки, очевидно, выбирают рационализуемые стратегии, так как они выбирают наилучший ответ на фактические стратегии оппонентов. Является ли концепция равновесия по Нэшу слишком ограничивающей выбор игроков? Да, возможно, в однократной игре, особенно при наличии в ней нескольких равновесий по Нэшу, мы можем ожидать даже от рациональных игроков выбор стратегий, являющихся рационализуемыми, но не образующих равновесия по Нэшу.

Вторая концепция, которую мы рассмотрим в данном параграфе, — многоуровневая рефлексия — еще более радикально отличается от подхода равновесия по Нэшу, но тоже использует понятие наилучшего ответа. При этом происходит отказ от предпосылки общего знания рациональности и допускается возможность присутствия нерациональных игроков. Мы рассмотрим данный подход на примере из статьи [6].

Пример 2.16 (игра 11—20). Пусть два игрока играют в следующую игру. Каждый из них называет целое число от 11 до 20. В результате каждый получает число единиц полезности (в экспериментах — денежных единиц), которое он назвал. Плюс, если игрок назвал число ровно на единицу меньше оппонента, он получает 20 дополнительных единиц полезности.

Легко проверить, что в этой игре нет равновесий по Нэшу в чистых стратегиях. Хорошим упражнением для читателя может быть нахождение симметричного (существуют и несимметричные) равновесия в смешанных стратегиях (подсказка: должна ли стратегия «называть 20» выбираться с положительной вероятностью в симметричном равновесии?).

Стартовой точкой при анализе игры с точки зрения многоуровневой рефлексии является определение стратегии, логичной с точки зрения субъекта, не принимающего во внимание действия другого игрока. О таком субъекте говорят, что он обладает нулевым рангом (уровнем) рефлексии. В нашей игре, если не пытаться строить предположения о другом игроке, логичной выглядит стратегия «назвать 20».

Следующий уровень рефлексии можно получить, если игрок предполагает, что с большой вероятностью (или с вероятностью 1) его оппонент имеет нулевой ранг. Тогда игрок выберет наилучший ответ на стратегию игрока с рангом нуль. В нашем примере это стратегия «назвать 19». Значит, от игроков с первым рангом рефлексии мы ожидаем этот выбор.

Процесс можно продолжать — каждый следующий ранг рефлексии выбирает наилучший ответ на стратегию, соответствующую предыдущему рангу. В нашем примере игра устроена так, что игроки с девятым рангом выберут 11, с десятым — 20, и круг замкнется.

Логика подхода многоуровневой рефлексии состоит в том, что мы можем по данным о фактическом разыгрывании различных игр в экспериментах определить доли в популяции игроков с разным уровнем рефлексии, чтобы потом давать предсказания о разыгрывании различных игр этой популяцией. Сторонники данного подхода утверждают, что их предпосылки анализа более схожи с процессом принятия решения реальными людьми и статистически описывают данные лучше, чем концепция рациональных игроков, выбирающих равновесие по Нэшу.

Таким образом, исследовательская программа при применении подхода многоуровневой рефлексии состоит в следующем: определить стратегии, которые должны выбирать игроки с разным уровнем рефлексии, провести эксперимент, оценить доли игроков с разным уровнем рефлексии в популяции. Полученные оценки могут использоваться, например, для предсказания разыгрывания игр.

Сложности с применением подхода многоуровневой рефлексии возникают в следующих случаях. В некоторых играх нетривиально, что должен выбрать игрок с нулевым уровнем рефлексии (в частности, как в примере 2.4). В некоторых играх если игрок уже не считает, что все остальные игроки относятся к предыдущему уровню, а лишь что большинство относится к этому уровню, то его наилучший ответ существенно меняется. Так, в нашей игре, если игрок десятого уровня считает, что с 0,8 его оппонент имеет девятый тип (и выберет 11), а с вероятностью 0,2 — что его оппонент имеет первый тип (и выберет 19), то ему выгоднее выбирать уже не 20, а 18 в ответ. Иногда наилучшие ответы игроков разных уровней рефлексии совпадают, тогда их невозможно разделить в данных эксперимента. Но это обычно случается для высоких уровней рефлексии, а результаты экспериментов показывают, что число субъектов с уровнем рефлексии выше третьего очень мало. Наконец, когда выигрыши в экспериментах отождествляются с чисто денежной их составляющей, возможны ошибки из-за недостаточного учета влияния прочих факторов (в том числе и отношения к риску) на поведение испытуемых.

Концепция многоуровневой рефлексии привлекательна возможностью практической проверки и тем, что существенно ослабляет весьма строгие требования, которые предъявляются к рациональности игроков при определении равновесия по Нэшу.

В заключении упомянем о таком термине, как фокальная точка. Здесь речь идет не об особой концепции решения, а лишь о выборе из нескольких равновесий по Нэшу в играх координации.

В играх координации игрокам выгодно скоординировать свои действия (как в примере 2.4). Рассмотрим простой пример. Пусть три игрока — Алексей, Борис и Василий — играют в следующую игру. Они независимо друг от друга пишут на листе имена игроков в произвольном порядке. Если порядок имен у всех игроков совпадает, то тот, чье имя у всех на первой позиции, получает 300 ед. полезности, тот, чье имя на второй позиции, — 200 ед., тот, чье имя на третьей позиции, — 100 ед. Если порядок имен не совпадает у всех троих, то все получают по 0 ед. полезности. Тогда даже если мы играем за Василия, то приходится смириться и писать имена в алфавитном порядке. Здесь мы наблюдаем ситуацию, в которой действия игроков определяются нс только выигрышами, но и культурным контекстом, тем традиционным способом анализа ситуаций, который знают игроки и, что не менее важно, который является общим знанием, т.с. игроки знают, что и другие игроки знают, и т. д.

Фокальная точка — это профиль стратегий игроков, в котором каждый из игроков действует «общепринятым» способом, как в нашем примере. Строгого определения здесь дать не удается. Концептуально важно здесь то, что описание игры в нормальной форме может не включать важных элементов контекста, оказывающих влияние на поведение игроков.

• [1] Доказательство можно найти, например, в работе [11, с. 51—52].
• [2] Пример взят из работы [11].