Отношения между множествами и их элементами

В математике между различными математическим объектами могут устанавливаться различные отношения. Например, между двумя действительными числами может быть установлено отношение сравнения по величине, между двумя прямыми в пространстве отношение параллельности или перпендикулярности. В теории множеств также говорят о возможности установления различных отношений между рассматриваемыми объектами. Что же это за отношения?

Во-первых, можно устанавливать отношение между отдельным элементом и множеством. Мы уже об этом говорили, это отношение принадлежности. Элемент может принадлежать или не принадлежать данному множеству.

Например, если задано множество А = {1, 3, 9}, то 3 е А, а 10? А.

Во-вторых, отношения можно установить и между двумя множествами. Первое из этих отношений называется отношением включения.

Определение 2.1. Говорят, что множество В включается в множество А и пишут В с Л, если каждый элемент множества В является элементом множества Л. В этом случае множество В называется подмножеством множества Л.

Пример 2.2.

Рассмотрим две диаграммы Эйлера — Венна (рис. 2.3).

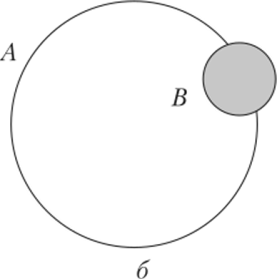
Рис. 2.3. Иллюстрация отношения включения.

На рис. 2.3, а изображено множество В, которое является подмножеством множества Л, так как каждый элемент В является и элементом А. На рис. 2.3, 6 В не является подмножеством А, так как в В есть элементы, которые не принадлежат Л. Записывают это так В (X А.

Можно привести и другой пример. Пусть даны множества М = {2, 3, 4, 5, 6} и N= {2, 6}. Ясно, чтоЛГсМ. Это можно записать и как М э N (читают: множество М содержит множество N).

Здесь целесообразно обратить внимание на то, что множество для другого множества может являться подмножеством или элементом. Например, для множества М= {2, 4, 6, 8, 10} числа 4 и 6 являются элементами этого множества, они связаны с множество М отношением принадлежности: 4 е М, 6 е М. С другой стороны, {4} с М, так же как и {6} с М.

Пустое множество является подмножеством любого множества: 0 с Л.

Докажем это утверждение методом от противного. Предположим, что пустое множество не является подмножеством произвольного множества Л. Тогда найдется такой элемент#, который пустому множеству принадлежит, а множеству Л не принадлежит. Но это невозможно, так как пустое множество не содержит элементов по его определению.

Верно и то, что всякое множество является подмножеством самого себя: Л с Л. Попробуйте обосновать это самостоятельно.

Таким образом, каждое множество Л, отличное от пустого множества, имеет по крайней мере два подмножества: 0 и Л. Они называются несобственными подмножествами множества Л. Подмножества множества Л, отличные от 0 и Л, называют собственными подмножествами.

Пустое множество имеет только одно несобственное подмножество — это само пустое множество. Собственных подмножеств множество 0 не имеет.

Число всех подмножеств множества Л обозначают Р (А) и называют степенью множества Л.

Пример 2.3.

Определим степень множества К = {2, 3,5}. Для этого составим все подмножества данного множества: {2, 3>, {2,5}, {3, 5}, {2}, {3}, {5} — собственные подмножества. Еще есть два несобственных подмножества. Таким образом, у данного множества всего 8 подмножеств и Р (К) = 8.

Заметим, что обычно в одном рассуждении рассматриваются множества, которые являются подмножествами некоторого множества. Это множество для данного рассуждения называется универсальным множеством. Его обозначают буквой U (иногда Е). Например, при рассмотрении различных числовых множеств универсальным множеством является множество действительных чисел; при рассмотрении множеств точек плоскости (различных плоских геометрических фигур) универсальным множеством является множество всех точек плоскости.

Вторым отношением между множествами является отношение равенства.

Определение 2.2. Говорят, что множества, А и В равны, и пишут Л = В, если одновременно имеет место Л с В и В с Л, т. е. каждый элемент множества Л является элементом множества В и каждый элемент множества В является элементом множества Л.

Другими словами, два множества равны, если их элементы совпадают. Так совпадают все элементы множеств натуральных чисел и положительных целых чисел; множества букв слов «множества» и «жеманство» равны, т. е. {м, н, о, ж, е, с, т, в, а} = {ж, е, м, а, н, с, т, в, о}.

Из примера ясно, что для множества важно, какие элементы в него входят, а вот порядок элементов не имеет значения. Еще важно, что в множестве не записывают один и тот же элемент несколько раз.

Чтобы доказать равенство двух множеств, нужно взять произвольный элемент из первого множества и показать, что он принадлежит второму множеству и, наоборот, взять любой элемент из второго множества и показать, что он принадлежит первому множеству.