Гибкость мышления. 
Психология детской одаренности

Способность быстро и легко находить новые стратегии решения, устанавливать ассоциативные связи и переходить в мышлении и поведении от явлений одного класса к другим, часто далеким по содержанию, называют гибкостью мышления. Существует и противоположное свойство — инертность или ригидность мышления. Много внимания данному вопросу уделено в исследованиях К. Дункера, А. М. Матюшкина, Л. Секея и др. Высокий уровень гибкости мышления — явление редкое, как и крайнее выражение его противоположности — инертности мышления. Поэтому наличие первого свидетельствует об исключительности, характерной для одаренных.

Гибкость мышления тесно связана с богатством и разнообразием прошлого опыта человека (объем знаний, умений, навыков и т. п.), однако полностью им не определяется (К. Дункер, Л. Секей и др.). Экспериментальные исследования свидетельствуют о том, что связь между ними имеет очень сложный характер. Так, в некоторых ситуациях объем знаний не только не содействует генерированию новых идей и стратегий, но, напротив, выступает как сдерживающий фактор. Само по себе количество информации еще не является гарантией способности к ее комбинированию и созданию на этой основе новых идей и стратегий. В ходе специальных исследований было определено, что решающим фактором, содействующим развитию этой интеллектуальной характеристики, выступает не опыт, а метод его усвоения. Отсюда и важный педагогический вывод: имеет значение не столько то, чему мы учим, сколько то, как мы это делаем.

В работе по развитию мышления детей мы постоянно использовали задачи на сериацию. Это очень популярные еще со времен Ж. Пиаже задачи, их обязательно включают в курсы по развитию логического мышления детей. Сериация лежит в основе представлений о порядковом числительном, в основе использования различных шкал и измерительных инструментов. Решающий должен выявить закономерность в расположении фигур и продолжить ряд. Например, надо нарисовать фигуру вместо точек:

Один мальчик продемонстрировал то, что называется гибкостью мышления. Он предложил вместо точек поставить первую фигуру, тогда вторая может быть расположена после нее, затем третья… «Как в орнаменте», — сказал он. Такое решение не входило в план урока, однако нельзя было не согласиться, что этот вариант может быть признан как правильный. После этого возникло еще несколько способов, например, поставить вместо точек третью фигуру, затем вторую и, наконец, первую. Повторяя фигуры, наклонять их под разными углами и т. п.

Однажды во время перемены педагог нарисовал на доске задачу на сериацию, изображенную ниже.

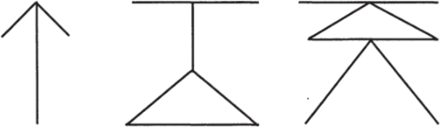
Первоклассники не видели, как это было сделано. Когда стали ее решать, возникли трудности. Дети пытались найти закономерности, логику расположения элементов, составляющих фигуры, в движении линий, но никаких закономерностей в этом не было. Решение не получалось, а увидеть в изображенных фигурах зеркально расположенные цифры почтового индекса не удавалось. Многие дети были чрезвычайно расстроены, большинство из них решали аналогичные задачи легко—и вдруг неудача!