Квантование как проблема собственных значений. 
Операторы физических величин

Уравнение Шредингера в форме (2.16) показывает, что в результате воздействия оператора Гамильтона (2.14) на волновую функцию получается та же волновая функция, помноженная на постоянное значение энергии. При таком условии говорят, что поставлена задача на собственные значения оператора, в данном случае оператора Гамильтона. При соблюдении указанных физических требований на волновую функцию и при соответствующих граничных условиях решение этой задачи существует не при любых значениях постоянной ?, а лишь при строго определенных, образующих энергетический спектр рассматриваемой системы: E_VE_V…. Эти значения называют собственными значениями энергии, а соответствующие им волновые функции ф, ф₂,… — собственными функциями.

Квадрат модуля собственной волновой функции ф_л определяет плотность вероятности того, что квантовая система находится в элементе объема dV вблизи точки г в состоянии со значением энергии Е_п. По формуле полной вероятности:

Рассмотрим теперь уравнение Шредингера (2.16) для собственной функции ф_т с собственным значением энергии Е_т и для собственной функции ф^с собственным значением Е_п. По физическому смыслу собственные значения энергии должны быть действительными величинами. Будем считать, что эти значения энергии различны:

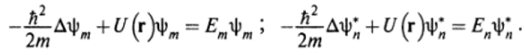
Умножим первое из этих уравнений на ф', а второе — на ф_т и затем вычтем одно из другого: (Е_т — Е_п)ф_тф; = «2~^div (^У^т ~)• Интегрируя по всему пространству с использованием теоремы Гаусса—Остроградского, получаем: (Е_т — E_n)fff = 0 • Так как, по условию, Е_т* ?_я, то отсюда следует соотношение: = 0. Оно показывает, что собственные волновые функции, отвечающие разным собственным значениям, взаимно ортогональны.

Вместе с формулой (2.23) полученное соотношение может быть записано единым образом как условие ортонормировки собственных волновых функций:

где — символ Кронекера, ^П

и, л т.

Существование дискретных состояний атомов было доказано в первых опытах Франка и Герца, и энергетический спектр, т. е. совокупность собственных значений энергии, измеряют теперь различными методами с очень высокой точностью.

В квантовой механике принимается, что измеряемые на опыте значения физических величин, так же как значения энергии, являются соответствующими собственными значениями. Для их определения необходимо данной физической величине сопоставить соответствующий оператор (Борн, 1926). Таким образом, если F — некоторая физическая величина, то ей сопоставляется оператор F, для которого аналогично (2.16) ставится задача на собственные значения, которые образуют спектр величины F. В общем спектр может быть дискретным, составленным из дискретных значений /], F₂,…, и.

непрерывным, простирающимся по всей области задания величины F. Для удовлетворения принципу суперпозиции квантовые операторы должны быть линейными. Такие операторы определяются условиями: F (^_{ +t|>₂)=/tyi +/ty₂* /*(яф)= tf/ty, где ф, ф₂ — произвольные функции; а — произвольная постоянная.

В случае дискретного спектра задача на собственные значения ставится аналогично (2.16):

Собственные функции удовлетворяют условию ортонормировки (2.24). Если квантовая система описывается произвольной волновой функцией Ф, то в результате измерения величины /* должно получиться одно из собственных значений F_n, которому соответствует собственная функция ф_/;. Отсюда следует, согласно принципу суперпозиции, что волновая функция Ф, в общем, должна быть представлена в виде линейной комбинации собственных функций ф_я оператора F:

где а_п — некоторые коэффициенты.

Используем условия нормировки волновой функции и ортонормировки собственных функций (2.24). В результате получаем.

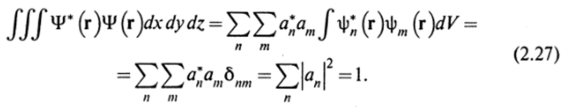
Отсюда следует, что величину |д_я|² можно интерпретировать как вероятность того, что величина /'имеет значение F_n. Умножая (2.26) на ф^ и используя условие (2.24), находим, что коэффициенты разложения (2.26) определяются формулой.

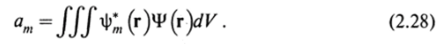
Среднее значение величины /'определяют по общим правилам теории вероятностей как сумму собственных значений, умноженных на соответствующую им вероятность:

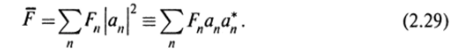
Преобразуем это выражение, используя соотношения (2.28), (2.25), (2.26):

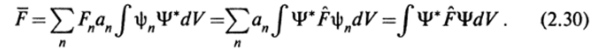
Отсюда следует, что среднее значение любой физической величины можно вычислить в координатном представлении волновой функции, если известен соответствующий оператор в этом представлении. Напоимер, среднее значение импульса равно: р = J Ф* (г)(-/ЛУФ (г)У^. Когда система находится в состоянии, описываемом собственной волновой функцией, то среднее значение величины /'сорпадает с собственным значением:

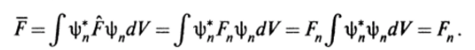
В этом случае коэффициент а_п = 1 (при фиксированном я), а остальные коэффициенты обращаются в нуль.

Собственные значения физических величин, а также их средние значения являются действительными величинами. Этот факт накладывает ограничения на свойства квантово-механических операторов. В самом деле вещественность среднего значения оператора означает, что должно выполняться интегральное соотношение:

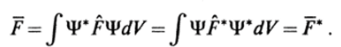
В этом случае говорят, что оператор F — эрмитов оператор. Более общее условие эрмитовости оператора определяется соотношением:

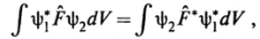
где ф, ф₂ — произвольные функции.

Таким образом, операторы физических величин в квантовой механике должны быть линейными и эрмитовыми. Нетрудно показать, что, например, оператор импульса и оператор Гамильтона удовлетворяют этим условиям.

В стационарных состояниях собственные волновые функции являются функциями вида: ф_л (г,/)=ф_Л (г)е~^/?я//*. В этом случае состояние, описываемое функцией с разложением (2.26), не является стационарным. Подставляя такую функцию в (2.30), получаем.

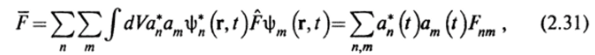
где а_п — коэффициенты, а_п (/)= а_ле^_'^?" ^,'^Л.

Величина.

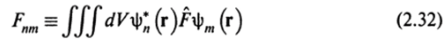
называется матричным элементом оператора F, соответствующим переходу из состояния п в состояние т.

Временная зависимость в (2.31) определяется множителем ^ехр ('4,т0> ^{где ш}гт — частота перехода, ш_пт = (?" - Е_т)/h. Совокупность всех матричных элементов образует матрицу оператора F. Диагональные элементы этой матрицы.

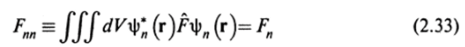
являются средними значениями величины F в состоянии с волновой функцией Пусть, например, F = ex — дипольный электрический момент. Тогда из формулы (2.33) следует, что диагональные элементы матрицы дипольного момента равны нулю, потому что интеграл в симметричных пределах от нечетной функции обращается в нуль (когда состояние не вырождено). Если величина F — энергия, то среднее значение энергии равно Е — ^а* (t)a_m {t}H_nm, где Н_пт — Mart,/!".

тричный элемент оператора Гамильтона. Так как матрица оператора Гамильтона диагональная, т. е. = /Г 6 _т, то? = a* (t)a_m (t)E .

Отсюда видно, что величина д* (t^ (/)= |а_п (/)|² представляет собой вероятность того, что при измерении энергии в момент времени 1 получим значение Е_п. Поскольку |^_п(/)| =|д_я(0)|, то приходим к выводу, что вероятность значения энергии Е_п в любой момент времени не зависит от времени. Это означает, что рассматриваемые состояния стационарны.

Если F — физическая величина с непрерывным спектром, то задача на собственные значения формулируется аналогично (2.25):

где — собственная функция, соответствующая собственному значению F.

Аналогично (2.26) можно рассматривать волновую функцию произвольного состояния в виде суперпозиции собственных функций:

Здесь интегрирование ведется по всей области значений величины F. По аналогии с дискретным спектром можно считать, что выражение |я_/,|²*//^г представляет собой вероятность того, что величина F в состоянии с волновой функцией ty_F имеет значения в интервале /*, F+dF. По смыслу вероятностей.

Аналогично (2.27) можно записать: J ФФ*dV = J |^_F|²1//⁷. Учитывая разложение (2.35), получаем: J dV J dF^a^y. = J dFa^m_Fa_F.

Сравнивая эти два выражения, находим формулу, определяющую коэффициенты разложения (2.35), которая аналогична (2.28):

Рассмотрим условие ортонормировки собственных функций |>_р Для этого подставим разложение (2.35) в формулу (2.37):

a_F = Ja_F, (JdVJy (r'jjdF'. Поскольку это соотношение долж, но быть тождеством при произвольных a_F, то необходимо выполне;

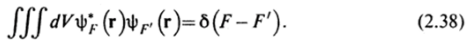
ние условия:

Это и есть искомое условие ортонормировки собственных функций операторов с непрерывным спектром.

Здесь — дельта-функция, введенная Дираком. Она об ладает свойствами: 6^)=0 при q⁰‘, б (Ь)=оо;

— ОС.

Jf (q)b (q — q_Q) dq = f (q₀)> где /(?) ~~ произвольная функция, непрерывная при q = q₀- В дальнейшем будет использовано представление 6-функции эо в виде: 6(<7)=-^- J t^iqxdx.

— 00.

Отметим еще одно соотношение, возникающее при подстановке (2.37) в (2.35): Ф (г)= J^(^r)(f dFp_F (г')ф^ ®)dr'. Отсюда следует, что должно выполняться условие: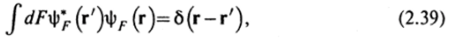

где б (г-г') — трехмерная 6-функция, б (г-г^,)=б (х-х^,)б (₁у-У)х хб (z-z').

Аналогичное соотношение есть и в случае дискретного спектра:

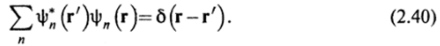
Соотношения (2.35) и (2.37) совершенно симметричны. В этой связи используют следующую терминологию: волновая функция ф (г), как уже сказано, называется волновой функцией в координатном, или г-представлении, а совокупность амплитуд a_F называют волновой функцией в F-представлении.

Примерами величины Fс непрерывным спектром могут служить координата и импульс частицы. Если F, например, координата х, или функция координат F (x, y, z), то по смыслу волновой функции и согласно определениям (1.89) и (2.30) оператором координаты (или функции координат) является просто операция умножения на эту координату (или функцию координат). Если величина F — импульс, то для нахождения среднего значения импульса, а также дисперсии необходимо учитывать определение оператора импульса.

(2.15). Если F— функция координат и импульса вида /'(г, р), то этой функции в координатном представлении сопоставляется оператор F = F (г, р). В импульсном, или^{-представлении,} оператор импульса сводится просто к умножению на этот импульс, а координате отвечает соответствующий оператор: г = /Л —. Такое выражение можно по;

ар лучить, используя выписанные ранее определения средних величин.

Определим собственные функции и собственные значения оператора импульса (2.15). Согласно общим правилам,.

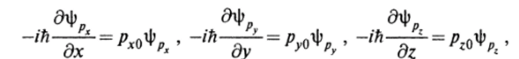
где p_x0, p_y0, p_z0 — некоторые заданные значения компонент вектора импульса.

Решение первого уравнения: (х)= Лехр (/р_х0х//*). Это реше;

ние конечно при всех значенияххпри любом вещественном значении величины р_х0 . Таким образом, собственные значения компоненты импульса р_х образуют непрерывный спектр со значениямиоо… + оо.

Эти значения вместо р_х0 будем обозначать как р_х. То же самое относится, конечно, и к другим компонентам вектора импульса. Поскольку они независимы, то волновая функция, описывающая состояния с определенными значениями всех трех компонент вектора импульса, равна произведению найденных решений: ф_р (г)= Лехр (/'рг/й). Волновая функция, отвечающая состояниям с непрерывным спектром, удовлетворяет условию нормировки (2.38), поэтому.

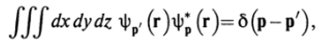
где б (р) — трехмерная 6-функция, б (р)=Ь (Р_х)Ъ (р_у')Ь (р₁) — Используя определение 6-функции, получаем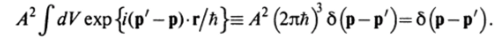

Здесь учтено свойство 6-функции: б (#/й)= йб (А = (2лй) ^².

Рассмотрим теперь формулу (1.92). С учетом сказанного видно, что разложение волновой функции в интеграл Фурье есть не что иное, как ее разложение по собственным функциям оператора импульса.

В качестве примера рассмотрим задачу об эволюции волнового пакета. Допустим, что в начальный момент времени / = 0 задан волновой пакет в форме ф (г, 0)= А ехр-?-г²/4а² -±/(р₀г)/л j-. Плотность вероятностей имеет гауссов вид: |ф (г, 0)|² = А² ехр (-г²/2я²) с центром в начале координат. Вектор плотности потока вероятности (2.21) описывается формулой j (r, 0)= (р₀/т)|ф (г, 0)|. В этих.

^-г²/2я²^=1. Здесь тройной ин;

формулах г² = х² 4-у² + z²; величина а характеризует ширину волнового пакета и определяет среднеквадратичное отклонение по координатным осям, например, bx^Jx² = а вектор р₀ — начальный импульс частицы; А — постоянная нормировки, определяемая из условия (1.87): A² JJJdxdydzexp теграл сводится к произведению трех интегралов Пуассона вида:

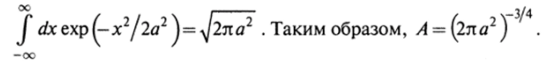
Как теперь определить форму волнового пакета в момент времени /? Для этого представим функцию ф (г, 0) в виде разложения Фурье: ф (г, °)= JJJ <�фф (р, 0) ехр (;рг/й), где Ф (р, 0) — фурье-амплитуда начальной волновой функции, которая определяется обратным преобразованием Фурье: Ф (р, 0)=(2яй) ³ fff ^^гФ (г, 0) ехр (—/р-г/й). Поскольку начальная волновая функция задана, величину Ф (р, 0) можно вычислить, при этом вычисления опять сводятся к интегралам Пуассона, так что фурье-амплитуда в начальный момент времени также имеет гауссову форму: Ф (р, 0)= (2яр²) ехр (-|р-р₀|²/4/?²). Это волно вая функция в импульсном представлении в начальный момент времени. Среднее значение импульса р равно р₀, а величина р_] = h/2a определяет среднеквадратичное отклонение в каждом направлении, например, Ар_х = — р_0х)² = р_]. Таким образом, в начальный мо мент произведение АхАр_х = Ь/2 в соответствии с соотношением неопределенностей. В момент времени t волновую функцию также можно разложить в интеграл Фурье: ф (г,/)= JJJ^рф (р,/)ехр (/р г/й). Волновая функция ф (г, /) удовлетворяет уравнению Шредингера (2.13) (при U = 0), из которого следует уравнение для волновой функ;

вФ (р,/) р² / ч ции в импульсном представлении: ih——- = — Ф (р,/). Отсю;

dt 2т ⁴ '

да: Ф (р,/)=Ф (р, 0) ехр (-/р²//2тЛ V Обратим внимание, что в этой формуле р²/2т=Е_к, где Е_к — энергия частицы, что характерно для стационарных состояний. Это связано с тем, что для свободной частицы собственные состояния импульса стационарны. Таким образом, ф (г,/)= ²//2тУ Функция Ф (р, 0).

известна, тогда после вычислений, аналогичных предыдущим, получаем.

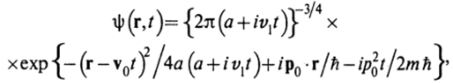
где v, =р Jm, v_Q = р₀/т. Такой волновой функции отвечает плотность вероятности.

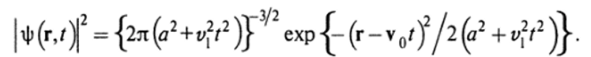
Это — расплывающийся волновой пакет, бегущий с групповой скоростью v_Q с уменьшающейся амплитудой и возрастающей шириной Дх (/)=^а² +t;,² /². Аналогичными формулами определяют отклонения Ду (/) и Дг (/). Зная функцию Ф (р, /), можно вычислить средние значения величин, зависящих от импульса, в частности, отклонения Др_х(/), с учетом формулы.

/)| dp_xdp_ydp_z. Вычисления приводят к интегралам Пуассона. Можно найти также вектор плотности потока вероятности: j (г, /)= |ф (г,/)| -jv₀ +1/² / (гv_Q / ypw-O}.

В случае тел с большой массой (макроскопических тел) расплывание пакета пренебрежимо мало, и поток остается пропорциональным скорости v_Q.

ЗАДАЧИ.

1. Показать, что оператор импульса — эрмитов оператор.

Решение. С использованием естественного граничного условия получаем.

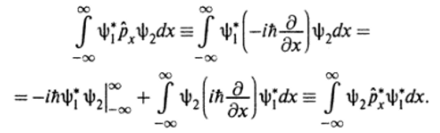
2. Показать, что оператор импульса связан с оператором бесконечно малого смещения (однородность пространства).

Решение. При смещении начала координат вдоль оси х на величину бх новые координаты связаны со старыми соотношениями: х' — х-Ьх, У = у, Z* — Z ? Тогда.

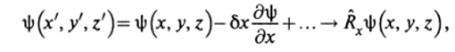
где /Г — оператор смещения (сдвига), R_v = 1 — —6xp_v.

X X ft X

3. Найти собственные функции оператора координаты в координатном представлении.

Решение. По общим правилам х (х)= jc₀t|j^ (х), где д:₀ — конкретное значение координаты х. Поскольку оператор координаты сводится просто к умножению на координату, то при собственная функция ф^(х)=0. Из условия ортонормировки (2.38) следует:

J*dx (х)ф_х/ (х)=б (х₀ -^о) — Отсюда, используя свойства 6-функции, получаем: (х)=б (х-х₀). Аналогично определяются собственные функ ции по другим координатным осям, так что, в общем, волновая функция в координатном представлении с заданными координатами имеет вид: ф_Г) (г)= б (г — г₀). Совершенно аналогично определяются собственные функции оператора импульса в импульсном представлении: ^_Р(р)=б (р-р₀).

4. Найти собственное значение оператора F = —*Ц- + х², если его собственная функция = exp (~x²/2j.

Решение. Используя определение (2.34), получаем F= 1.

5. Найти собственные функции и собственные значения оператора.

F =—d-т при граничных условиях 1|)(о)=ф (о)=0.

dx² / / ^

Решение. Уравнение осциллятора с «частотой» у[7: = Fy>, при этом ф (х)= As {xy[F)+ Bcos (x>[f). С учетом граничных условий постоянная В = 0, собственное значение /^г = (шх/а), гдея = ±1,±2, …

6. Убедиться, что = J dp |ср (р, /)| =1.