Составление плана экспериментов

В полном факторном эксперименте (ПФЭ) реализуются все возможные сочетания уровней факторов. Общее число опытов равно n=2^k, где k — число факторов. В рассматриваемом случае k=2, n=2²=4.

В табл. 1 приведены условия эксперимента в виде матрицы планирования, где строки соответствуют различным опытам, а столбцы — кодированным значениям факторов.

Таблица 1. Таблица планирования для двух факторов 2².

Примечание: номера опытов соответствуют номерам точек факторного пространства (рис. 1).

Проведение эксперимента и обработка результатов

При проведении экспериментов реализуются фактические значения факторов, соответствующие кодированным значениям. В табл. 2 приведены результаты численного эксперимента, выполненного в соответствии с принятым планом. Каждый опыт производился один раз (без проведения параллельных опытов). В графе приведены полученные значения функции отклика. регрессия экстремум градиент функция Для определения дисперсии Y и величины ошибки (среднеквадратического отклонения) проведем серию численных опытов при значениях факторов, соответствующих нулевому уровню (координатам центральной точки, указанной ранее).

Ориентируясь на условия проведения реальных экспериментов, связанных с значительными затратами времени и средств, ограничимся проведением трех численных опытов с помощью программы «Моделирование процессов вероятностного характера», результаты которых приведены ниже:

Таблица 2. Результаты численного эксперимента.

По результатам эксперимента находим значения коэффициентов по формуле:

В частности, для модели.

и двух факторов.

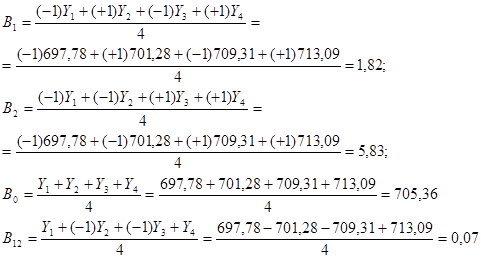
Значение коэффициента для каждого фактора соответствует вкладу данного фактора в параметр оптимизации при переходе фактора с нулевого уровня на верхний или нижний. Вклад, определенный при переходе от нижнего уровня к верхнему, называется эффектом фактора (иногда его называют основным или главным эффектом). Он численно равен удвоенному коэффициенту.

В рассматриваемом случае Коэффициент взаимодействия B₁₂ практически равен нулю, поэтому его действие может не учитываться. Производим проверку воспроизводимости численных экспериментов (однородности дисперсий, полученных при проведении параллельных опытов по критерию Кохрена.

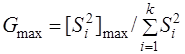
=204,828/735,329=0,279.

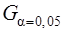
По таблице приложения 1 находим табличное (критическое) значение критерия при уровне значимости б=0,05 и k=N=4 =0,6287. Расчетное значение критерия существенно меньше критического, следовательно, рассматриваемые дисперсии однородны и численные эксперименты отвечают требованиям воспроизводимости. Дисперсия значений функции отклика при одинаковом количестве параллельных опытов равна среднему значению.

.

Проводим анализ адекватности выбранной модели (вида полинома) опытным данным по критерию Фишера F. Оценки дисперсий в формуле расчета критерия расставляются так, чтобы его величина была больше единицы Оценку дисперсии адекватности в случае отсутствия дублирования опытов производим по формуле:

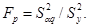
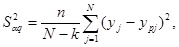
где — расчетное значение Y, вычисленное по полученному уравнению регрессии при подстановке в него опытных данных значений Х_j; k — количество коэффициентов в уравнении регрессии; - число степеней свободы; n — количество параллельных опытов.

В рассматриваемом случае. Расчет приведен в табл.3.

Таблица 3. Расчет.

№ опыта.	Х1	Х2	Х12
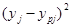	— 1.	— 1.	— 1.	613,12.	613,12.	0,00.
	+1.	— 1.	+1.	777,34.	777,34.	0,00.
	— 1.	+1.	+1.	756,27.	756,27.	0,00.
	+1.	+1.	— 1.	672,78.	672,78.	0,00.
Сумма.	;	;	;	;	;	0,00.

Так как, то.

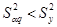
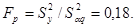
Табличное значение F_Т при (для), (для) и уровне значимости 0,05 равно 241. То есть, что свидетельствует о том, что принятая модель адекватна. Об этом свидетельствует и сопоставление результатов расчета по полученному полиному и результатов эксперимента (табл.1) — разница результатов равна нулю.

Проверяем статистическую значимость коэффициентов полинома. Доверительный интервал для jтого коэффициента определяется по формуле.

Здесь t=2,262 — квантиль распределения Стьюдента при числе степеней свободы, с которыми определялась дисперсия для вероятности 0,95, равной выбранному уровню значимости 0,05. Доверительные интервалы.

Как следует из полученных выражений, все коэффициенты не равны нулю и являются, следовательно, статистически значимыми.

При оценке адекватности модели возможны следующие случаи:

1. Линейная модель адекватна. При этом ни один из эффектов взаимодействия не может быть значим. Принятие решения определяются значимостью линейных коэффициентов.

Если все линейные коэффициенты незначимы, то в первой серии опытов были выбраны слишком узкие интервалы варьирования факторов. Следующим шагом должно быть повторение эксперимента при более широких интервалах. Может оказаться, что почему-либо нельзя расширять интервалы. Тогда можно рекомендовать многократное повторение той же самой серии опытов, в результате которых при статистическом усреднении обычно удается выделить значимые коэффициенты.

Если все коэффициенты значимы, то решение однозначно — переходят к движению по градиенту. Может оказаться, что один из коэффициентов резко несимметричен. Тогда движение по его градиенту выродится в обычный однофакторный эксперимент, который менее эффективен. Поэтому в этих случаях следует повторить эксперимент, уменьшив интервал варьирования этого фактора или увеличив интервалы других факторов.

Наиболее часто встречается случай, когда часть линейных коэффициентов значима, а часть незначима. Здесь важно определить судьбу незначимых факторов. Если первой серии предшествовало экспериментальное отсеивание факторов и незначимым оказался слабый эффект, включенный в планирование эксперимента по осторожности то, получив для него незначимый коэффициент, можно его отсеять. Если же отсеивание не предшествовало первой серии, то отбрасывать фактор только по незначимости коэффициента рискованно. Обычно расширяют его интервал варьирования в следующей серии, и только если и там он окажется незначимым, то его отсеивают. Отсеивание приводит к уменьшению числа факторов и позволяет значительно упростить задачу.

2. Линейная модель неадекватна. В этом случае значим хотя бы один коэффициент взаимодействия. Возможны несколько причин неадекватности.

Чаще всего неадекватность возникает в результате неудачного выбора интервалов варьирования. В этом случае центр плана (нулевая точка) переносится в экспериментальную точку, давшую наилучшие или одно из наилучших значение параметра оптимизации, а интервалы варьирования уменьшаются тем сильнее, чем больше по абсолютной величине коэффициенты уравнения регрессии.

Другой причиной неадекватности, кроме выбора интервалов варьирования, является попадание нулевой точки в «почти стационарную область», близкую к оптимальной точке. На первых этапах планирования это получается редко. Если известно предельное значение параметра оптимизации, то о близости к оптимуму можно судить по его значениям в опытах. Если предельное значение неизвестно, то критерием служит движение по градиенту. Когда оптимальная область действительно достигнута, то в зависимости от постановки задачи либо исследование заканчивается, либо изучают «почти стационарную» область.

Решение о движении по градиенту можно принимать и при неадекватной модели. Вне оптимальной области модель не нужна — нужен трамплин для быстрого попадания в эту область. При движении по градиенту ставят весьма мало опытов. Если движение по градиенту окажется удачным, то новый план будет ставится в уже более благоприятной области. Если же исследователь потерпит неудачу, то он вернется назад и изменит интервалы варьирования. Потери при этом обычно невелики.

Может оказаться, что после включения нескольких эффектов взаимодействия модель станет адекватной. Конечно при сохранении числа степеней свободы. Тогда возникает задача движения по градиенту нелинейной модели. Эта задача имеет решение, но ее сложность препятствует ее практическому использованию. Обычная альтернатива — движение по градиенту неадекватной модели.

В рассматриваемом случае решение одно — переходить к движению по градиенту.