Быстрое преобразование Фурье

Соотношение (6.19) показывает, что для определения одного коэффициента ДПФ сигнальной последовательности из N отсчетов необходимо выполнить около N операций умножения на комплексное число и столько же сложений, а для нахождения всех коэффициентов — N² вычислений. В частности, при N = 2¹⁰ = 1024 надо осуществить чуть более миллиона (1024²) умножений и сложений. Если длины обрабатываемых массивов превышают тысячу, то дискретная обработка в реальном масштабе времени требует увеличения мощности и усложнения вычислительных комплексов. Однако разработан способ выполнить преобразования значительно быстрее. Способ называют быстрым преобразованием Фурье (БПФ).

Нетрудно заметить, что среди множителей ДПФ есть много повторяющихся значений. Алгоритм БПФ группирует слагаемые с одинаковыми множителями, значительно сокращая число умножений. В результате быстродействие БПФ может в зависимости от N в сотни раз превосходить быстродействие стандартного алгоритма ДПФ (кстати, число N называется размером или длиной БПФ).

В основу алгоритма БПФ положен принцип разбиения (прореживания во времени) заданной последовательности отсчетов исходного дискретного сигнала на ряд промежуточных последовательностей (подпоследовательностей) и децимации (выбрасывание отсчетов, порядковый номер которых кратен определенному числу). Это значит, что число отсчетов дискретного сигнала N разделяют на множители (например, N = 8 = 2 • 2 • 2, N = 60 = = 3−4 -5). Затем определяют спектры этих промежуточных последовательностей и через них находят спектр всего сигнала. В зависимости от состава, числа и порядка следования множеств создают различные алгоритмы БПФ. В цифровой технике удобнее обрабатывать сигнальные последовательности со значениями числа отсчетов АГ, являющимися степенью с основанием 2 (4,8,16 и т. д.). Это позволяет многократно делить входную последовательность отсчетов на более мелкие подпоследовательности.

Пусть требуется вычислить ДПФ последовательности (массива отчетов) дискретного сигнала {u (kAt)} = {и_к}, имеющей четное число отсчетов (рис. 6.12, а), причем N= 2', где г — целое число (если условие не выполняется, то последовательность искусственно дополняют нулями до требуемого значения N). Представим входную последовательность в виде двух подпоследовательностей с четными и нечетными номерами и половинным числом членов в каждой (рис. 6.12, б, в):

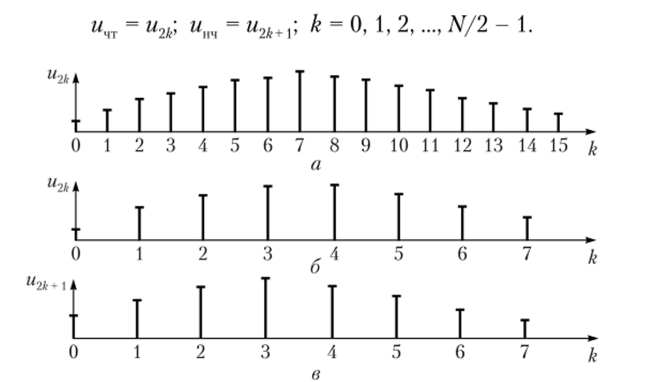
Рис. 6.12. Последовательности и подпоследовательности дискретного сигнала:

а — входная; 6 — с четными номерами; в — с нечетными номерами Коэффициенты ДПФ для подпоследовательностей с четными и нечетными номерами запишем отдельно:

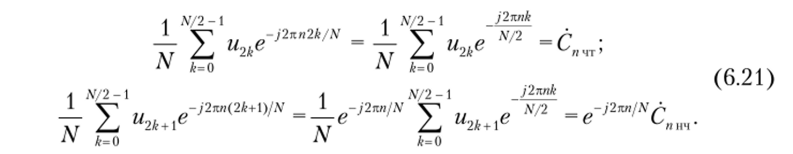
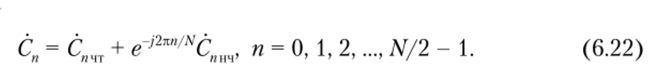
Коэффициенты С_п результирующего ДПФ входной последовательности выразим через параметры С_;/чт и С_пнч двух вновь введенных подпоследовательностей. Из равенств (6.21) нетрудно заметить, что в диапазоне номеров отсчетов от 0 до N/2 — 1 ДПФ входной последовательности определяется соотношением Так как ДПФ четной и нечетной подпоследовательностей являются периодическими, имеющими период следования N/2, то.

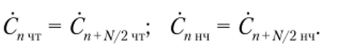
Входящий в формулу (6.22) экспоненциальный множитель при п > N/2 будет равен.

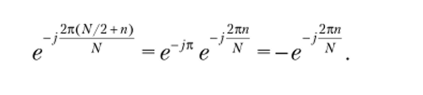
С учетом двух последних выражений находим ДПФ входной последовательности для отсчетов с номерами от N/2 до N — 1:

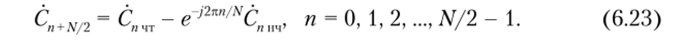
Соотношения (6.22) и (6.23) представляют собой фундаментальные алгоритмы БПФ. Экспоненциальные фазовые множители e~^j2nn/N в алгоритмах учитывают влияние сдвига нечетной подпоследовательности относительно четной.

Чтобы еще уменьшить число вычислений, четную и нечетную подпоследовательности разбивают каждую на две промежуточные части. Разбиение продолжают вплоть до получения простейших двухэлементных последовательностей. Определив ДПФ простейших пар отсчетов, можно вычислить ДПФ четырехэлементных, восьмиэлементных и т. д. подпоследовательностей. При объединении ДПФ четной и нечетной подпоследовательностей используют алгоритмы (6.22) и (6.23), подставляя в них соответствующие значения коэффициентов N и п.

Нетрудно заметить, что вычисление по формулам (6.21) не требует операций умножения, а только сложения и вычитания комплексных чисел. Учитываться же должны лишь операции умножения в алгоритмах (6.22) и (6.23) для различных п при разбиениях массива отчетов на мелкие подпоследовательности. Число этих операций при первом разбиении составляло N/2. Такое же число N/2 операций требуется выполнить при каждом следующем разбиении. Таким образом, вдвое увеличивается число подпоследовательностей и вдвое сокращается наибольшее число п в формулах (6.22), (6.23).

Вычисление коэффициентов ДПФ последовательности из N отсчетов, но алгоритмам БПФ требует совершения примерно iVlog₂Nопераций умножения. Алгоритмы БПФ сокращают число операций по сравнению с алгоритмами ДПФ в N²/(Nog., N) = iV/log._;iV раз. В частности, при числе отсчетов обрабатываемого сигнала N= 2¹⁰ имеем log₂N = 10, и сокращение числа операций будет JV/log₂JV ~ 100. При очень больших массивах отсчетов входного сигнала выигрыш в скорости обработки может достигать нескольких тысяч. При этом следует подчеркнуть, что алгоритм БПФ является очень точным. Он даже точнее стандартного ДПФ, так как, сокращая число операций, он приводит к меньшим ошибкам округления.

Таким образом, в основу алгоритмов БПФ заложены операции сложения и вычитания с умножением одного из компонентов на экспоненциальный множитель e~^J2nn ‘^w. Это базовая операция алгоритма БПФ с прореживанием по времени, получившая в отечественной цифровой технике жаргонное название «бабочка», поскольку диаграмма похожа на стилизованное изображение этого насекомого, а также по ассоциации с изображением ее направленного графа. Кружок на линиях графа обозначает арифметическую операцию сложения/вычитания, верхний выход соответствует сумме, нижний — разности, стрелка обозначает операцию умножения на поворачивающий множитель, стоящий над этой стрелкой.

Особенность построения сигнального графа, но алгоритмам БПФ рассмотрим на примере вычисления коэффициентов С_п для восьмиэлементной (N = 8) последовательности сигнала (рис. 6.13). Узлы (вершины) графа со;

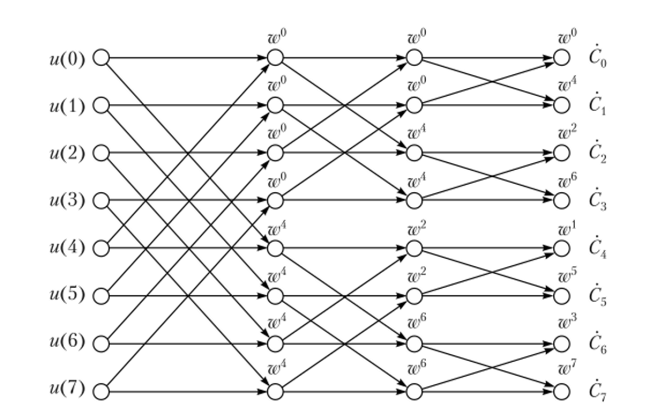
Рис. 6.13. Сигнальный граф БПФ для N = 8 отсчетов входного сигнала.

ответствуют исходным отсчетам и (0),и (1), а также промежуточным и конечным коэффициентам ДПФ. Входящие в любой узел стрелки (дуги графа) обозначают переменные, участвующие в его формировании. Подобное формирование сигнального графа основано на операции суммирования указанных переменных с весовыми экспоненциальными множителями, соответствующими определенному узлу.

Например, сокращенная запись в виде да⁰ означает, что суммирование в узле должно осуществляться с множителем да⁰ = е° = 1, при да¹ — с множителем -1 (да⁴ = е ^/2л4/8 = -1) и т. д. Как очевидно из структуры сигнального графа на рис. 6.13, все коэффициенты ДПФ С₀,…, С₁ восьмиэлементной последовательности вычисляются через две четырехэлсментные, которые, в свою очередь, определяются через четыре двухэлементные ДПФ.