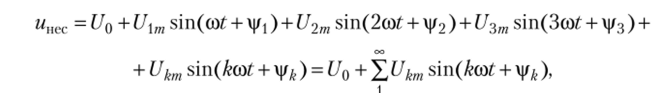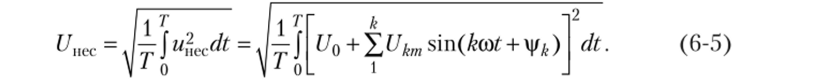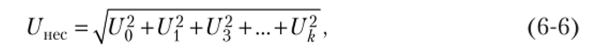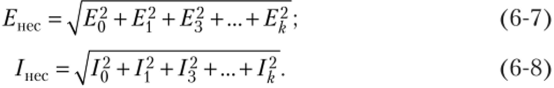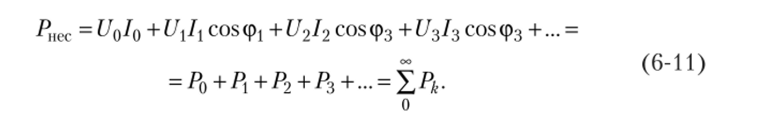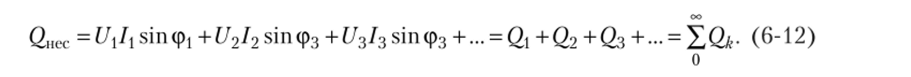Действующие, средние значения и мощность несинусоидальных электрических величин

Действующие значения электрических величин так же, как и синусоидальных, определяются как среднеквадратичные мгновенных значений за период, т. е. по тем же формулам, что и синусоидальные. Например, если несинусоидальное напряжение задано в виде ряда Фурье: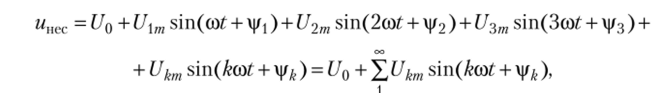

то его действующее значение найдется по известной формуле.

При соответствующих преобразованиях получаем:

т.е. действующее значение напряжения равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений напряжений гармоник и не зависит от их начальных фаз.

По аналогии с (6−6) действующие значения ЭДС и тока будут:

Среднее значение электрических величин найдется как среднее за период:

В отличие от действующего значения среднее зависит от начальной (разы.

3. Под активной мощностью несинусоидального тока понимают среднее значение мгновенной мощности за период первой гармоники, т. е.

Подставив в (6−10) значение и_нес и i_Hec в виде рядов и проделав соответствующие преобразования с учетом того, что средние значения за период произведений синусоидальных функций разных частот равны нулю, получим.

По аналогии с (6.11) реактивная мощность будет.

Таким образом, активная и реактивная мощности несинусоидального тока равны алгебраическим суммам активных и реактивных мощностей отдельных гармоник, если в ряде отсутствует постоянная составляющая. Если же она присутствует, то учитывается только в активной мощности.

Полная мощность в несинусоидальной цени равна.

где [/_нес и /_нес находятся по (6−6) и (6−8).

Поскольку кривые тока и напряжения в общем случае могут отличаться друг от друга, то Для оценки (6.14) вводится понятие мощности искажения

Отношение активной мощности к полной, как и в цепях синусоидального тока, называется коэффициентом мощности

Эквивалентному углу ср_;) можно дать следующий смысл: он есть угол сдвига фаз между эквивалентными синусоидальными напряжением и током, действующие значения которых равны действующим значениям несинусоидальных электрических величин.