Методологическое прерывание 2.11. Судьба аксиомы Архимеда

Не будем прослеживать историю аксиомы Архимеда и обратимся за сведениями о ее судьбе сразу к геометрии нашего времени. Система геометрических аксиом Давида Гильберта, впервые опубликованная в 1899 году и ставшая классической, содержит пять групп аксиом [40]:

I — восемь аксиом соединения (принадлежности);

II — четыре аксиомы порядка;

III — пять аксиом конгруэнтности;

IV — аксиома о параллельных;

V — две аксиомы непрерывности.

Аксиома Архимеда входит в пятую группу вместе с совсем не очевидной аксиомой полноты, утверждающей, что рассматриваемая система точек должна быть такой, чтобы к ней нельзя было бы добавить еще точки, не нарушая других аксиом.

П. К. Рашевский во вступительной статье к изданию [40], содержащему русские переводы работ Д. Гильберта, подчеркивает, что в аксиомах групп I—IVречь идет о конечных конструкциях, но с аксиомами группы V дело обстоит иначе, «и тут лежит пропасть, отделяющая их от предшествующих». И далее: «…безобидная, казалось бы, аксиома Архимеда тоже предполагает понятие о бесконечном множестве». Итогом этих рассуждений Рашевского явился абзац, который он сам выделил курсивом:

Крупнейшим достижением Гшьберта в области логического анализа геометрии явилось как раз то, что он обнаружил возможность развить геометрию во всем существенном, не пользуясь аксиомами непрерывности.

Действительно, Гильберт (как, собственно, и древние греки) построил своего рода исчисление отрезков, не обращаясь ни к понятию числа, ни к аксиоме Архимеда. По терминологии Рашевского это есть неархимедова геометрия в широком смысле.

(аксиома Архимеда в ней не используется). Кроме того, для доказательства независимости аксиом Гильберт весьма искусственным способом построил неархимедову геометрию в узком смысле (аксиома Архимеда в ней не выполняется).

В отечественной метрологии понятие неархимедовой величины до последнего времени не фигурировало. Оно появилось в недавно изданной книге [56] известных метрологов из ВНИИФТРИ, которые положили в основу определения неархимедовых величин «бессмысленность операции сложения этих величин и их интервалов». При таком подходе неархимедовой величиной оказывается, например, твердость материалов.

С нашей точки зрения, это неправильно: аксиома Архимеда предполагает возможность суммирования величин (точнее, объединения характеризуемых ими объектов). Если операция объединения не определена, разговоры о неархимедовости теряют смысл. В подобных случаях величины не следует называть неархимедовыми — они попросту физически неаддитивны.

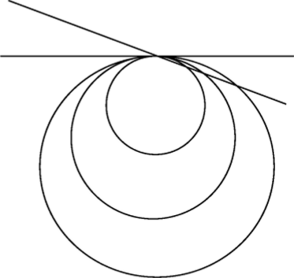
Рис. 2.15. «Роговидные углы» между семейством окружностей и их общей касательной (они всегда лежат внутри угла, образованного касательной и секущей).

Впрочем, похожую неточность допускали сами древние греки, если только И. Г. Башмакова в своих «Лекциях по истории математики в Древней Греции» правильно передала ход их мысли.

Речь идет о «роговидных углах», заключенных между прямой и семейством окружностей, касающихся ее в некоторой точке (рис. 2.15).

На множестве «роговидных углов» операция суммирования не определена, но косвенным образом может быть реализована операция умножения на целое число: один «роговидный угол» больше другого в п раз, если образующая его окружность имеет в п раз меньший диаметр.

При умножении «роговидного угла» в любое число раз его начальная часть (примыкающая к точке касания) всегда будет лежать внутри прямолинейного угла между касательной и какойлибо секущей, проходящей через точку касания.

На этом основании И. Г. Башмакова называет «роговидные углы» актуально бесконечно малыми (с чем можно согласиться) или неархимедовыми величинами [57, с. 311]. Но вот последнее, по нашему мнению, дважды неверно: не только потому, что для «роговидных углов» не определена операция суммирования, но и потому, что семейство «роговидных углов» сравнивается с объектом, не принадлежащим этому семейству, — с прямолинейным углом.

Очевидным примером истинно неархимедовой величины в современной физике может служить скорость движения: относительные скорости легко поддаются физическому суммированию, но, последовательно суммируя какие угодно конечные скорости, нельзя превзойти скорость света.

Возможно, развитие науки приведет к обнаружению других истинно неархимедовых физически аддитивных величин. Например, если бы в окружающем нас мире реализовалась геометрия Лобачевского, то неархимедовой величиной оказалась бы площадь. Об этом знал уже великий К. Ф. Гаусс.

В письме Фаркашу Бойяи (отцу Яноша, независимо от Н. И. Лобачевского открывшего неэвклидову геометрию) Карл Фридрих Гаусс сообщал о своих попытках доказать постулат о параллельных:

«Правда, я достиг многого, что для большинства могло бы сойти за доказательство, но это не доказывает в моих глазах ровно ничего; например, если бы кто-нибудь мог доказать, что возможен такой прямоугольный треугольник, площадь которого больше любой заданной, то я был бы в состоянии строго доказать всю геометрию. Большинство сочтет это за аксиому, я же — нет. Так, могло бы быть, что площадь всегда будет ниже некоторого данного предела, сколь бы удаленными друг от друга в пространстве ни были предположены три вершины треугольника» [4, с. 196].

Сделаем еще два замечания в связи с рассматриваемым вопросом. Согласно аксиоме Архимеда, для любых отрезков a w b

всегда можно найти такое натуральное п, что па станет больше Ь. Эта формулировка легко переводится на язык математической логики: /(a, be Е)3(пе N) a> b, где Е — множество отрезков, N— множество натуральных чисел. И вот первое замечание: существенно, что выявляемое при сравнении отрезков отношение есть отношение порядка, а не эквивалентности.

Порядок во многом удобнее эквивалентности: ведь при реальном сравнении величин строгая эквивалентность не может быть выявлена. Правда, несмотря на это, в конце XIX века Герман Гельмгольц выберет «физическое равенство» в качестве одного из основных понятий своей теории измерений. На равенство величин (опять-таки игнорируя тот факт, что на практике его, строго говоря, невозможно выявить) опирается и современный теоретик А. Д. Александров [46, с. 134].

Получается, что греки мыслили более рационально, чем нынешние физики и математики.

Второе замечание: любая формулировка аксиомы Архимеда исключает понятие отрезка нулевой длины — точки как вырожденного отрезка. Это не особенность аксиомы; напротив, в большинстве современных строгих определений понятия величины нулевые ее значения тоже исключаются.

Например, одна из «аксиом величины» упоминавшегося выше О. Хёльдера [58J звучит так: «Для каждой величины существует меньшая» (как уже было сказано, это положение восходит к Анаксагору). В точности такую же аксиому можно найти у Александрова [46, с. 132]. Но для нулевой величины меньшей нет, значит, она не удоатетворяет аксиомам величины.

В классическом определении величины К. П. Широкова (ГОСТ 16 263—70) содержится условие: «…свойство может быть для одного объекта в определенное число раз больше или меньше, чем для другого», что также исключает нулевое значение «свойства» — нуль не может быть меньше ненулевой величины «в определенное число раз».

Тем не менее, пользуясь приборами, мы привычно «устанавливаем нуль» — например, соединив накоротко входные зажимы вольтметра или не положив ничего на грузоприемную платформу весов. В этих примерах (по-видимому, бывают исключения) объект, характеризуемый нулевым значением величины, — это объект, которого нет. Действительно, напряжением характеризуется объект в виде участка цепи, а короткое замыкание — это не участок цепи. Массой характеризуется некоторая вещь, а «ничего», положенное на чашу весов, не является вещью. Хочется задать вопрос в античном духе: существует ли небытие?

Таким образом, оказывается, что древняя аксиома Архимеда затрагивает помимо всего прочего проблему объектов, характеризуемых нулевыми значениями величин, на которую современные теоретики измерений и философы не обращают внимания.