Возврат из прерывания 3.4

При всей значимости логических работ В. Оккама не следует забывать и о других логиках, работавших в XIV веке. В частности, продолжались исследования логических парадоксов (типа «Лжец»). Много раз упоминавшиеся выше историки логики П. С. Попов и Н. И. Стяжкин пишут о Павле Венецианском (1342−1429):

«Обзор пятнадцати точек зрения на природу парадоксального предложения дает крайний аверроист Павел Венецианский… Например, согласно шестой точке зрения (ее придерживается Марсилий из Ингена) неразрешимое предложение не истинно и не ложное, а есть нечто среднее…» [3, с. 196].

Имя Марсилия Ингенского (1330—1396) нам еще встретится в данном пособии.

Своеобразным мыслителем, продолжившим оккамовские тенденции, был Николай из Отрекура, годы рождения и смерти которого нам неизвестны. Он отделял философию от теологии; считал Бога всемогуществом, недоступным человеческому познанию, а окружающий нас мир — лишенным высшей конечной причины. По Николаю, «в природных вещах нет ничего, кроме пространственного соединения и разъединения атомов» [2, с. 219].

В тексте О. В. Трахтенберга, посвященном Николаю из Отрекура, можно усмотреть некоторое противоречие. С одной стороны, Николай призывает философов обратиться к наблюдению вещей и объяснению природы. Однако, с другой стороны, «Отрекур признает два основных принципа познания: внутренний опыт и принцип противоречия» [2, с. 219]. Но из внутреннего опыта нельзя вывести ничего, относящегося к внешнему миру, а используя принцип противоречия, «невозможно из существования одной вещи вывести существование другой», и поэтому «знание есть только уверенность в своем собственном существовании» [Там же].

Как видим, оккамизм уже в XIV веке (Николай был вынужден отречься перед Парижским университетом от своего учения в 1347 г.) приводил к крайнему субъективизму и скептицизму.

Перейдем теперь ко второму научному направлению, характерному для XIV века, — к учению об интенсии и ремиссии (т. е. об усилении и ослаблении) качеств. Нынешние авторы зачастую смешивают его с учением о широте форм, причем смешивают до такой степени, что иногда говорят об интенсии и ремиссии форм. Некоторую путаницу вносит еще и существование учения о forma fluens и fluxus formae — о текущей форме и течении формы, которое упоминалось выше, в разд. 3.4. Представляется, что эти три учения все-таки различны, хотя и связаны между собой.

Чтобы в этом разобраться, нужно вернуться к Аристотелю и вспомнить его трактовку понятий формы и качества.

В разд. 2.5 была приведена характерная цитата из «Метафизики» Аристотеля:

«…Под материей же я разумею, например, медь; под формой — очертание-образ; под тем, что состоит из обоих, — изваяние как целое. Так что если форма псрвее материи и есть сущее в большей мере, она на том же основании первее и того, что состоит из того и другого».

Таким образом, форма вещи — это то, что делает ее (из некой безличной материи) такой, какова она есть. Понимаемая таким образом форма не может иметь различных степеней, изменения вещи могут обусловливаться только движением ее материи, субстанции.

Но материальным движением средневековые богословы не могли объяснить возможность различий в духовном совершенстве или благодати [30, с. 18]: ведь душа невещественна, и изменение ее свойств не могло быть связано ни с каким перемещением матермального субстрата. Поневоле приходилось признать, что изменяться может сама форма. Таков один из источников учения о широте форм.

Однако термин широта, согласно В. П. Зубову [30, с. 16—17], встречается (в греческом варианте лХатод, которому соответствует более позднее латинское latitudo) уже у Галена, выдающегося врача древности, жившего в 131—200 годы. Будучи врачом, Гален задавался вопросом: может ли здоровье, как некая соразмерность, равновесие элементов, иметь степени?

Казалось бы, равновесие должно быть чем-то единственным. Однако Гален замечает: «Часто случается, что лира кажется настроенной самым лучшим образом, а потом приходит другой музыкант и настраивает ее точнее». Также и здоровье, по Галену, способно растягиваться на довольно большую широту (отметим здесь ссылку на музыкальную практику — думается, что мы сейчас склонны недооценивать роль музыки в развитии науки!). Это рассуждение можно считать другим источником учения о широте форм.

Что касается понятия качества, то оно у Аристотеля, как говорилось в разд. 2.5, неоднозначно. Напомним еще одну цитату, в которой «качество в первичном смысле» немногим отличается от формы.

«…0 качестве можно, пожалуй, говорить в двух смыслах, причем один из них — важнейший, а именно качество в первичном смысле — это видовое отличие сущности… А в другом смысле называются качеством состояния движущегося, поскольку оно движется, и различия в движениях».

В разд. 2.5 были приведены примеры качеств во втором смысле — это «тепло и холод, белизна и чернота, тяжесть и легкость и все тому подобное…». Было сказано и то, что они, по Аристотелю, «допускают большую и меньшую степень. Об одном белом говорят, что оно более бело или менее бело, чем другое». Наконец, там же обсуждалась замечательная цитата из аристотелевской «Физики»:

«Теперь относительно качественного изменения: каким образом одно [изменение] будет иметь равную скорость с другим? Если, например, выздоровление есть качественное изменение, то одному возможно исцелиться скорее, другому медленнее, а некоторым одновременно; следовательно, возможно качественное изменение, проходящее с равной скоростью, поскольку оно произошло в равное время».

В свете сказанного вряд ли можно согласиться с В. П. Гайденко и Г. А. Смирновым, которые, полностью отождествляя форму и качество, утверждают: «…учение о широте форм первоначально возникло в средневековой медицине и фармакологии» как представление «о некоторой области, промежутке, в пределах которого может изменяться качество» (курсив мой. — В. К.) — от здоровья до крайней степени болезни [5, с. 287]. Ведь здоровье как равновесие, о «широте» которого говорил Гален (предположим, что авторы книги [5] имели в виду его), — это совсем не то, что промежуток «от здоровья до крайней степени болезни». И как могло «первоначально возникнуть» в средневековой медицине представление об этом промежутке, если о нем подробно рассуждал уже Аристотель?

Теперь, пожалуй, мы подготовлены к тому, чтобы обсудить связь между тремя средневековыми учениями:

об интенсии и ремиссии качеств;

о широте форм;

о текущей форме и течении формы.

Представляется, что учение об интенсии и ремиссии качеств, если взглянуть на него с современных позиций, имеет два аспекта.

С одной стороны, оно представляет собой попытку какимто образом градуировать тот промежуток возможных изменений качества, о котором говорил Аристотель. В этом отношении оно предвосхищает современное понятие интенсивной физической величины (противопоставляемое экстенсивным величинам — их Аристотель только и относил к количествам).

С другой стороны, то же учение, если сосредоточить внимание на самом процессе интенсии или ремиссии, предвосхищает другое современное понятие — переменной величины.

Сразу отметим, что упомянутые выше Гайденко и Смирнов обратили внимание преимущественно на этот второй аспект и поэтому у них в книге [5] учение об интенсии и ремиссии качеств фигурирует под рубрикой средневековой кинематики. Но ведь первый аспект с позиций истории информационной сферы имеет не меньшее значение.

Кроме того, хотя кинематика, т. е. исследование понятия скорости движения, и была частью учения об интенсии и ремиссии качеств, но в рамках этого учения рассматривались и такие процессы, как потемнение, похолодание, сгущение и т. п.

По-видимому, можно сблизить первый аспект учения об интенсии и ремиссии качеств (связанный с практической проблемой градуировки степеней качества) с учением о широте форм как более абстрактной, философской постановкой той же проблемы. Что касается второго аспекта учения об интенсии и ремиссии качеств (связанного с изучением процесса изменения качества), то его предшественником и «философским двойником» в какой-то степени явилось учение о текущей форме и течении формы.

Итак, можно сосредоточить наше внимание на учении об интенсии и ремиссии качеств, считая, что два других упомянутых учения являются отчасти его «философскими двойниками», а отчасти предшественниками.

Целесообразно еще сказать несколько слов о предыстории этого учения. Как было видно из сказанного ранее, уже Аристотель размышлял об изменчивости качеств и постоянно говорил об их промежуточных степенях. Однако он в своей «Физике» категорически отверг возможность градуировки этих промежуточных степеней, заявив:

«Ни качественное изменение, ни рост, ни возникновение не равномерны, а таково только перемещение».

Своеобразно отразилось представление о постоянных и меняющихся сущностях в классификации дисциплин квадривиума по Боэцию. У него арифметика и геометрия определялись соответственно как науки, занимающиеся постоянными множествами и величинами, а музыка и астрономия — изменяющимися множествами и величинами.

Как было сказано выше, в разд. 3.4, великий таджик ИбнСина изучал различия между величиной покоящейся (по-латыни quantitas quieta) и величиной текущей (quantitas diffluens).

Занимался этим также Ибн-Рошд, который обозначал изменяющееся качество термином, звучащим на латыни как forma mutata (или forma mota).

Стандартные для последующей философии термины forma fluens и fluxus formae появились у Альберта Великого [ 18, с. 147].

Как отметил Н. И. Стяжкин в [14], некоторый вклад в развитие понятия переменной величины внес Дунс Скот.

И теперь, наконец, мы подошли к тому новому, что сделали в исследовании этой проблемы ученые XIV века, работавшие главным образом в Мертонском колледже Оксфорда.

Это — Томас Брадвардин (1290—1343), Уильям Хейтсбери, Ричард Свайнсхед (фамилии встречаются в разных транскрипциях, в частности, Свайнсхеда часто называют Суисет), Джон Дамблтон. Особо заслуживает внимания парижанин Николай Орем, или Орезм (1323—1382), автор замечательного трактата «О конфигурации качеств» [30].

Ученых Мертонского колледжа называли калькуляторами, поскольку они в своих рассуждениях активно пользовались вычислениями. Количественно степень проявления какого-либо качества они выражали в градусах (т. е. ступенях). Если некоторое качество отсутствовало, это был «не-градус»; если оно присутствовало в максимальной степени, это был «высший градус»; промежуточной степени соответствовал «средний градус широты».

Наряду с интенсивностью какого-либо качества (выражавшейся в градусах) они рассматривали его экстенсивность. Так, интенсивностью движения была его скорость, а экстенсивностью — время движения.

Мертонцы уже свободно пользовались понятием скорости движения. При этом, наряду с униформным (по-нашему — равномерным) движением, они изучали дифформное (неравномерное) движение. Более того, они даже имели понятие обуниформно-дифформном, т. е. «равномерно неравномерном» (в нашей терминологии — равноускоренном или равнозамедленном), движении.

Конечно, нашего понятия мгновенной скорости неравномерного движения как производной пути по времени у них быть не могло, и они обходили эту трудность, определяя мгновенную скорость в какой-либо момент времени как скорость такого движения, которое было бы равномерным начиная с этого момента.

По-видимому, высшим достижением мертонцев считается теорема о том, что путь, проходимый «униформно-дифформно» движущимся телом за некоторое время, равен пути, которое прошло бы тело за то же время, если бы двигалось «униформно» со средней скоростью.

Смысл этой теоремы ясен из рис. 3.3, на котором v (t) — мгновенная скорость равноускоренного движения, v_cp — средняя скорость движения, а проходимым путям соответствуют площадь трапеции, ограниченной линией v (t), и равная ей площадь прямоугольника, ограРис. 3.3. К теореме о средней скорости.

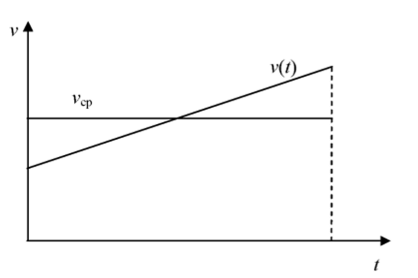
ничейного линией v_cp.

Мертонцы проводили другие довольно тонкие рассуждения, касающиеся отстояний того или иного градуса от различных возможных точек отсчета [5, с. 290—294], доказывали соответствующие теоремы, но не говорили ничего о реальных методах измерения. В частности, они как будто не видели трудностей, связанных с возможным отсутствием физической аддитивности.

В связи с этим знаток средневековой науки Аннелизе Майер назидательно заметила:

«…Это является как раз весьма существенной чертой схоластического естествознания… считают до того, как могут измерить» [26, с. 281].

Как было показано в гл. 2, эта «существенная черта» была свойственна еще Аристотелю, который в своей теории движения спокойно удваивал или делил пополам неизвестно что. Но ее легко обнаружить и в современной науке.

Вспомним, например, как Клод Шеннон ввел понятие количества информации. Он сначала потребовал, чтобы количество информации в двух независимых сообщениях было суммой количеств информации в каждом из них, и отсюда уже получил формулу, позволившую (косвенным образом, по статистическим оценкам вероятностей) измерить информацию. Поэтому совершенно прав А. В. Ахутин, возражающий А. Майер следующим образом:

«…Исследование отношений вообще предшествует понятию мерной единицы, которая выделяется как некий всеобщий измеритель из уже развитой системы отношений. До тех пор, пока этого не сделано, конструирование объекта возможного измерения и соответствующей процедуры не может вестись иначе, чем в терминах качества, отношения, сопоставления, формирующих понятия тождества и равенства» [26, с. 138].

Правда, следовало бы уточнить: «понятий тождества и равенства» в системе объектов совершенно недостаточно для формирования полноценной измерительной ситуации (напомним о предизмерительных ситуациях, которые рассматривались в разд. 1.4); однако для историка Ахутина хороша уже и такая не вполне точная формулировка.

Чрезвычайно интересным представляется вопрос о том, каким виделось мертонцам соотношение между количествами, с одной стороны, и степенями качеств (интенсивностями) — с другой. С этой точки зрения важна следующая мысль Свайнсхеда:

«Если некоторое количество больше отличается от нуля (nonquanto), чем другое количество, то оно называется большим; отсюда точно так же, если нечто дальше отстоит от не-градуса своей интенсивности, то оно называется более интенсивным» [5, с. 293].

Здесь ясно выражена аналогия (а следовательно, различие?): то нечто, которое характеризуется интенсивностью, ведет себя похоже на количество (которое представляет собой либо конечное множество, либо экстенсивную величину), но всё же, видимо, чем-то отличается от количества.

Вместе с тем в работах мертонцев можно найти и утверждения о соподчинении этих понятий, например: «Всякая широта есть некое количество» [Там же, с. 325]. Таким образом, создается впечатление, что мертонцы колебались в вопросе о соотношении понятий экстенсивных и интенсивных свойств — между ними должна быть то ли только аналогия, то ли общность.