Численное решение некорректных задач. 
Поиски минимума

Определение некорректной задами

Проблемы, которым посвящена данная глава, встречаются, как правило, при необходимости решения обратных или плохо обусловленных задач. Разработке методов решения некорректных задач и их обоснованию посвящена обширная литература^[1].

Некорректные задачи встречаются в геофизике (задачи гравиметрии, обратная задача теплопроводности), медицинской диагностике (обработка данных томографии головного мозга), сейсмологии, диагностике плазмы, экспериментальной астрофизике, криминалистике (восстановление фотоизображений) и во многих других областях.

Понятие некорректно поставленной задачи было введено Ж. Адамаром при изучении проблемы постановки граничных условий для различных типов дифференциальных уравнений в частных производных.

Запишем дифференциальную задачу в общем (операторном) виде:

где и е U; f е F; U, F — функциональные пространства; L — оператор (действующий из пространства U в пространство F). Пусть А/ — погрешность в определении правой части /, /* — точная правая часть, м° — точное решение исходной задачи.

Определение 9.1. Задачу (9.1) назовем корректно поставленной (корректной), если:

• 1) ее решение существует и единственно;
• 2) решение задачи устойчиво по правым частям, т. е. для любого 8 существует е (8), такое что из р/-(У,/О - 8 следует р_L,(u, м°) < е, где е (8) может быть сколь угодно малым за счет выбора малого 8.

Задачи, не удовлетворяющие этим требованиям, являются некорректно поставленными (или некорректными).

Классическим примером некорректно поставленной задачи является пример Лдамара^х:

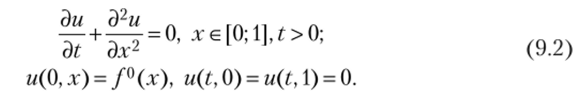
Решение этой же задачи, но с возмущенными начальными данными представим в явном виде:

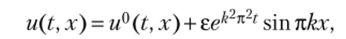
где 8 — малое число, a u°(t, х) — решение исходной задачи. То, что функция u (t, х) — решение, проверяется непосредственной подстановкой. Видно, что при большом числе k возмущение может неограниченно возрастать. Эту задачу можно сделать корректной, если ввести определенные ограничения на правые части или решение. В этом состоит смысл некоторых подходов к решению некорректных задач, о чем речь пойдет далее.

Например, если предположить, что правая часть задачи (9.1) (или начальное распределение в обратной задаче теплопроводности (9.2)) /(х) является гладкой функцией, то задача может оказаться корректной. Это предположение представляется вполне разумным, поскольку начальное распределение температуры, например, в недрах Земли, является гладкой функцией. Следовательно, гипотеза о превращении обратной задачи теплопроводности в корректную путем сужения допустимого класса функций / вполне реальна. К сожалению, погрешности при измерениях или машинные ошибки выводят / из пространства F.

Еще одним классическим примером некорректной задачи является интегральное уравнение Вольтерры первого рода^[2][3]

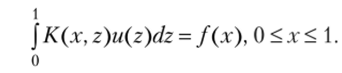
В задачах восстановления сигнала искомой функцией является первичный сигнал, f (x) — функция, значения которой измеряются приборами, К (х, z) — известное гладкое ядро, или аппаратная функция. Преобразование вида.

обычно является сглаживающим, т. е. преобразующим негладкую функцию и в гладкую /. Действительно, преобразования двух функций и (х) и и (х) + + sinrcfct' отличаются на функцию следующего вида: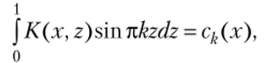

где Ck (x) — k-и коэффициент Фурье функции К (х, г). Известно, что коэффициенты Фурье гладкой функции убывают с ростом k тем быстрее, чем более гладкой является сама функция. Это означает, что преобразование Ku=f отображает большое пространство U негладких функций и (х) в очень малое пространство гладких функций/. Но интересующее нас обратное преобразование вида и = К ^xf_y очевидно, обладает противоположными свойствами, поскольку отображает малое функциональное пространство в большое, что и является причиной некорректности задачи. Это ясно из сравнения заметно отличающихся решений и (х) и v (x) = и (х) + A sinner интегральных уравнений:

с мало различающимися правыми частями при достаточно большом k. Малые высокочастотные возмущения в правых частях вызывают заметные различия в решении.

При численном решении соответствующей дискретной задачи, полученной из исходной путем аппроксимации интеграла квадратурными формулами, мы получим плохо обусловленную систему линейных алгебраических уравнений (СЛАУ) и сильно осциллирующую с ростом количества расчетных узлов по х сеточную функцию.

Один из известных содержательных примеров интегрального уравнения, являющегося некорректно поставленной задачей, — обратная задача гравиметрии. Она заключается в определении формы залежей руды под поверхностью Земли по аномалии напряженности силы тяжести Ag, измеренной на земной поверхности.

Предположим, что среда, находящаяся под поверхностью Земли (z = 0), состоит из масс с известными плотностями и р₂, разделенных контактной границей z (x). Пусть эта граница z (x) = -Н всюду, кроме отрезка [а; /, на котором z (x) = -Н + z (x), где z (x) подлежит определению. Эта задача в итоге сводится к решению интегрального уравнения следующего вида:

Можно показать неустойчивость решения z (x) относительно малых возмущений правой части этого уравнения.

• [1] Приведем некоторые из книжных публикаций: Федоренко Р. П. Указ, соч.; Тихонов А. Н., Арсенин В. Я. Методы решения некорректных задач. М.: Наука, 1986; Калиткин Н. Н. Численные методы. СПб.: БВХ-Петербург, 2011; Самарский А. А., Вабищевич П. Н. Численныеметоды решения обратных задач математической физики. М.: URSS, 2004; Тихонов А. Н., Гончаровский А. В. Некорректные задачи естествознания. М.: Изд-во МГУ, 1987.
• [2] Владимиров В. С. Уравнения математической физики. М.: Наука, 1981.
• [3] Там же; Марчук Г. И. Методы вычислительной математики. М.: Наука, 1989.