Производные по времени

Пусть в пространстве задана некоторая величина, зависящая от координат и времени, представляемая функцией F (r, t) (это может быть, к примеру, температура воздуха), и пусть наблюдатель движется по некоторой траектории и фиксирует через определенные промежутки времени значения величины F в том месте, где он находится. Очевидно, для него величина F будет функцией времени: F= F (t). Как, зная функцию F (r, 1), траекторию и скорость наблюдателя, найти скорость изменения величины F с точки зрения движущегося наблюдателя, т. е. производную dF/dfl

В момент времени t наблюдатель находится в точке г и фиксирует значение F (t)= F (r, t). В момент времени t + dt он окажется в точке г + dr и зафиксирует значение F (t + d/)= F (r +dr, t + d/). Разность этих двух значений будет равна.

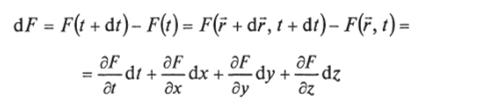
(по определению частных производных). Введем с помощью векторного оператора V скалярный оператор

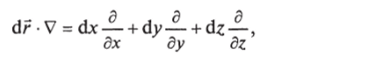
тогда полученный результат можно представить в виде 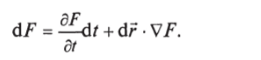Деля это выражение на dt, окончательно получаем.

или, учитывая, что dr/dT — скорость v наблюдателя,.

д д д.

Здесь скалярный оператор v-V = v — + v — + v —. Первое слагае;

^х дх «ду ^г dz

мое в правой части (5.15) учитывает изменение F со временем в данной точке, второе — смещение наблюдателя в точку с другим значением F.

Задача 5.9. Плотность воздуха в атмосфере меняется с высотой.

*.

по закону р = р₀е ^м (см. задачу 5.5). Аэростат поднимается вертикально вверх со скоростью 5 м/с. С какой скоростью меняется плотность воздуха в гондоле аэростата?

Решение. Ось z направим вертикально вверх, h = z- Имеем: р(г, t) = р₀е" ^г/". Формула (5.15) дает.

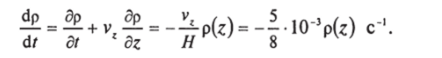
(Было учтено, что производные по х, у равны нулю, функция р от времени не зависит.) Знак минус соответствует тому, что плотность со временем убывает.

Задача 5.10. Скорость ветра задается векторным полем v = v (r, t). Наблюдатель на воздушном шаре движется вместе с потоком воздуха. Каково ускорение наблюдателя?

Решение. Скорость наблюдателя в любой точке и в любой момент времени равна скорости ветра в этой точке в этот момент времени, т. е. определяется функцией v (r, /). Формула (5.15) дает.

В компонентах:

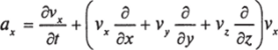
и т. д.

Рассмотрим теперь другую проблему. Имеется замкнутая поверхность S, и пусть эта поверхность движется. Скорость точек поверхности v для разных точек может быть разной, так что поверхность, вообще говоря, деформируется. В пространстве задана некоторая величина, представляемая функцией F (r, t). В момент времени t поверхность занимает определенное положение и охватывает объем V.

Рассмотрим интеграл jV (r,/)dF. Как изменится этот интеграл за.

V

малое время dr?

Если поверхность неподвижна, интеграл изменится за счет того, что меняется функция F:

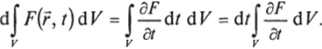
Если функция Fне меняется со временем, но поверхность смещается, интеграл изменится за счет изменения области интегрирования. Рассмотрим положение поверхности на момент времени t. Пусть d5 — элемент поверхности с нормалью и и скоростью v. За время dt элемент сместится на вектор vd;, заметая объем v • й d5dr (см. формулу (5.3)). В результате интеграл получит приращение.

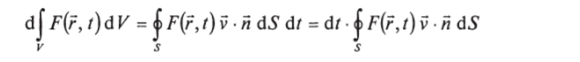
(см. аргументацию при получении формулы (5.8)).

Для общего случая, когда меняются и функция, и поверхность, объединяя эти два результата, будем иметь.

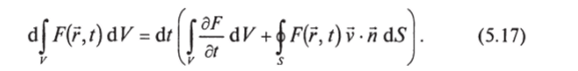
Отсюда для скорости изменения интеграла получаем.

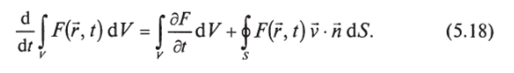
Задача 5.11. В условиях задачи 5.9 найти скорость изменения массы воздуха в гондоле аэростата. Для простоты будем считать, что гондола представляет собой вертикально ориентированный цилиндр высотой / и сечением S.

Решение. Используем формулу (5.18). Роль плотность воздуха: F (F, /)= р (^) = р₀ ехр -^Л Плотность не за висит от времени. Имеем:

функции F играет. Плотность не за;

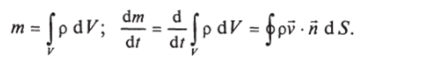
Гондола движется как твердое тело, и скорость всех точек поверхности одинакова и направлена вверх. Поверхностный интеграл разобьется на сумму интегралов по днищу, потолку и боковой поверхности. Пусть в момент времени / днище находится на высоте z, тогда потолок будет на высоте z + /? Плотность воздуха на дне р (г),.

на потолке р (г + /) = р (г)+ — / = р (г)—— р (г)/ (разложение.

dz Н

функции в окрестности точки г). На потолке v • й = v, на дне v • й = -v (на дне нормаль к поверхности направлена вниз), на боковой поверхности v • й = 0, так как векторы скорости и нормали на боковой поверхности ортогональны. Таким образом, остаются лишь интегралы по днищу и крышке цилиндра. Учитывая, что во всех точках дна и крышки подынтегральная функция постоянна, получаем.

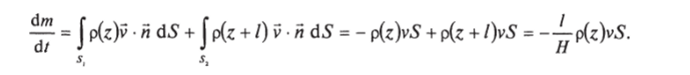
Производная отрицательна, что соответствует убыли массы. Должно быть ясно, что уменьшение массы воздуха в гондоле связано с уменьшением плотности с высотой.