Законы сохранения. 
Физика. 
Механика. 
Электромагнетизм

Замкнутой системой называется система, на которую не действуют внешние силы. Если система замкнута, то ее энергия, импульс и момент импульса не изменяются со временем.

Формально сохранение импульса следует из формулы (3.3), сохранение энергии — из формулы (3.30), сохранение момента импульса — из формулы (3.36), т. е. в конечном итоге указанные законы сохранения следуют из трех законов Ньютона.

Однако эти законы на самом деле более фундаментальны, чем законы Ньютона. Они являются следствиями пространственно-временных симметрий.

Закон сохранения энергии является следствием однородности времени, сохранение импульса — следствие однородности пространства, сохранение момента импульса — следствие изотропности пространства.

Под однородностью времени понимается эквивалентность всех моментов времени, которая проявляется, например, в следующем. Пусть мы создали систему, функционирующую определенным образом. Предполагается, что если воссоздать такую же систему через, скажем, тысячу лет, то она будет при прочих равных условиях функционировать точно так же. Перенос во времени не влияет на функционирование системы. Однородность и изотропность пространства мы уже обсуждали. То, что перечисленные законы сохранения следуют из законов Ньютона, свидетельствует в пользу законов Ньютона, а не законов сохранения. Имеются ситуации, которые не могут быть описаны в рамках ньютоновской механики, и тем не менее для них выполняются обсуждаемые законы сохранения.

Итак, для замкнутой системы справедливы следующие положения.

1) Сохранение энергии:

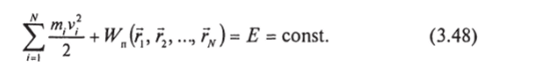
Здесь W_n — потенциальная энергия системы, зависящая от координат частиц, составляющих систему. Если внутренние силы не потенциальны, мы, строго говоря, выходим за пределы механики. Работа непотенциальных внутренних сил переводит механическую энергию в другие виды энергии, например в тепло. В этом случае, хотя энергия в широком смысле слова сохраняется, механическая энергия не сохраняется.

2) Сохранение импульса:

3) Сохранение момента импульса:

Возникает естественный вопрос: существуют ли замкнутые системы? Ясно, что в земных условиях мы не имеем замкнутых систем, поскольку нельзя избавиться от сил тяжести. Вообще, любая система гравитационно взаимодействует со всей Вселенной и поэтому не является замкнутой. Однако, с другой стороны, мы видели, что свободно падающая в гравитационном поле невращающаяся система отсчета не слишком больших размеров является инерциальной. От гравитационного взаимодействия со всей Вселенной можно избавиться, перейдя в свободно падающую систему отсчета. Это уникальная особенность гравитационного взаимодействия. И тогда любая механическая система в такой свободно падающей системе отсчета может с хорошей точностью рассматриваться как замкнутая. Например, космический корабль со всем содержимым, рассматриваемый в сопутствующей невращающейся системе отсчета, является замкнутой системой, для которой справедливы все перечисленные законы сохранения. (Деятельность космонавтов является примером непотенциальных внутренних сил, работа которых может изменить механическую энергию системы, но которые не могут изменить импульс и момент импульса системы.).

Так или иначе, условие замкнутости системы — это серьезное ограничение применимости законов сохранения, однако на самом деле это условие можно ослабить. Если части системы вступают в кратковременное сильное взаимодействие (например, столкновение), а внешние силы и их моменты таковы, что за время взаимодействия частей не успевают заметно изменить импульс и момент импульса системы, закон сохранения импульса и момента импульса может использоваться для определения того, как перераспределяются эти величины между взаимодействующими частями системы. Например, если пуля попадает в летящую утку, то хотя система пуля—утка не замкнута (действуют силы тяжести, утка машет крыльями), закон сохранения импульса и момента импульса позволяет определить, как импульс и момент импульса пули распределятся между частями этой системы сразу после попадания.

Важное замечание. Формулы (3.48)—(3.50) нерелятивистские. Для релятивистских систем сформулировать аналогичные законы по ряду причин, в которые здесь не место углубляться, не так просто. Однако для столкновений частиц можно сформулировать простые законы сохранения энергии и импульса.

Пусть в некоторую малую область пространства входит несколько частиц, и через малое время выходит несколько частиц (не обязательно тех же и такое же количество). Что происходит внутри области, нас не интересует. Такой процесс будем называть столкновением. Для столкновения имеют место следующие равенства:

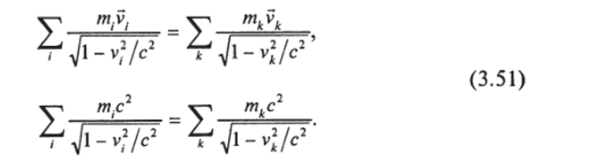
Суммы слева — по всем частицам до столкновения, справа — после. Первое из этих равенств выражает закон сохранения импульса, второе — энергии.

Задача 3.17. Две частицы массами m_v m_v соединенные пружиной с жесткостью к длиной а, движутся в поле тяжести. Каков самый общий вид движения этой системы?

Решение. Рассматриваемая система — это гантель, движение которой в поле тяжести было описано в задаче 3.14. Отличие лишь в том, что расстояние между частицами может меняться. Легко видеть, что на движении центра масс гантели это обстоятельство не сказывается. Таким образом, центр масс системы движется по параболе. Перейдем в систему центра масс. Эта система отсчета инерциальна, центр масс гантели в ней неподвижен и находится в начале координат, внешние силы отсутствуют, система замкнута, и выполняются все законы сохранения.

Центр масс, как мы уже видели, лежит на отрезке_; соединяющем частицы, поэтому возможное движение системы — вращение прямой, на которой лежат частицы, и изменение расстояния между частицами. Система характеризуется энергией Е, моментом импульса.

L и импульсом Р = 0. Все эти величины сохраняются (не изменяются со временем). Момент импульса системы (см. задачу 3.13).

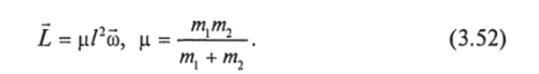
Здесь /— расстояние между частицами, величина р называется приведенной массой. Частицы движутся в плоскости, ортогональной.

Внутренние силы в системе осуществляются пружиной, и эти силы потенциальны. Потенциальная энергия пружины равна вектору Z, и постоянство этого вектора означает, что плоскость, в которой вращается гантель, не изменяется. Пусть это будет плоскость хОу. Вводя полярные координаты (см. п. 2.2.9), для момента импульса получим.

W_n =k (lа)²/2, или, в терминах равенства (3.48),.

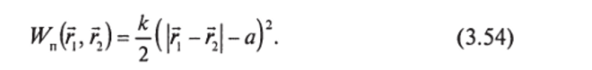
Равенство (3.48) дает.

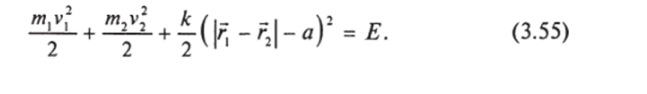
В полярных координатах это равенство примет вид (см. формулу (2.172)).

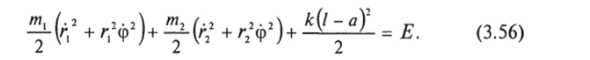
При этом /=/•, + г₂. Учитывая (см. задачу (3.12)), что.

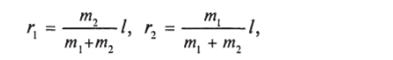
равенство (3.56) можно представить в виде или, заменяя ф с помощью равенства (3.53), Полагая х = I — а, приведем это уравнение к виду.

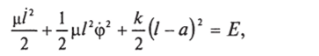
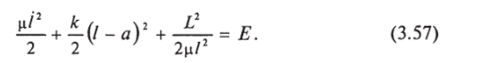
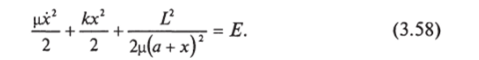
Уравнение (3.58) соответствует одномерному движению с потенциальной энергией.

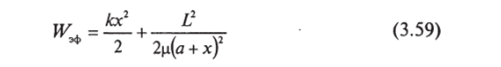
(см. п. 2.2.8) и, в принципе, может быть проинтегрировано. Отсюда найдется / = 1(1). Подставляя эту функцию в формулу (3.53), найдем функцию <�р = ф (Г).

Если L = 0 (гантель не вращается), из уравнения (3.58) находим.

Полагая со = х₀ = ^2Е/к, приведем это равенство к виду.

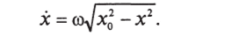
Как решаются такие уравнения, мы видели (см. п. 1.2.5.). Пишем:

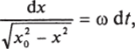
откуда, интегрируя, находим.

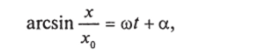
где, а — постоянная интегрирования, зависящая от начальных условий. Окончательно имеем.

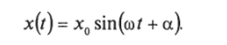
Это уравнение гармонических колебаний. Таким образом, расстояние между частицами в этом случае меняется по закону.

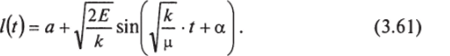
Если L * 0, но амплитуда колебаний х₀ много меньше а, второе слагаемое в правой части равенства (3.59) можно считать постоянным. В этом случае мы снова получим равенство вида (3.60), но вместо величины Е в нем будет стоять Е' = Е — Ь^г/2ш^г, которая и войдет в выражение для амплитуды колебаний. В этом случае гантель вращается с угловой скоростью Ф = L/ia² (см. формулу (3.53)), и расстояние между частицами меняется согласно формуле (3.61), в которой вместо Е нужно подставить Е'.

Задача 3.18. В шар, неподвижный относительно инерциальной системы отсчета (рис. 3.3), попадает пуля и застревает в нем. Как будет двигаться шар после этого? Какова работа внутренних сил?

Решение. Пусть R — радиус шара, М — его масса, т — масса пули. Центр шара — в начале координат, пуля движется в плоскости хОу вдоль прямой у = b (напомним, величина b называется прицельным параметром) со скоростью v = -V/. За счет.

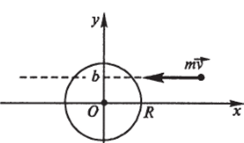
Рис. 3.3.

? вращения вокруг своей продольной оси пуля обладает собственным моментом импульса S = - Si. Рассмотрим систему пуля—шар. Сохраняющиеся величины — импульс и момент импульса. Силы взаимодействия между пулей и шаром не потенциальны, поэтому механическая энергия не сохраняется, часть энергии переходит в другие виды (в конечном итоге — в тепло).

Начальный импульс системы Р_х = mv = -mvi (это импульс пули).

Импульс системы после столкновения Р₂ = (М + т) V, V — скорость центра масс шара и застрявшей в нем пули. Сохранение импульса дает равенство.

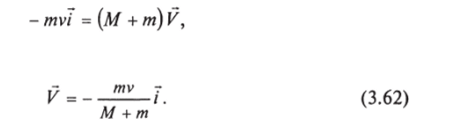
откуда находим.

Обратите внимание. Импульс системы определяется массой системы и скоростью центра масс. Сохранение импульса означает, что взаимодействие частей системы не изменяет скорости центра масс. Мы вообще могли игнорировать столкновение, а просто найти скорость центра масс системы пуля—шар по формулам (3.12), (3.15). Сделайте это и убедитесь, что получится формула (3.62). Заодно найдете, что центр масс движется по прямой у = mb/(m + М).

Формула (3.62) не определяет, однако, всего движения. Система будет еще вращаться вокруг центра масс. Для определения вращения обратимся к закону сохранения момента импульса.

Начальный момент импульса системы — это момент импульса пули, определяемый по формуле (3.38). Для орбитального момента пули находим.

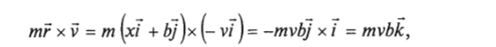
так что момент импульса системы равен.

После столкновения момент импульса системы представится суммой орбитальных моментов шара и пули при их вращении вокруг общего центра масс (это момент импульса гантели, см. задачу 3.13) и собственного момента вращающегося шара (см. задачу 3.16). Пусть <�о — угловая скорость вращения гантели. Очевидно, угловая скорость шара будет такая же (когда гантель сделает один оборот, шар также сделает один оборот). Сохранение импульса дает равенство.

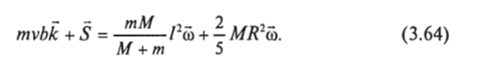
Здесь / — расстояние между центром шара и застрявшей в нем пулей. Это расстояние зависит от деталей проникновения пули в шар и не может быть определено по заданным условиям. Во всяком случае оно не больше радиуса шара. Если масса шара много больше массы пули, первое слагаемое в правой части (3.64) много меньше второго, и для угловой скорости получим.

Если 6 = 0 (пуля попадает в центр шара), шару передастся только собственный момент пули. Момент импульса, как и импульс, неуничтожим. Если шар впоследствии перестанет вращаться из-за взаимодействия с другими телами, момент передастся этим телам.

Что касается энергии, то начальная энергия системы — это кинетическая энергия пули mv²/2 (строго говоря, нужно было бы учесть и энергию вращения пули, но она много меньше указанной величины). Конечная энергия — это энергия поступательного движения (т + М) V²/2 и энергия вращения системы пуля—шар. Энергию вращения сосчитать не так просто. Далее мы увидим, как это делается. Конечная энергия окажется меньше начальной. Разность — это и есть работа внутренних сил. Мы еще вернемся к этой проблеме.

Задача 3.19. Частица массой /и, с кинетической энергией W_K налетает на неподвижную частицу массой т₂ и сливается с ней в одну частицу. Определить массу и скорость получившейся частицы. Кинетическая энергия налетающей частицы соизмерима с ее энергией покоя, массы частиц также соизмеримы.

Решение. Мы имеем дело со столкновением релятивистских частиц, для которого справедливы формулы (3.51).

Для начала выразим импульс частицы через кинетическую энергию. Исключив скорость из выражений для импульса и энергии частицы, получим.

Учитывая, что JV_K = Етс², получаем.

(это энергия системы до столкновения).

Обратите внимание. При столкновении сохраняется полная энергия системы, поэтому необходимо учитывать энергию покоя частиц!

Из уравнений (3.68), (3.69) находим.

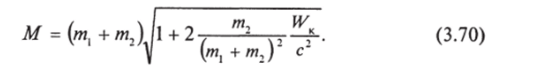
Как видим, масса составной частицы оказывается больше суммы масс исходных частиц! Часть кинетической энергии налетающей частицы переходит во внутреннюю энергию составной частицы, а масса объекта и есть мера его внутренней энергии. В нерелятивистском приближении, при W_K

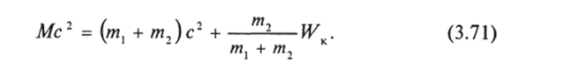
Пусть Л/ — масса составной частицы. Закон сохранения импульса с учетом формул (3.66), (3.67) дает равенство.

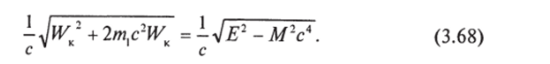
Здесь Е — сохраняющаяся энергия системы, равная.

Второе слагаемое в правой части этого равенства дает работу внутренних сил при столкновении частиц, которая переходит во внутреннюю энергию составной частицы. (Получите этот результат непосредственно, см. предыдущую задачу.).

Обратите внимание. В нерелятивистской механике мы имеем отдельно закон сохранения массы и закон сохранения энергии. Баланс энергии производится отдельно. Если сталкивается несколько тел, одно из которых — граната, то кинетическая энергия получившихся продуктов столкновения будет больше кинетической энергии исходных тел. Для баланса энергии мы должны учесть энергию, выделяющуюся при взрыве гранаты, что выводит нас за пределы механики. При релятивистском подходе энергия взрывчатки уже учтена в массе гранаты.

Что касается скорости составной частицы, то из выражений для импульса и энергии частицы следует, что.

Учитывая формулы (3.67), (3.69), для скорости частицы получаем.

При Ж получим V -> с, как и должно быть. В нерелятивистском пределе, при малых получим.

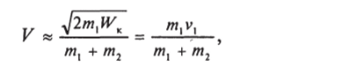
в согласии с соответствующим результатом предыдущей задачи.

Задача 3.20. Частица массой т со скоростью v (v «с) сталкивается с такой же неподвижной частицей. Столкновение упругое. (Наглядная картина — столкновение бильярдных шаров.) Найти скорости частиц после столкновения.

Решение. Упругое столкновение — это столкновение, при котором сохраняется кинетическая энергия системы. При столкновении, например, хороших бильярдных шаров в момент их остановки кинетическая энергия переходит в потенциальную энергию упругой деформации шаров, которая далее снова переходит в кинетическую энергию разлетающихся шаров. Однако полностью упругих деформаций не бывает. Упругое столкновение макроскопических тел — это некоторая идеализация. Тем не менее настоящие упругие столкновения бывают. Это столкновения атомов или еще меньших частиц. Дело в том, что внутренняя энергия частиц атомного масштаба может принимать лишь определенные значения (квантуется). Если энергии столкновения недостаточно для перевода частицы на более высокий энергетический уровень, ее внутренняя энергия не может измениться и столкновение будет упругим.

Сохранение импульса дает равенство.

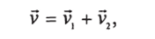
сохранение энергии —.

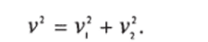
Возводя первое из этих равенств в квадрат, получим откуда, сопоставляя со вторым, находим.

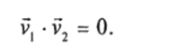
Это означает, что-либо один из сомножителей — нулевой вектор, либо векторы скоростей разлетающихся частиц ортогональны (бильярдные шары разлетаются под прямым углом). Первый случай реализуется при центральном столкновении, когда налетающий шар останавливается, а неподвижный приобретает скорость налетевшего. Нельзя сказать, чтобы эти результаты были очевидными.

Как видим, законы сохранения, помимо того, что это фундаментальные законы природы, являются эффективным средством получения важных и неочевидных результатов. Эта эффективность связана с тем, что их применение избавляет от необходимости отслеживать детальный механизм явления, который часто вообще остается неизвестным. Проект вечного двигателя можно отвергать с порога, не вникая в детали. «Этого не может быть, потому что этого не может быть никогда» — именно такова логика аргументации на основе законов сохранения. Внутренние силы не могут изменить движение центра масс системы. Внутренние силы не могут изменить момент импульса системы.

Правда, эффективность применения этих законов существенно ограничивается требованием замкнутости системы. Как уже отмечалось, в земных условиях мы практически не имеем дела с замкнутыми системами. Однако требование замкнутости можно ослабить.

Обратимся к формуле (3.3). Пусть п — единичный постоянный вектор. Умножим равенство (3.3) скалярно на вектор п:

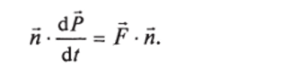
Поскольку п — постоянный вектор, его можно завести под знак производной:

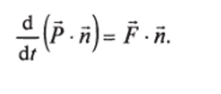
Величины Р_п = Р п, F_n = F п есть проекции векторов импульса и силы на направление, задаваемое вектором й. Таким образом,.

Скорость изменения проекции импульса на некоторое направление равна проекции силы на это направление.

Из формулы (3.74) следует, что если F_a = 0, то = 0, Р_п = const.

Если проекция суммарной силы, действующей на систему, на некоторое направление все время равна нулю, проекция импульса на это направление сохраняется:

Это означает, например, что если на все части системы действуют только вертикальные силы, проекция импульса на горизонтальную плоскость не изменяется.

Аналогично из уравнения (3.36) получим.

Скорость изменения проекции момента импульса системы на некоторое направление равна проекции суммарного момента сил на это направление.

Если проекция момента сил на некоторое направление равна нулю (момент сил относительно некоторой оси равен нулю), сохраняется проекция момента импульса на это направление (момент импульса относительно этой оси):

Уже отмечалось, что сохранение импульса и момента импульса связано с однородностью и изотропностью пространства. Ослабленные законы сохранения (3.75), (3.77) связаны с ослабленными требованиями однородности и изотропности: если пространство однородно в некотором направлении, сохраняется проекция импульса на это направление; если все направления, ортогональные некоторой оси, равноправны, сохраняется проекция момента импульса на эту ось. Сохранение энергии есть следствие однородности времени, но так как время одномерно, ослабленного варианта закона сохранения энергии нет: для сохранения энергии система должна быть замкнута.