Устойчивость плоской формы изгиба

Рассмотрим балку, нагруженную изгибающим моментом, действующим в вертикальной плоскости хОу (рис. 15.17). При большой жесткости в плоскости действия внешних сил, т. е. силовой плоскости, и малой жесткости во второй главной плоскости потеря устойчивости стержня может сопровождаться выходом из плоскости действия изгибающего момента. Такой вид потери устойчивости называется боковым выпучиванием.

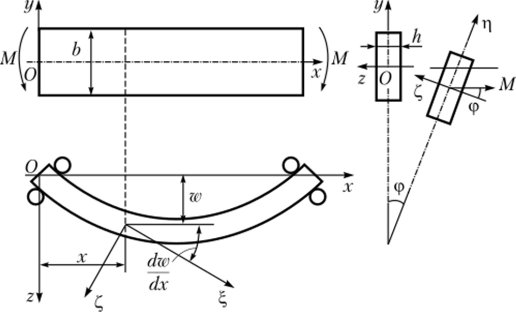
Рис. 15.17. Балка, нагруженная изгибающим моментом.

Положим, что момент инерции относительно главной центральной оси поперечного сечения Ог во много раз больше момента инерции относительно оси Оу.

Определим такое критическое значение момента М_кр, при действии которого наряду с плоской формой изгиба стержня будет существовать и другая форма, соответствующая боковому выпучиванию. Эта форма характеризуется соответствующими дополнительными перемещениями точек центральной оси в направлении оси Ог и повороту поперечного сечения вокруг оси Ох.

Допустим, что значение приложенного момента такое, что возникает боковое выпучивание стержня (см. рис. 15.17). Обозначим перемещения точек центральной оси в направлении осей Оу и Ог и угол поворота вокруг оси Ог символами v>w и ф соответственно.

Введем вспомогательную локальную координатную систему г|, С, начало которой совместим с центром тяжести сечения. Первые две оси направлены вдоль главных осей сечения, а третья — по касательной к упругой оси деформированного стержня. Значения кривизн оси деформированного.

d² v d²w

стержня в плоскостях ху и xz соответственно равны и В рамках допущения о малости угла поворота ф можно приближенно считать, что кривизны в плоскостях %г| и 4С будут равны тем же величинам. Кроме того, примем во внимание, что Л = 1_г п 1_Ц = 1_у.

Сделанные допущения дают возможность записать дифференциальные уравнения, определяющие деформированное положение стержня, в следующем виде:

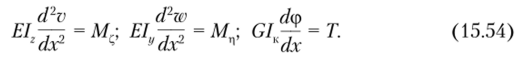
Спроецировав вектор-момент на локальные оси, определим входящие в уравнения (15.54) значения моментов:

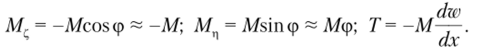
С учетом полученных результатов уравнения (15.54) запишутся в виде.

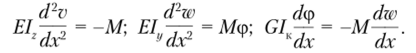
Первое уравнение тождественно уравнению (15.12), и его решение было рассмотрено ранее. Исключая перемещение гг" из второго и третьего соотношений, получаем еще одно уравнение второго порядка относительно ф:

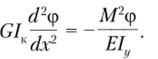
Используя обозначение.

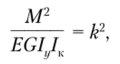
приходим к линейному дифференциальному уравнению второго порядка.

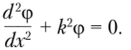
Решение уравнения ищем в виде ф = C, sinfcr + С, cosкх.

Согласно схеме закрепления концевые сечения стержня не закручиваются. Поэтому в качестве граничных условий примем.

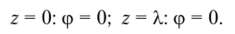
Таким образом, получена задача, тождественная рассмотренной ранее задаче Эйлера (см. формулы (15.14)—(15.18)). Принимая И = пп, находим минимальное значение критического момента М, соответствующее п = 1:

Для полученного решения найдем, что угол поворота изменяется вдоль оси бруса по синусоиде:

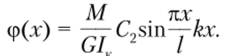
Используя метод приведения длины, как это делается для сжатых стержней, можно распространить полученное решение на другие виды закрепления балки.