Атомизм С. Пуассона и Ж. Фурье

Французская традиция атомизма была продолжена последователем Лапласа Пуассоном. Ф. Клейн так характеризует мировоззренческую позицию Пуассона: «Теоретически он был ортодоксальным сторонником атомистики в духе Лапласа»^[1]. Скажем несколько слов о том, что сделал Пуассон в области решения эллиптических интегралов. Напомним, что эта была традиционная область исследования для математиков эфирной традиции.

Пуассон рассмотрел циклические периоды v интеграла вида [, :

oVl-Z^[1]

«Здесь разность двух интегралов по путям / и /_1? соединяющим точки 0 и z, равна интегралу по замкнутому контуру, содержащему внутри две точки разветвления функции.^: -1 и +1. Не меняя значения последнего.

VI-г^[1]

интеграла, этот контур можно заменить двумя окружностями с центрами в указанных точках и соединяющим их отрезком действительной оси, дважды пробегаемым (рис. 1.33). Значение интеграла — период при положительном обходе этого контура — равно 2л"^[4].

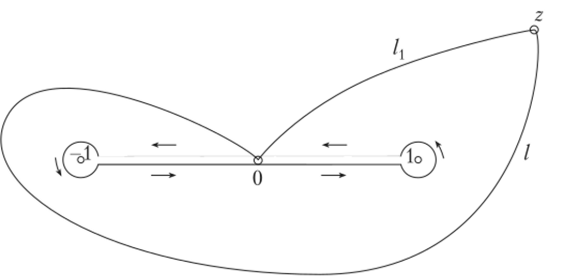
Рис. 1.33.

Т. 2. С. 166.

Теперь расскажем об одном из самых крупных атомистов XIX в. — Фурье. Получить элементарное образование и избежать безысходной бедности ему удалось благодаря бескорыстной заботе и поддержке мадам Моиттон. Она привлекла внимание епископа Осера к судьбе одаренного и вежливого мальчика и добилась его покровительства. По протекции епископа его приняли в Артиллерийскую школу при колледже бенедиктинцев. В поисках устойчивого положения Фурье несколько раз уходил и возвращался в аббатство бенедиктинцев и, наконец, в 1787 г. принял сан послушника и стал преподавать в том самом колледже, где начинал учебу. Он вел занятия по многим дисциплинами (математике, риторике, философии, истории), продолжая активно заниматься математикой.

Фурье прославился в физике своими фундаментальными работами по теории теплоты. Чтобы понять значение достижений Фурье в этой области, сделаем краткий обзор развития представлений о теплоте в Новое время. В теории теплоты, так же как и в теории электромагнитных взаимодействий, атомисты и представители эфирных теорий разделились на два непримиримых лагеря.

К атомистам относились Г. Галилей, Р. Бойль, И. Ныотон, П. Гассенди, Дж. Блэк, А. Лавуазье, П.-С. Лаплас и Ж. Фурье. Они понимали теплоту как течение некоторой особой невесомой жидкости, отличной от эфира. Эта жидкость состояла из частиц, между которыми действовали далыюдействуюгцие атомистические силы. Эта жидкость называлась теплород. Она проникала сквозь крупные тела и воздействовала на частицы этих тел. При этом между частицами теплорода действовали силы отталкивания, а между частицами теплорода и частицами крупных твердых тел — силы притяжения. Модель теплоты атомизма подразумевала перетекание теплоты из одного тела в другое подобно перетеканию жидкости. Из этого представления достаточно хорошо удавалось описать явления теплового баланса и теплопроводности.

«Физики по своим воззрениям на природу теплоты не единодушны. Большинство рассматривает теплоту как жидкость, которая по своей природе стремится расширяться и проникать в большей или меньшей степени в поры тел, в соответствии с температурой и тепловыми свойствами этих тел… Другие физики рассматривают теплоту как результат неразличимого движения молекул материи… Принимая в расчет принцип сохранения живых сил, можно дать определение: теплота есть живая сила, т. е. сумма произведений масс каждой молекулы на квадрат ее скорости»^[5].

Очевидно, что определение теплоты как живой силы воспроизводит определение живой силы, данное Лейбницем. Эфирные концепции относили к молекулярным и механическим, ибо частицы действовали непосредственно друг на друга, а не с помощью сил через пустоту. Эфирная традиция рассматривала теплоту как движение и соударение частиц. К представителям этой традиции следует отнести Р. Декарта, Р. Гука, И. и Д. Бернулли, Я. Германа, М. В. Ломоносова.

Кинетическая теория теплоты быстро столкнулась с серьезными сложностями, связанными с описанием теплоемкости. Ведь если представлять теплоту как движение молекул, то теплоемкость должна была быть пропорциональна плотности, т. е. чем больше масса тела, тем больше живой силы ему надо передать для нагревания. Но это противоречило опытам.

Вот как писал об этом Блэк: «Более плотные тела должны несомненно усиленнее передавать теплоту другим телам. Опыт учит в большинстве случаев прямо противоположному. Подобного рода мнения поэтому нельзя согласовывать с фактами»^[6]. Но эфирная концепция по своей сути не должна претендовать на описание нашего мира, ибо ее епархия — это иной эфирный мир. Ведь этот новый мир, по Декарту, подчинен совсем другим законам. Но об этом подробнее будет рассказано в главе, посвященной математике материального эфира.

Теперь попытаемся разобрать, какие новые идеи внес в теорию теплоты Фурье. Фурье исходил из представления о теплоте как о некотором потоке невесомой жидкости — теплороде. Этот поток теплорода пропорционален, по Фурье, разности температур. Но разность температур в предельном случае можно было выразить с помощью дифференциального уравнения в частных производных, т. е. через градиенты температуры. Представление о таком выражении разности разрабатывал атомист Лаплас. И именно в русле идей Лапласа продолжил работу Фурье.

Следующим важным достижением Фурье было различение процессов, происходящих внутри теплового потока и на его поверхности. Вследствие этого учета появляются различные уравнения, дополненные начальными условиями в явном виде. Фурье начал свои математические исследования там, где их закончил Лаплас. Лаплас использовал тригонометрический ряд с постоянными коэффициентами для разложения многочлена, но сферическим функциям.

Фурье предложил метод решения дифференциальных уравнений в частных производных через разложение прерывных и разрывных функций в ряды и интегралы Фурье. При этом он опирался на метод разделения переменных: «С помощью всех этих средств Фурье дал изображение большого числа функций, кажущихся по сравнению с ранее известными очень произвольными. Строгим доказательством общей приложимости своих методов к изображению функций Фурье не располагал, но он повсюду защищает верное само по себе утверждение, что с их помощью можно дать выражение „абсолютно произвольных функций“, т. е. таких функций, которые состоят из произвольных „частей“ закономерных функций; это положение он подтверждает многочисленными примерами»^[7].

Тригонометрические ряды использовались математиками XVIII в., но к началу XIX в. они были «в немилости» из-за неопределенности условий их сходимости. Поэтому Ж. Л. Лагранж сделал ставку на степенные ряды, пренебрегая тригонометрическими.

Но для атомизма вопросы сходимости не были столь принципиальными, ибо сходимость была требованием лейбницевской конечности решения дифференциального уравнения. А атомисты не были связаны такой метафизической установкой, они могли спокойно работать в области бесконечного. Поэтому Фурье свободно применил разложения в тригонометрические ряды и интегралы для решения задач распространения тепла в телах различной формы (кубе, цилиндре, сфере). Кроме того, атомизм вплотную подходит к явлениям нашего окружающего мира, поэтому выкладки Фурье могли быть отчасти проверены и экспериментально.

Работа «Аналитическая теория тепла» была закончена в декабре 1807 г. Экземпляры рукописи были разосланы на рецензирование Ж. Л. Лагранжу, П.-С. Лапласу, С. Ф. Лакруа и Г. Монжу. Только Монж поддержал идеи Фурье. Против публикации жестко высказался Лагранж, на которого не подействовали даже дальнейшие разъяснения Фурье.

Лагранж выступил против применения тригонометрических разложений Фурье. Основное возражение было выдвинуто против обоснованности сходимости этих рядов. Лаплас и Лакруа так и не заняли определенной позиции. Это привело к тому, что книга была опубликована только в 1822 г. О. Коши вскоре заметил, что уравнение теплопроводности Фурье совпадает с уравнением Навье в пределе малых скоростей. Много позже А. Фик построил теорию молекулярного переноса вещества, в которой основные уравнения совпали с уравнением Фурье с точностью до коэффициентов. Это были уравнения диффузии.

В связи с научной деятельностью Фурье следует рассмотреть новую для французского естествознания позицию. Эту позицию Ф. Клейн назвал феноменологической. Суть ее заключается в следующих словах Фурье: «Первопричины явлений нам неизвестны; но они подчиняются простым и постоянным законам, которые можно открыть путем наблюдения и изучение которых составляет предмет натуральной философии»¹.

Таким образом, Фурье не хочет явно говорить о своем атомизме и не хочет упоминать и эфирную традицию. Это отразило общую ситуацию в естествознании того периода. Эта ситуация абсолютного равенства сил. Это паритет между атомистом Лапласом и представителем эфирной традиции Лагранжем во Французской академии.

Ни атомисты, ни последователи эфира не могли говорить о своем превосходстве. И та, и другая позиция имела явные успехи, но и огромные трудности в объяснении явлений. Причем это не были трудности в описании явлений окружающего мира. Это были трудности с описанием явлений внутри теории.

Реальные явления не так важны для науки как таковой, которая оперирует абстрактными и идеальными объектами. Реальные явления важны для технических дисциплин, где без учета реальных процессов просто невозможно конструировать. Причем ситуация равенства между атомизмом и эфирной концепцией длилась уже более 200 лет. Поэтому нельзя было говорить, что время всех рассудит и выявит победителя. Именно такое реальное положение дел в науке конца XVIII — начала XIX в. и привело к возникновению кантовской «вещи-в-себе» в теоретическом разуме, а в дальнейшем и общей позитивистской установки всего естествознания.

• [1] Клейн Ф. Лекции о развитии математики в XIX столетии. М., 1989. С. 101.
• [2] Клейн Ф. Лекции о развитии математики в XIX столетии. М., 1989. С. 101.
• [3] Клейн Ф. Лекции о развитии математики в XIX столетии. М., 1989. С. 101.
• [4] Математика XIX века. В 3 т. / под ред. А. Н. Колмогорова, А. П. Юшкевича. М., 1981.
• [5] Спасский Б. И. Указ соч. Т. 1. С. 167.
• [6] Спасский Б. И. Указ соч. Т. 1. С. 168.
• [7] Клейн Ф. Указ. соч. С. 103—104.