Ортогональное планирование эксперимента

Структура матрицы С играет важную роль в реализации алгоритма определения коэффициентов аппроксимирующего полинома. Структура матрицы С зависит от выбора значений факторов в N опытах. Поэтому желательно особым образом выбирать значения факторов в опытах.

Элемент С" на главной диагонали матрицы С (i-я строка, L-й столбец) представляется суммой квадратов значений i-го столбца сочетаний факторов матрицы X в N опытах.

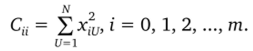
Элементы матрицы, симметрично расположенные относительно главной диагонали, равны между собой, т. е. матрица С — симметричная:

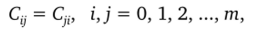
где первый индекс указывает номер столбца матрицы X, а второй индекс — номер строки.

При этом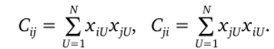

Чтобы существовала матрица С" ¹, матрица С размера (1 + т) х (1 + т) должна быть невырожденной, т. е. ее определитель должен быть отличен от нуля. Это условие выполняется, если все т —1−1 столбцов матрицы X линейно независимы. Кроме того, необходимо, чтобы число различных сочетаний факторов в матрице X (число опытов N) было не меньше, чем т + 1. Это условие исходит из того, что для определения т + 1 коэффициентов полинома необходимо не менее т + 1 уравнений (опытов).

Полученные коэффициенты В позволяют сформировать уравнение функции отклика при т + 1 членах уравнения. Если точность этого уравнения оказалась недостаточной, то требуется взять уравнение с большим числом членов и начать все заново, так как все коэффициенты В оказываются зависимыми друг от друга. Это возникает при использовании пассивного эксперимента. Однако если целенаправленно использовать активный эксперимент и особым образом построить матрицу сочетаний факторов в опытах X при планировании эксперимента, то коэффициенты полинома определяются независимо друг от друга.

Стратегия применения планов заключается в принципе постепенного планирования — постепенного усложнения модели. Начинают с простейшей модели, находя для нее коэффициенты и определяя ее точность. Если точность не удовлетворяет, то планирование и модель постепенно усложняются.

Задача планирования заключается в том, как строить матрицу X, чтобы матрица С легко обращалась и коэффициенты В определялись независимо друг от друга. Эти требования выполняются, если матрица С является диагональной, т. е. все элементы, расположенные не на главной диагонали матрицы, равны нулю.

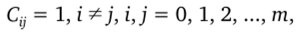
или.

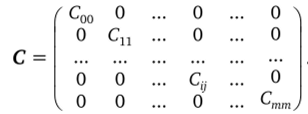
Тогда обратная матрица определяется как.

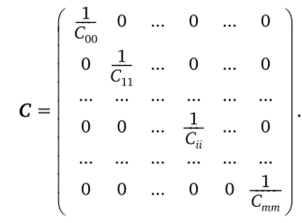
В этом случае система уравнений распадается на т + 1 независимых уравнения и коэффициенты полинома определяются как.

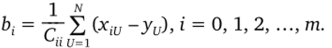
N ₂

Если учесть, что C_ti = Y, ^хш> ^то коэффициенты о= 1.

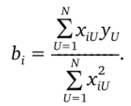
Требование выполнения условия С,-, = = 0 заключается в выполнении условия.

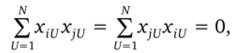
где i, j — номера столбцов в матрице X; i, j = О, 1, 2,т, при i *j.

Каждый столбец матрицы X можно представить в виде вектора.

N.

если Х, Х_; =? ^xiu^xju ~ О, то это означает, что скалярное про;

0=1.

изведение двух векторов X, и Х_; равняется нулю, т. е. они ортогональны.

Так как любое скалярное произведение двух различных столбцов в матрице X должно быть равно нулю, то это называется условием ортогональности матрицы X, а соответствующее планирование эксперимента (определение сочетаний факторов) называется ортогональным планированием.

Для ортогонального планирования при учете того, что ^хои ^ •••".

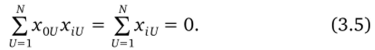
Таким образом, при ортогональном планировании сумма элементов любого столбца матрицы X, кроме первого столбца, должна быть равна нулю. Это правило используется при построении плана эксперимента, т. е. при определении того, каким образом нужно менять значения факторов в опытах. Это правило показывает, что в ортогональном планировании при четном числе уровней, на которых фиксируется каждый фактор, эти уровни должны быть симметрично расположены относительно центральной точки х = 0, при нечетном числе уровней должна использоваться и центральная точка (рис. 3.10).

Кроме свойства ортогональности план может обладать свойствами насыщенности, ротатабельности и др. План является насыщенным, если общее число опытов N равняется числу неизвестных коэффициентов полинома т + 1.

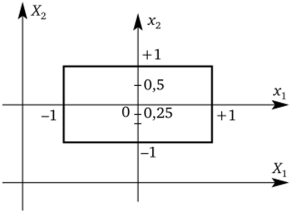
Рис. 3.10. Выбор уровней варьирования при ортогональном планировании.

План называется ротатабельным, если дисперсия отклика одинакова на одном расстоянии от центра плана при любом направлении в факторном пространстве. В упрощенном виде это означает, что все точки плана лежат на окружности (сфере, гиперсфере). Предположим, что функция отклика имеет вид Глава 3. Основы планирования эксперимента.

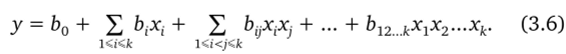
Используя ПФЭ типа 2^к, для функции отклика (3.6) могут быть получены МНК-оценки всех неизвестных коэффициентов Ь₀, {Ь,}, {Ьц}, …, b_{l2 к} [4]. В уравнении (3.6) число неизвестных коэффициентов р + 1 = 2*.

Множество всех точек в /с-мерном пространстве, координаты которых являются комбинациями «+» и «-» (соответственно верхний и нижний уровень фактора), называется полным факторным планом или планом ПФЭ типа 2^к. Количество точек в этом плане, очевидно, N = 2^к. При использовании неполных полиномов к-то порядка (3.6) количество точек плана равно количеству оцениваемых параметров (насыщенное планирование), поэтому не останется степеней свободы для проверки гипотезы адекватности представления результатов эксперимента заданной моделью. Если применять полиномы первой степени, то остаются степени свободы для проверки гипотезы адекватности модели.

Эффект взаимодействия вида лг, х.- называют парным, или взаимодействием 1-го порядка, x₍XjX_k — тройным, или взаимодействием 2-го порядка и т. д. Видно, что с ростом количества факторов число возможных взаимодействий быстро увеличивается. Уравнение (3.6) помимо свободного и линейных членов содержит все взаимодействия до (fc-l)-ro порядка включительно. Число взаимодействий (т — 1)-го порядка определяется по формуле.

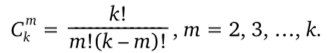
Именно поэтому в (3.6) число неизвестных коэффициентов p+l=N = 2^k= X С" .

т=0.

Матрица D_k+] полного факторного плана 2 может быть получена с помощью матрицы D_k плана 2^к по формуле.

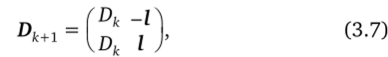
где I = (1, 1,…, 1)' — 2^{, с}-мерный вектор.

Для примера рассмотрим ПФЭ с тремя независимыми переменными (табл. 3.5).

Таблица 3.5. ПФЭ с тремя независимыми переменными.

Таким образом перебираются все возможные комбинации сочетаний факторов. Пятый — восьмой столбцы содержат значения произведений независимых переменных. Фиктивная переменная х₀ = 1 (первый столбец) введена для единообразия записи расчетных формул коэффициентов полинома. Строки соответствуют опытам, например, первая строка характеризует эксперимент, в котором все независимые переменные находятся на нижнем уровне. Видно, что спектр плана (точки наблюдения) находится в вершинах куба (см. рис. 3.4). Построение матрицы (3.7) основано на последовательном достраивании матрицы. Для этого при добавлении нового фактора необходимо повторить комбинации уровней исходного плана сначала при значении этого фактора на нижнем уровне, а затем на верхнем или можно воспользоваться правилом чередования знаков. В столбце х, знаки чередуются, во втором чередуются через 2, в третьем — через 4, в четвертом — через 8 и т. д. Из структуры матрицы (3.7) следует, что все ее 2^к+1 строк различные. Также столбцы матрицы плана D_fc+1 ортогональны. Из анализа матрицы независимых переменных X = (x_iu), (i = 0, 1,…, р, и = 1, 2,…, N) легко видеть, что полный факторный эксперимент обладает свойствами:

Как видно из табл. 3.5, матрица плана ПФЭ 2³ (второй, третий, четвертый столбцы).

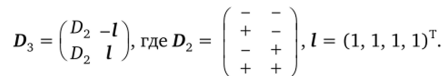
• ортогональности; сумма парных произведений элементов любых двух различных столбцов равна нулю:

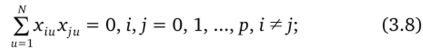
• симметричности; сумма всех элементов любого столбца, за исключением первого, равна нулю:

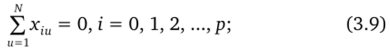
• нормированности; сумма квадратов элементов любого столбца равна числу опытов:

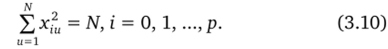
Первые два свойства обеспечивают независимость оценок коэффициентов модели и допустимость их физической интерпретации. Нарушение этих свойств приводит к взаимной зависимости оценок и невозможности придания смысла коэффициентам.

Так как планирование является ортогональным, то, полагая Ь_к+1 = Ь₁₂,…, Ь_р = Ь_{12 к}, оценки коэффициентов полинома вычисляются по простым соотношениям.

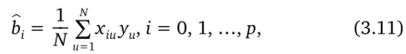
где у_и соответствует значению отклика в указанной точке факторного пространства при отсутствии повторных опытов.

Их дисперсии являются одинаковыми и равны.

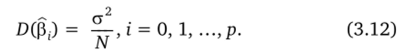
Дисперсии оценок всех коэффициентов определяются только дисперсией функции отклика и числом опытов.

Допустима следующая интерпретация оценок коэффициентов:

• • Ъ₀ соответствует значению функции отклика в центре проводимого эксперимента;
• • Ь, равен приращению функции при переходе значения фактора i с нулевого уровня на верхний (это вклад соответствующего фактора в значение функции);
• • Ь_р равен нелинейной части приращения функции при одновременном переходе факторов г и с нулевого уровня на верхний и т. п.

Таким образом, ПФЭ 2^к позволяет получить несмещенные оценки всех неизвестных коэффициентов модели (3.6). Оценки являются некоррелированными, а их дисперсии — одинаковыми. Пусть априори известно, что некоторые из коэффициентов равны нулю, в этом случае функция отклика (3.6) изменится. Новой функции отклика будет соответствовать новая матрица независимых переменных, которая получается из старой вычеркиванием некоторых столбцов. Поэтому планирование будет по-прежнему ортогональным, следовательно, для вычисления оценок ненулевых коэффициентов и их дисперсий можно использовать те же самые формулы. Заметим, что включение в матрицу планирования переменных вида xf приведет к появлению единичных столбцов, совпадающих друг с другом и со столбцом х₀. Следовательно, нельзя будет определить, за счет чего получено значение р₀. Поэтому планы ПФЭ 2^к неприменимы для построения функции отклика в виде полного полинома второй степени.