Обработка результатов дублированных опытов

Рассмотрим случай, когда проводятся повторные опыты (при одних и тех же значениях факторов), что на практике для компенсации влияния случайных погрешностей обычно имеет место. Обычно число п повторных опытов принимают равным 2-^3 или 4-^5. При исследованиях приходится иметь дело с тремя вариантами дублирования опытов в эксперименте: равномерное; неравномерное; без дублирования.

При равномерном дублировании все строки матрицы планирования имеют одинаковые числа параллельных опытов. В случае неравномерного дублирования числа параллельных опытов неодинаковы. Наиболее предпочтительным из трех вариантов дублирования является первый. При этом варианте эксперимент отличается повышенной точностью, а математическая обработка экспериментальных данных — простотой. Характер дублирования опытов влияет на содержание математической обработки результатов наблюдений.

Необходимым условием применения МНК для расчета оценок коэффициентов модели является однородность оценок дисперсии воспроизводимости среднего значения функции отклика во всех точках плана. Поэтому обязательным этапом обработки должна быть проверка статистической гипотезы об однородности совокупности дисперсий воспроизводимости. В зависимости от количества опытов в точках плана применяют критерии Кохрена, Фишера или Бартлетта.

Для каждой строки матрицы планирования по результатам п параллельных опытов вычисляется среднее арифметическое значение отклика.

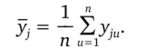
Опыт считается воспроизводимым, если дисперсия sf функции отклика в каждой точке факторного пространства однородна:

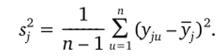
При равном числе повторов каждого эксперимента проверка однородности для дисперсии функции отклика осуществляется с помощью критерия Кохрена. Если отношение дисперсии функции отклика в точке факторного пространства, где она максимальна s^_ax, к сумме дисперсий во всех точках.

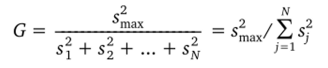
меньше критического, то дисперсия считается однородной. То есть при G < G_Kp опыты воспроизводимы, где G_Kp — критерий Кохрена уровня значимости, а и с числами степеней свободы п — 1 и N.

При разных количествах повторов каждого эксперимента проверка однородности дисперсии функции отклика осуществляется с помощью критериев Фишера или Бартлетта [5, 6]. Применение критерия Фишера сводится к проверке гипотезы о равенстве дисперсий двух нормально распределенных случайных величин. Из совокупности оценок дисперсии среднего значения функции отклика выбираются s^_in и s^_ax значения с числом степеней свободы соответственно.

min = n_min — 1 и Фшах = ^пшах- !• Вычисляется значение F = s²_jn/s^_ax, которое сравнивается с критическим значением F_Kp = F (a; (p_min; cp_max), где, а — уровень значимости.

Проверка однородности по критерию Бартлетта учитывает оценки дисперсии воспроизводимости во всех точках плана и производится на основе вычисления.

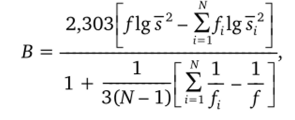
ГД efi = (п, — 1),/= ZftS² = j’Zsffi-

Случайная величина В при справедливости гипотезы об однородности дисперсий распределена приближенно как.

с N — I степенями свободы, если все п_{ > 3. Следовательно, В_кр = у²(а, N — 1). Если В < В_кр, то гипотеза об однородности принимается, в противном случае отвергается.

Если не выявлена неоднородность дисперсии воспроизводимости, то обработку результатов экспериментов можно продолжать дальше. В противном случае следует выявить и устранить причины неоднородности.

Все коэффициенты, их дисперсии, оценки дисперсии коэффициентов вычисляются по формулам.

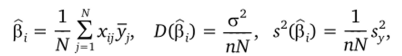
1 ^N

где s² = — Us? — несмещенная оценка дисперсии функции.

* N j= 1 ^;

отклика (дисперсия воспроизводимости). В случае различного дублирования опытов дисперсия воспроизводимости функции отклика определяется как.

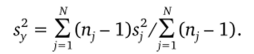
Значимость коэффициента определяется с помощью критерия Стьюдента. Если.

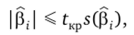
где t_Kp по выбранному уровню значимости а и числу степеней свободы N (n — 1) находится по таблицам, то коэффициент незначим.

После проверки значимости коэффициентов может оказаться, что все они незначимы. Эти выводы являются следствием того, что достигнута область оптимума функции отклика. Поэтому следует перейти к построению функции на основе полных полиномов второго порядка.

Необходимо добавить, что при равномерном дублировании опытов на практике можно использовать эквивалентную схему обработки результатов, учитывающую усреднение непосредственно.

1. Определяются коэффициенты регрессии.

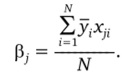
Матрица X в этом случае содержит только отличающиеся вектор-строки, а матрица Р = пЕ.

2. Находится дисперсия адекватности.

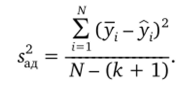
3. Оценивается дисперсия среднего по строкам.

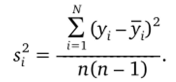
4. Проверяется гипотеза об однородности дисперсий и после ее принятия находится общая дисперсия среднего.

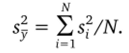
5. Вычисляется дисперсия оценок коэффициентов регрессии.

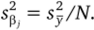
6. Проверяется гипотеза адекватности модели.

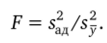
Пример 2.15.

Обработать результаты, представленные в табл. 2.18. Коэффициенты регрессии (3₀ = 1,46 25, pj = 0,4625, р₂ = 0,2875.

Таблица 2.18. Матрица планирования и результаты опытов

Дисперсия адекватности s², = 12,5 х юЛ Дисперсии среднего по строкам (см. табл. 2.18) s² = 0,02, 4 = 0,02, s² = 0,045, s² = 0. Критерий Кохрена G = 0,44, гипотеза об однородности дисперсий принимается. Общая дисперсия среднего = 0,106. Дисперсия оценок коэффициентов регрессии ^ = Sy/N = 0,106/4 = = 0,265. Проверка гипотезы адекватности модели F = 4дЛюс_Пр = — 0,5 896.

Пример 2.16.

Пусть реализован план с неравномерным дублированием опытов, в котором первый опыт дублирован дважды. Матрица X.

имеет вид.

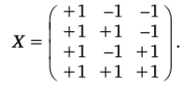
Решение системы нормальных уравнений с учетом весов.

Выполним указанные действия.

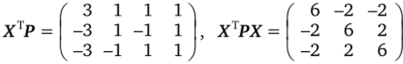
Дублирование одного опыта нарушило ортогональность плана. Применение стандартных формул для подсчета коэффициентов регрессии, используемых в случае ортогональных планов, стало неправомерным.

Найдем обратную матрицу.

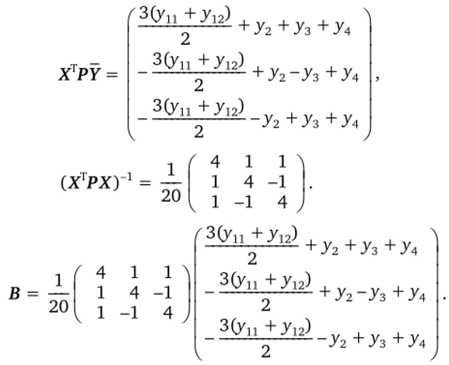
Заметим, что к тому же результату можно прийти, используя обычные формулы для нахождения оценок коэффициентов регрессии, например:

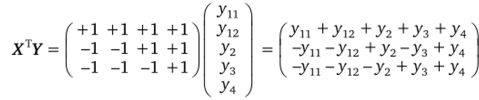
Пусть в ходе экспериментирования производилось дублирование точек в соответствии с матрицей X и получены результаты, изображаемые вектором Y.

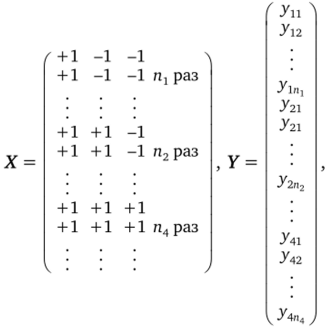
где n, — число параллельных (дублированных) опытов в первых условиях i = 1, 2, N [6]. Общее число всех опытов будет равно.

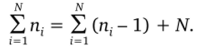
Перейдем к более лаконичной форме записи условий и результатов эксперимента. Для этого введем матрицу весов Р. Это квадратная диагональная матрица с элементами р_и = п₍.

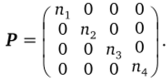
Она в совокупности с матрицей X, содержащей только неповторяющие строки, задает условия эксперимента, а его результаты тогда можно представить в виде вектора Y, состоящего из средних наблюдений по дублированным опытам. Для учета различных вариантов дублирования составим таблицу, в которой приведем формулы для разных случаев (табл. 2.19).

Таблица 2.19. Суммы квадратов и числа степеней свободы при дублировании опытов.

В табл. 2.19 также указаны формулы для случая, когда дисперсия, характеризующая ошибку опыта, находится из независимой серии опытов, результаты которой не используются при вычислении коэффициентов регрессии. Таким образом, неравномерность дублирования должна учитываться и при регрессионном, и при дисперсионном анализе.

Для рассмотрения частных случаев, возможных при различных стратегиях дублирования, выразим соответствующие суммы квадратов с помощью обычной формы записи. Запишем выражение для остаточной суммы квадратов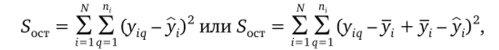

гдеу, — среднее значение отклика по опытам i-й серии. Раскрывая выражение для S_0CT, будем иметь.

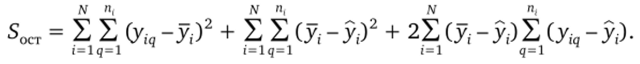
Сумма Z (у, —₀ -у,), входящая в последнее слагаемое, равна.

q=i.

нулю.

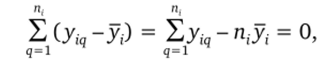
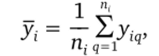
N л, JV.

поэтому S_0CT = X X (у, -у,)² + X п,(у, — у,)² дает разложение.

i=lq=1 i=l

на два слагаемых, первое из которых S_B0Cnp, а второе 5_ад.

С величиной S_0CT связано число степеней свободы, равное.

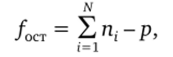
где р — число коэффициентов регрессии, входящих в регрессионную зависимость (в линейном случае р = к — 1). Величина.

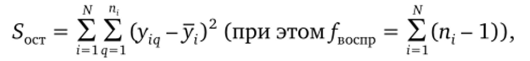
связана с числом степеней свободы. Следовательно, дисперсия.

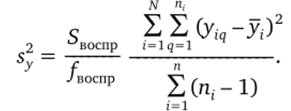
Тот же результат будет, если использовать выражения для частных дисперсий в каждой серии дублированных опытов [6]. Действительно, для i-й серии параллельных опытов можно записать.

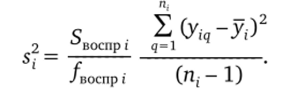
Тогда объединенная оценка дисперсии, характеризующей ошибку опыта, может быть найдена из соотношения.

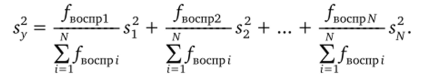
Применение этой формулы оправданно лишь при однородности частных дисперсий, которая может быть проверена в общем случае с помощью критерия Бартлетта. Запишем нашу формулу в виде.

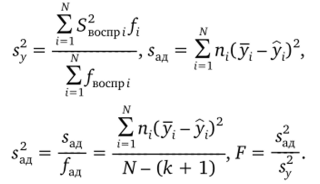
Она связана с числом степеней свободы /_ад = N — (к + 1) или в общем случае/^ = N-p.

Таким образом, содержащиеся в таблице формулы являются частными случаями одного и того же разложения остаточной суммы квадратов S_0CT. Наиболее общий случай представляет собой неравномерное дублирование. Чтобы получить здесь значение критерия, нужно сумму квадратов, связанную с дисперсией воспроизводимости, разделить на соответствующее ей число степеней свободы и получить знаменатель критерия (если построчные дисперсии однородны по критерию Бартлетта):

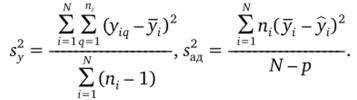
При дублировании в одной строке матрицы (в нашей таблице эта строка имеет индекс 1, хотя ясно, что выбор строк произволен) симметрия нарушается, это находит отражение в формулах. Из-за экономии времени приходится ставить параллельные опыты только в одной точке, и здесь лучше всего выбирать центр плана, ибо при этом не нарушается ортогональность.

Пример 2.17.

Составить регрессионную модель массового расхода расходомерной шайбы на основе статистических данных (табл. 2.20).

Массовый расход расходомерной шайбы (рис. 2.3) в основном зависит от геометрических параметров, используемых в конструкции. Ограничиваясь рассмотрением регулируемых расходомерных шайб с непрерывным контуром, можно принять, что определяющими факторами, существенно влияющими на массовый расход расходомерной шайбы, будут его геометрические параметры, а именно: максимальные и минимальные диаметры критического и выходного сечений D* и D_cp, а также длина сверхзвуковой фаски L.

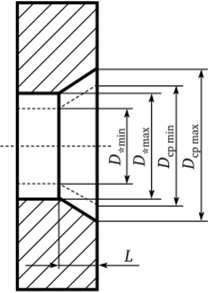
Рис. 2.3. Схема расходомерной шайбы с непрерывным контуром.

Зависимость массового расхода расходомерной шайбы от этих определяющих параметров находилась путем применения множественного регрессионного анализа к ряду известных конструкций расходомерных шайб.

В результате измерения массового расхода девяти различных расходомерных шайб и их основных геометрических параметров D*, D_cp и L были получены данные, которые после обезразмеривания были сведены в табл. 2.20.

Таблица 2.20. Результаты измерения массового расхода.

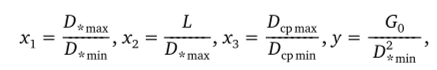
где G₀ — массовый расход.

Влияние основных безразмерных геометрических параметров массового расхода расходомерной шайбы аппроксимировали линейной зависимостью. Уравнение множественной регрессии было записано в виде.

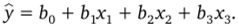
Далее были определены средние значения функций откликау и j-x независимых параметров Ц, а также среднеквадратичные отклонения функции отклика S_y и j-x независимых параметров S :

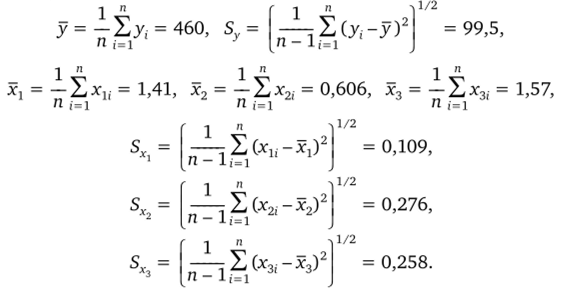
Далее была произведена нормировка всех величин по формулам (табл. 2.21):

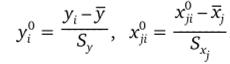
Таблица 2.21. Нормированные величины.

Уравнение регрессии было переписано:

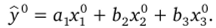
Затем были определены выборочные коэффициенты корреляции:

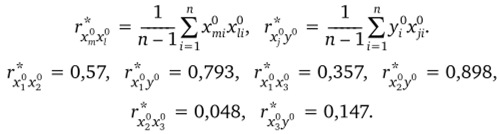
Анализ выборочных коэффициентов корреляции показал:

1. Существует тесная связь между диаметром критического сечения, длиной сверхзвуковой фаски и массовым расходом расходомерной шайбы (г*₀ о = 0,793 и г*_{0 0} = 0,898).

^хУ ^Х'У

2. Диаметр выходного сечения практически не влияет на массовый расход (г о «= 0,147).

^хз У

3. Существует тесная связь между величинами диаметров критического сечения и длинами сверхзвуковой фаски (г* ₀ = 0,57).

^{Х Х}2

В дальнейшем будем считать, что величина массового расхода определяется только диаметром критического сечения и длиной сверхзвуковой фаски, поскольку это значительно упростило регрессионный анализ.

Для определения значений а, и а₂ применялся МНК. Система нормальных уравнений имеет вид.

где X — матрица 9×2, составленная из значений нормированных факторов и х°, у⁰ — вектор нормированных значений у⁰ (см. табл. 2.21), а — вектор неизвестных параметров. После подстановки числовых значений (см. табл. 2.21) получили систему уравнений.

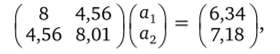
решив которую, нашли значения а^: dj = 0,416 и а₂ = 0,661. Переход к натуральному масштабу осуществлялся по формулам.

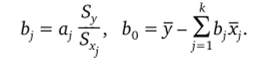
После определения коэффициентов Ь_} было составлено уравнение множественной регрессии.

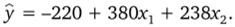
Далее производилась проверка адекватности полученного уравнения множественной регрессии по критерию Фишера.

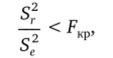
п М Е (у,-у,)² Е (у_г,-у,)²

где Sf = —-г—, S? = —.

п-к ^е М-1.

S² — остаточная дисперсия, характеризующая отклонение у, от у,-, определяемых из уравнения множественной регрессии;

S?—дисперсия воспроизводимости, определяемая из М реализаций^ (т.е. из М значений одной и той же расходомерной шайбы у_ф полученных в результате производственных отклонений при его изготовлении) при фиксированных значениях х, х₂,…, х_к;

F^ — критерий Фишера при /, = п- /си/₂ = М-1;

/_1;2 — число степеней свободы.

Дальше определялись S? и Sf: S? = 883 при/, = 7, а дисперсия воспроизводимости, например, для пятой расходомерной шайбы по трем реализациям у₅ S² = 68 при/₂⁵⁾ = 2, для девятой расходомерной шайбы по пяти реализацияму₉ S² = 331 при/₂⁽⁹⁾ = 4.

По таблицам [25] при уровне значимости, а = 0,05 были определены значения критерия Фишера: для пятой расходомерной шайбы при/, = 7 и/₂ = 2 — F_Kp = 19,36, а для девятой расходомерной шайбы при/, = 7 и/₂ = 4 — F^, = 6,09. Отношение остаточной дисперсии к дисперсии воспроизводимости для пятой расходомерной шайбы составило 12,94, а для девятой — 2,67, т. е. в обоих случаях отношение дисперсий меньше соответствующих значений критерия Фишера. Проверка по критерию Фишера позволила сделать вывод об адекватности полученного уравнения множественной регрессии при уровне значимости а = 0,05.

Затем определялись допустимые ошибки 5, определения у, по уравнению множественной регрессии.

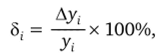
где Ду, — стандартная ошибка индивидуального предсказания:

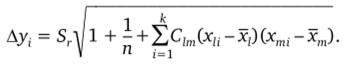
Величины C_im определялись, как показано в [34], решением систем к линейных уравнений, коэффициентами которых являются выборочные коэффициенты корреляции:

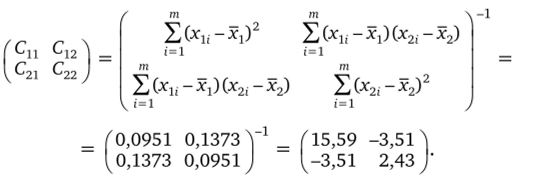
Уравнение стандартной ошибки индивидуального предсказания было получено в следующем виде:

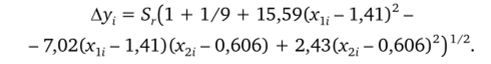
Результаты расчетов допустимой ошибки б, и величины у, для реальной ошибки.

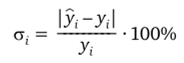
сведены в табл. 2.22.

Таблица 2.22. Значения реальной ошибки.

Как видно из табл. 2.22, только в одном случае (для первой расходомерной шайбы) ошибка определения массового расхода по уравнению множественной регрессии несколько больше допустимой. В среднем ошибка определения массового расхода расходомерной шайбы по уравнению регрессии а = 4,7% меньше средней допустимой ошибки б = 7,5%.

Проверим применимость уравнения множественной регрессии для расходомерных шайб, не входивших в рассмотренную ранее выборку. Для десятой расходомерной шайбы у = 529, х, = = 1,607 и х₂ = 0,7, а для одиннадцатойу = 562, Х] = 1,473 и х₂ = = 0,717. Величины у, определенные по уравнению множественной регрессии, равны соответственно 557 и 510. Величины допустимой ошибки — 12,8 и 9,8%. Величины реальной ошибки ст₁₀ = 5,3% и ст_п = 9,25% меньше соответствующих величин а₁₀

и ст_и. Таким образом, величины у ₁₀ иу_п находятся в пределах доверительного интервала, что свидетельствует о применимости уравнения (6) для десятой и одиннадцатой расходомерных шайб.

Пример 2.18

Выход у изделия из сборочного цеха зависит от двух факторов: времени t сборки узлов и динамического испытания под давлением Р. В окрестности точки t = 4 ч, Р = 220 кг/см² была построена линейная модель первого порядка, показавшая, что отклик растет пропорционально росту t и Р примерно с одинаковой скоростью. Для поиска максимального значения у было решено исследовать полимиальную модель 2-го порядка в окрестности точки f = 8 ч, Р = 260 кг/см², т. е. модель представляется полиномом второй степениу = (3₀ + р,*] + р₂х₂ + Р-,*² + р₄х₂ + Р 5*1*2;

В дальнейшем мы для упрощения вычислений введем норми;

«t — 8 Р — 260.

рованные переменные x_t их₂ (рис. 2.4), Xj = —у— , х₂ = —jy-;

кодированные переменные (рис. 2.5), при которых исходная точка (t = 8 ч, Р = 260 кг/см²) переходит в точку (х, = 0, х₂ = 0), а интервалы варьирования At = 1 ч, АР = 10 кг/см² переходят в Дх, = 1, Дх₂ = 1.

Было решено провести эксперимент в п = 9 различных точках, продублированы наблюдения в каждой точке дважды, т. е. I = 6, Vj = п -! = 3, v₂ = п (г — 1) = 9, где г = 2. Выберем 95%-ю надежность для t-критерия, а для F-критерия положим P (F > F_Kp).

— 0,99. При этом соответствующее значение F_Kp = 6,99. Результаты эксперимента и значения отклика, которые дает модель у =.

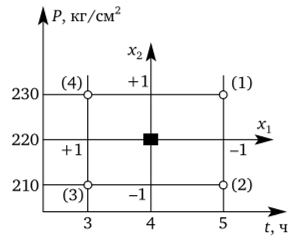
Рис. 2.4. Схема кодирования факторов.

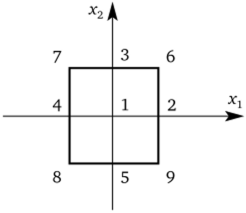
Рис. 2.5. Точки плана эксперимента.

= у (х), представлены в табл. 2.23. Линейная модель здесь уже оказывается недостаточной, так как целевая функция в окрестности оптимума имеет существенную кривизну. В каждой из указанных точек поставим по два эксперимента.

Таблица 2.23. Результаты наблюдений.

На основании данных табл. 2.23 находим вектор МНК-оценок. Согласно р = CF^lY и С = (F'F)" ¹, находим.

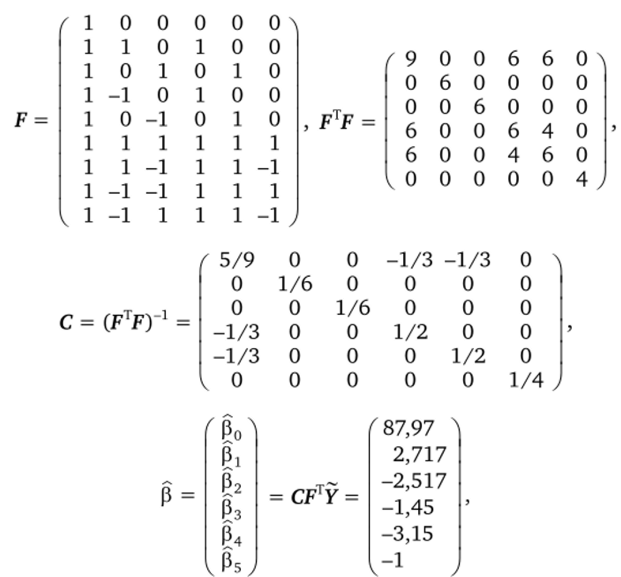
или.

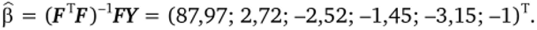
Тем самым модель (3.25) в кодированных переменных ху и х₂ найдена.

Проводя статистический анализ модели, находим вначале.

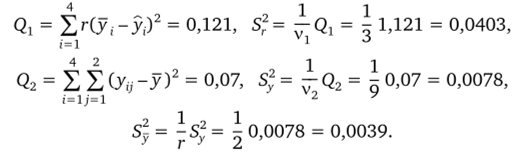
Проверяя адекватность модели (при а = 0,01).

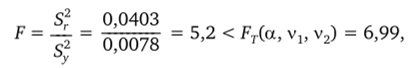
устанавливаем, что ее можно считать адекватной при заданном уровне значимости.

Проверяем значимости коэффициентов (при а = 0,01, t_Ta&,(«) = = 2,9):

следовательно, все коэффициенты значимы.

Доверительный интервал уровня у = 0,9 (z_y = 1,65) для у имеет вид.

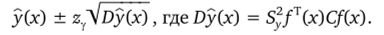
Для отыскания точки х*, в которой у (х*) = max, решаем систему уравнений (линейных)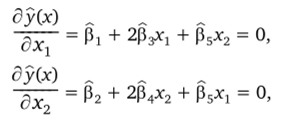

Возвращаясь к исходным переменным t и Р, находим точку экстремума.