Дедуктивные умозаключения с двумя посылками (простые силлогизмы)

Формально процесс вывода заключения строится так. Знак «о» выполняет функцию нуля, так обозначает нулевую вероятность существования обозначаемой им ветви дерева. Его умножение на любой другой знак снова дает «о». Значит, вероятности продолжения ветвей АВС и AB-iC равны нулю. По этой причине все ветви, отмеченные знаком «о», не имеют продолжений. Аналогичным образом и вероятность ветви A-iBCбыть… Читать ещё >
Дедуктивные умозаключения с двумя посылками (простые силлогизмы) (реферат, курсовая, диплом, контрольная)
Дедуктивные умозаключения вида:
Эта водоплавающая птица не крякает.
Все утки крякают.
Эта водоплавающая птица — не утка, в котором ровно две посылки, принято называть простыми силлогизмами (от греч. syllogismos — «сосчитывание», «выведение»). Посылки отделяются от заключения, как правило, горизонтальной чертой — графическим символом отношения логического следования (заключение записывается под чертой). Силлогизм в целом читается следующим образом: если истинны посылки «Эта водоплавающая птица не крякает» и «Все утки крякают», то с необходимостью истинно и заключение «Эта водоплавающая птица — не утка».
Создал теории силлогизмов Аристотель. Позже средневековые схоласты придали ей совершенный по тем временам вид учебной дисциплины, и с тех пор решение силлогизмов составляет важнейшую часть любого курса традиционной логики.
Формальное определение простого силлогизма таково:
Три суждения образуют простой силлогизм, если.
- 1) три различных термина силлогизма (Д Б и С), возможно, со знаками отрицания, есть независимые понятия с одним общим универсумом U
- 2) одна из посылок содержит субъект заключения (А) и исключаемый термин (Б), другая — предикат заключения © и исключаемый термин (Б);
- 3) исключаемый термин (Б) в заключении отсутствует;
- 4) все суждения связаны отношением логического следования так, что одно из них (заключение) выступает необходимым условием истинности двух других (посылок).
При решении силлогизмов существенное значение имеет выполнение пункта 1 из определения силлогизма, т. е. нахождение ближайшего общего универсума для всех трех терминов. Если его определить нельзя, силлогизм решения не имеет. Например, подавляющее большинство начинающих изучать логику пытается найти необходимое заключение из посылок следующего силлогизма Л. Кэрролла:
Сахар сладкий.
Все дети любят сладкое, т.
При этом не обращается внимание на то, что посылки не являются разновидностями (ближайшего) общего универсума. В первой говорится о продуктах, во второй — о людях. Напомним, что универсум понятия должен представлять объем ближайшего родового понятия; универсум суждения — ближайший класс вещей, обобщающий оба его термина; универсум простого силлогизма — ближайший класс вещей, обобщающий все три его термина.
Продолжим анализ силлогизма о птицах. Согласно приведенному выше определению, А обозначает субъект заключения, В — исключаемый (средний) термин, С — предикат заключения. Функция исключаемого термина В заключается в том, чтобы связать субъект и предикат заключения в одно смысловое целое в соответствии со следующей аксиомой силлогизма:
Из А следует Вниз В следует С.
Из А следует С. ().
Аксиома силлогизма гласит, что после того, как термины А и С связаны термином В} последний может быть исключен из дальнейшего анализа.
Порядок посылок в силлогизме несущественен, впрочем несущественно и то, каким термином — А или С — обозначается субъект заключения. Для любого силлогизма важно правильное определение исключаемого термина В. Чтобы это было корректным, необходимо найти понятие, входящее в обе посылки — возможно, со знаком отрицания или без него. Других таких понятий в силлогизме не должно быть.
В приведенном примере: А = «птицы, принадлежащие к классу „этих водоплавающих“», В = «птицы, которые крякают», С = «птицы, являющиеся утками», U = «птицы». В символической записи силлогизм выглядит следующим образом:
Ни одно А не есть В. Все С есть В.
Ни одно А не есть С.
Чтобы решать силлогизмы, надо знать соответствующие правила. Прежде чем их сформулировать, закончим анализ примера с птицами. Допустим, мы не знаем, что следует из посылок в качестве дедуктивного заключения. Как можно это выяснить, исходя только из информации, сообщаемой посылками?
Так как буква А обозначает субъект заключения, то ищем посылку, в которую она входит, и строим соответствующее ей дерево согласно табл. 3.1 (см. далее). Получаем:
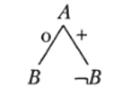
Отмечаем, что буква Л связана разрешающим знаком «+» с буквой -В. Значит, чтобы продолжить дерево, необходимо преобразовать оставшуюся посылку таким образом, чтобы на месте ее субъекта также появилась букваIВ. Только в этом случае будет выполнена аксиома силлогизма (*).
Вторая посылка имеет вид «Все С есть В». Значит, достаточно ее противопоставить, чтобы выполнить требование аксиомы (*). Результат противопоставления таков: «Все -В естьчС». Создаем дерево этой посылки и присоединяем его к уже построенному дереву первой посылки. В итоге получается:
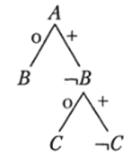
О чем свидетельствует полученное дерево силлогизма? Оно показывает, что все птицы, обладающие свойством Л, также обладают свойством -1 Я, а все птицы, обладающие свойствами А иуВ, обладают и свойствомпС. Отбрасывая в соответствии с требованием аксиомы силлогизма (*) промежуточный термин ->В, получаем, что все птицы, обладающие свойством А, необходимо обладают свойством ->С, т. е. выводится заключение «Все А есть -«С» или, после превращения, «Ни одно Л не есть С».
Формально процесс вывода заключения строится так. Знак «о» выполняет функцию нуля, так обозначает нулевую вероятность существования обозначаемой им ветви дерева. Его умножение на любой другой знак снова дает «о». Значит, вероятности продолжения ветвей АВС и AB-iC равны нулю. По этой причине все ветви, отмеченные знаком «о», не имеют продолжений. Аналогичным образом и вероятность ветви A-iBCбыть продолженной нулевая, так как умножение «+» на «о» дает «о». Поскольку сумма вероятностей для всех ветвей дерева всегда равна 1, то следует, что вероятность для ветви А-лВ-iC максимальна, т. е. составляет 1. В результате силлогистическое дерево принимает следующий вид:
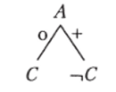
что и доказывает необходимость заключения «Все Л естьiС» или, что-то же, «Ни одно А не есть С».
Изменим первую посылку в нашем силлогизме:
Некоторые А не есть В.
Все С есть В.
Что следует?
Дерево первой посылки принимает следующий вид:
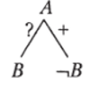
Дерево второй посылки остается без изменения. Объединив оба дерева в одно, получаем:
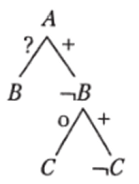
Как это можно понять? Знак неопределенности «?», которым отмечено суждение «Некоторые А есть Д», означает, что у нас нет однозначной информации о том, связан ли термин А с В знаком «+» или знаком «о». По этой причине нельзя исключить возможность связи А с В и С знаком «+». И поскольку такой альтернативы исключить нельзя, то независимо от знака «о», маркирующего суждение «НекоторыетВ есть С», необходимым может быть только заключение «Некоторые А не есть ?7».
Все заключения делятся на несколько видов согласно следующему определению.
Заключение
называется прямым, если оно начинается с А противоположным, если оно начинается с отрицания А, т. е. сЛ; обратным, если начинается с С; обратнопротивоположным, если оно начинается с отрицания С, т. е. с -.С.
Обратное заключение представляет результат обращения, противоположное — результат отрицания субъекта прямого заключения, обратно-противоположное — итог противопоставления прямого заключения.
Прямое, обратное, обратнопротнвоположное (или противоположное) заключения вместе исчерпывают все возможные виды решений силлогизма.
Правила решения силлогизмов можно разделить на правила построения силлогистического дерева (табл. 3.1) и правила вывода заключения (табл. 3.2).
Рассмотрим несколько примеров решения силлогизмов, посылки которых не интерпретированы в естественном языке.
Пример 1.
Доказать выводимость прямого заключения из следующих посылок:
Ни одно А не есть S.
Ни одно В не есть С.
Ни одно Л не есть С.
Таблица 3.1
Правила построения силлогистического дерева
1. | Если опыт или интуиция сразу не подсказывают решение силлогизма, последовательно строятся его деревья для вывода заключения произвольного вида и в любом порядке. |
2. | Дерево силлогизма считается законченным, если и только если при его построении использованы все посылки. |
3. | Дерево силлогизма строится из деревьев посылок согласно шаблонам рис. 3.2, с использованием формул превращения, обращения и противопоставления. Дерево частной посылки всегда выбирается в качестве вершины дерева силлогизма. |
4. | Продолжается только та ветвь, которая отмечена знаком «+». Ни одна из ветвей, отмеченных знаками «о» или «?», далее не используется. |
5. | Вершиной и конечными узлами силлогистического дерева могут быть только Л, -Л, С илилС (и никогда В или -$). |
Таблица 3.2 Правила вывода заключения
1. | Если в верхней и нижней частях силлогистического дерева — только знаки «+» и «о», то заключение может быть как общим, так и |
частным. | |
2. | Если в верхней части дерева — знаки «+» и «?», а в нижней — «+», «о», то заключение может быть только частным. |
3. | Ничего не следует из данной формы дерева силлогизма в качестве необходимого заключения, если: а) оно не может быть закончено из-за появления в верхней части двух знаков «?»; 6) в его нижней части имеется хотя бы один знак «?». |
4. | Силлогизм в целом не имеет решения, если и только если нет прямого, обратного и обратнопротивоположного (или противоположного) заключения. |
Доказательство:
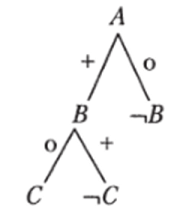
Доказать выводимость противоположного заключения из следующих посылок:
Все В есть -А.
Все С есть S.
Некоторые -А не есть С.
Доказательство (после обращения первой и противопоставления второй посылок):
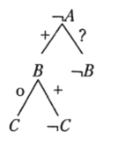
Пример 3.
Доказать выводимость обратного заключения из следующих посылок:
Все В есть -А.
Некоторые С не естьiВ.
Некоторые С не есть А.
Доказательство (после превращения второй посылки):
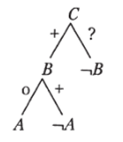
Пример 4
Доказать выводимость обратно-противоположного заключения из следующих посылок:
Ни одно А не есть В.
Ни один С не есть В.
Некоторые -, С не есть А.
Доказательство (после противопоставления и обращения второй посылки, обращения первой посылки):
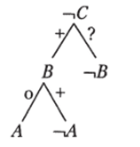
Пример 5.
Доказать, что следующий силлогизм не имеет решения:
Все А есть В.
Некоторые В есть С.
Доказательство. Невозможность прямого, обратного, противоположного, обратнопротивоположного заключений доказывают следующие деревья:
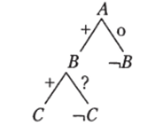
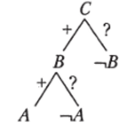
прямое заключение невозможно обратное заключение невозможно.
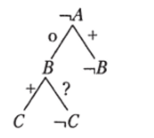
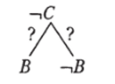
противоположное заключение обратнопротивоположное невозможно заключение невозможно Прямое, обратное и противоположное заключения не следуют с необходимостью из приведенных посылок, потому что в нижней части деревьев силлогизма стоят знаки «?». Обратнопротивоположное заключение не следует, потому что дерево силлогизма не было закончено из-за двух знаков «?», появившихся в верхней его части. Так как ни прямое, ни обратное, ни обратнопротивоположное (или противоположное) заключение из данных посылок невозможны, силлогизм в принципе не имеет дедуктивного решения. Это и требовалось доказать.
Допустим, посылки силлогизма сформулированы в естественном языке. В этом случае сначала приводим их к нормальной форме. Определяем универсум силлогизма и находим исключаемый термин. Следующий алгоритм позволяет быстро и надежно привести любой силлогизм к виду, удобному для формального решения.
Таблица 3.3
Алгоритм решения простого силлогизма.
|
делить ближайший общий универсум силлогизма, значит, данный силлогизм решения не имеет. |
3. Формализуем посылки. Ищем понятие, которое входит в обе посыл; |
ки в утвердительной и/или отрицательной форме. Если такое понятие есть и оно единственное, то это исключаемый термин. Обозначаем его буквой В. Если такого понятия нет или оно не единственное, то данный силлогизм решения не имеет. Рассматриваем первую посылку. То понятие, которое не является исключаемым термином, определяем как субъект заключения и обозначаем буквой А. Рассматриваем вторую посылку. То понятие, которое не является исключаемым термином, определяем как предикат заключения и обозначаем буквой С. |
|
ческого языка на естественный. |
Рассмотрим несколько примеров решения силлогизмов согласно указанному алгоритму.1
Пример 1.
Посылки Боль подтачивает силы человека.
Никакая боль не желательна.
Нормальная форма Все ощущения, называемые болью, есть посылок одцущения, подтачивающие силы человека.
Ни одно ощущение, называемое болью, не есть ощущение, которое желательно. Формализация посылок t/- «ощущения*, В — «болезненные*,.
А — «подтачивающие силы человека*,.
С — «желательные*.
1 Кэрролл Л. Логическая игра. — М., 1991. С. 57−62.
Все В есть А.
Ни одно В не есть С.
Дерево силлогизма А
А?
В
А.
С -iC.
Решение силлогизма Все В есть А.
Ни одно В не есть С.
Некоторые А не есть С.
Интерпретация Боль подтачивает силы человека.
силлогизма Никакая боль не желательна._.
Некоторые ощущения, которые подтачивают силы человека, нежелательны.
Пример 2.
Посылки Тем, кто лыс, расческа не нужна.
Ни одна ящерица не имеет волос.
Нормальная форма Ни одно лысое существо не есть существо,.
посылок которому нужна расческа.
Ни одно живое существо, являющееся ящерицей, не есть существо, имеющее волосы.
Формализация посылок U — «живое существо», В — «лысое»,.
А — «нуждающееся в расческе»,.
С — «являющееся ящерицей».
Ни одно В не есть А.
Ни одно С не есть S.
Дерево силлогизма А
°А+
В -.В
А*.
С с.
Решение силлогизма Ни одно В не есть А.
Ни одно С не есть -В.
Некоторые А не есть С.
Интерпретация Тем, кто лыс, расческа не нужна,.
силлогизма Ни одна ящерица не имеет волос.
Тот, кто нуждается в расческе, — не ящерица.
Посылки Все невнимательные люди совершают оплошности.
Ни один внимательный человек не забывает своих обещаний.
Нормальная форма Все невнимательные люди есть люди,.
посылок совершающие оплошности.
Ни один внимательный человек не есть человек, забывающий свои обещания.
Формализация посылок U — «люди», В — «внимательные»,.
А * «совершающие оплошности»,.
С — «забывающие свои обещания».
Все -1В есть А.
Ни одно В не есть С.
Дерево силлогизмаИ
А°.
В
«А*.
СпС
Решение силлогизма Все -чВ есть А.
Ни одно В не есть С.
Все —А есть -«С.
Интерпретация Все невнимательные люди совершают.
силлогизма оплошности.
Ни один внимательный человек не забывает своих обещаний._.
Тот, кто не совершает оплошностей, не забывает о своих обещаниях.
Пример 4.
Посылки Картошка — не ананас.
Все ананасы приятны на вкус.
Нормальная форма Ни один плод, называемый картошкой,.
посылок не есть плод, называемый ананасом.
Все плоды, называемые ананасами, есть плоды, приятные на вкус.
Формализация посылок U- «плоды», В = «называемые ананасами»,.
А — «называемые картошкой»,.
С — «приятные на вкус».
Ни одно А не есть В.
Все В есть С.
Дерево силлогизма С
Л?
ВлВ
А
АА
Решение силлогизма Ни одно А не есть В.
Все В есть С.
Некоторые С не есть А.
Интерпретация Картошка — не ананас,.
силлогизма Все ананасы приятны на вкус.
Существуют плоды, приятные на вкус и не являющиеся картошкой.
Пример 5.
Посылки Ни одна булавка не имеет честолюбивых намерений.
Ни одна иголка — не булавка.
Нормальная форма Ни одна вещь, называемая булавкой,.
посылок не является вещью с честолюбивыми намерениями.
Ни одна вещь, называемая иголкой, не является вещью, называемой булавкой.
Формализация посылок U — «вещи», В — «называемые булавками»,.
А — «имеющие честолюбивые намерения», С — «называемые иголками».
Ни одно В не есть А.
Ни одно С не есть В.
Дерево силлогизмаiС
*Л7
В -пВ.
А
А —А
Решение силлогизма Ни одно В не есть А.
Ни одно С не есть В.
Некоторые sC есть -А.
Интерпретация Ни одна булавка не имеет честолюбивых.
силлогизма намерений.
Ни одна иголка — не булавка.
Существуют вещи, не являющиеся иголками и не имеющие честолюбивых намерений.
Посылки Все разумные люди ходят на ногах.
Все неразумные люди ходят на руках. Нормальная форма Все разумные люди есть люди, посылок ходящие на ногах.
Все неразумные люди есть люди, ходящие на руках.
Формализация посылок U — «люди», В *" «разумные,.
А — «ходящие на ногах»,.
С — «ходящие на руках».
Все В есть А.
Все -1В есть С.
Дерево силлогизма С
А°.
В -, В л°.
АА
Решение силлогизма Все В есть А.
Все ->В есть С.
Все -.С есть А.
Интерпретация Все разумные люди есть люди, силлогизма ходящие на ногах.
Все неразумные люди есть люди, ходящие на руках.
Все, кто не ходит на руках, ходит на ногах.
Пример 7.
Посылки Занимайтесь своим делом.
Эта ссора — не ваше дело.
Нормальная форма Все ваши дела есть дела, которыми посылок немедленно следует заняться.
Ни одно дело, называемое «этой ссорой», — не есть ваше дело.
Формализация посылок {/- «дела», В — «ваши»,.
А ~ «которыми следует немедленно заняться», Сш «эта ссора».
Все В есть Л.
Ни одно С не есть В.
Дерево силлогизма А
л?
В -, В
А.
С -.с.
Решение силлогизма Все В есть А.
Ни одно С не есть В.
Некоторые А есть -*С.
Интерпретация Занимайтесь своим делом,.
силлогизма Эта ссора — не ваше дело.
Существуют дела, которыми следует немедленно заняться и которые не имеют отношения к этой ссоре.
Пример 8.
Посылки Некоторые сорта герани красного цвета.
Все эти цветы красные.
Нормальная форма Некоторые сорта герани — цветы красного.
посылок цвета.
Все эти цветы красного цвета.
Формализация посылок U = «цветы», В = «красного цвета»,.
А — «сорта герани», С" «эти».
Некоторые А есть В.
Все С есть В.
Дерево вывода А
прямого заключения
В -, В
л?
С —1С
Дерево вывода С
обратного заключения
В ~^В
А7
-А А
Дерево вывода противо- -А
положного заключения /^?
В -, В
Нет решения Некоторые А есть В.
Все С есть В._
Интерпретация Некоторые сорта герани есть цветы
силлогизма красного цвета.
Все эти цветы красного цвета.