Спор Протагора с Еватлом

Содержание спора сводится к следующему. У известного софиста Протагора (V в. до н. э.) был ученик Еватл, обучавшийся праву. По заключенному между учителем и учеником договору Еватл должен был заплатить за обучение лишь в том случае, если он выиграет свой первый процесс. Но, закончив обучение, Еватл не стал участвовать в йроцессах. Когда терпение Протагора иссякло, он подал на своего ученика в суд. Таким образом, Еватл столкнулся с необходимостью вступить в свой первый процесс.

Свой иск Протагор аргументировал следующим образом. Каким бы ни было решение суда, Еватл будет обязан заплатить за обучение. Ибо он либо выиграет, либо проиграет процесс; если выиграет, то заплатит в силу договора; если проиграет, то заплатит согласно решению суда.

Ответ Еватла был не менее аргументированным. Действительно, он либо выиграет, либо проиграет процесс. Если выиграет, то не обязан платить по решению суда; если проиграет, то не должен платить в силу договора.

Парадокс данного спора состоит в том, что при любом исходе судебного процесса Протагор и Еватл имеют равные логические основания требовать удовлетворения своих взаимоисключающих намерений (рис. 10.1). Причина парадокса также очевидна. Исходы любого решения, принятого судом, не будут несовместимыми и, следовательно, могут быть одновременно истинными. Именно о такой возможности и свидетельствуют аргументы обоих участников спора. Это означает,.

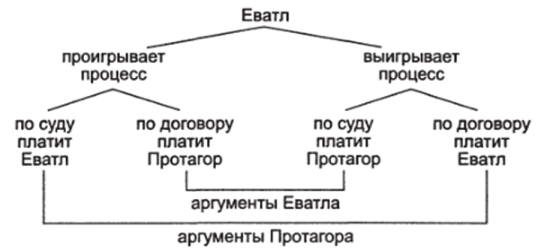
Рис. 10.1. Парадоксальная классификация исходов в споре Еватла с Протагором.

что классификация результатов судебного процесса проведена с нарушением по двум основаниям — «платить по решению суда» и «платить по договору» одновременно.

Для устранения парадокса необходимо признать оба условия независимыми и классификацию выполнить последовательно. Непарадоксальная структура спора имеет другой вид (рис. 10.2).

Цифры «О» и «1» на рис. 10.2 обозначают вероятности соответствующих исходов. Те из них, которые отмечены цифрой «0», неосуществимы по условиям сиора. Исходы, отмеченные цифрой «1», но условиям спора обязательно реализуются.

После правильного разбиения спор Протагора с Еватлом имеет только два возможных исхода.

• 1. Если Еватл проигрывает процесс, то он платит Протагору по суду и не платит по договору.
• 2. Если Еватл выигрывает процесс, то он не платит Протагору по суду, но платит по договору.

Рис. 10.2. Непарадоксальная классификация исходов спора Еватла с Протагором

Как интерпретировать указанные исходы? Есть три возможности интерпретации. Во-первых, можно считать, что независимо от решения суда Протагор выигрывает спор: Еватл, проиграв дело, заплатит ему за обучение по суду, а, выиграв, — по договору. Однако это неверно, потому что при этом не учитывается эффект компенсации платежных действий, составляющих одну и ту же альтернативу. Во-вторых, если принять последнее замечание к сведению, можно считать, что эффект компенсации платежей по суду и по договору ведет к общему нулевому исходу независимо от решения суда. Однако и эта возможность неверна, потому что упускается из виду начальное состояние спора: Еватл — должник Протагора, а не наоборот. Учет этого фактора рождает третью возможность, которую необходимо исследовать более подробно.

Пусть Уобозначает стоимость обучения Еватла у Протагора. По условиям спора Еватл прошел курс обучения, но не заплатил за него. Следовательно, приобрел У единиц стоимости, а Протагор потерял У единиц стоимости или, равно, приобрелУ единиц стоимости.

Рассмотрим первую альтернативу: Еватл платит за обучение по суду и не платит по договору. Отметим, что освобождение Еватла от платы за обучение по суду или по договору равносильно внесению ее самим Протагором в форме соответствующих издержек, которые были в процессе обучения. Согласно данной альтернативе будет следующая цепочка платежей: Еватл — владелец У единиц стоимости по условию спора; Еватл платит Протагору Уединиц стоимости посуду: У — У — 0; Еватл освобождается от уплаты обучения по договору: 0 + У = У. Общий исход спора для него в данном случае положительный: он сохраняет начальные У единиц стоимости, т. е. не платит Протагору за свое обучение и таким образом выигрывает спор.

Эта же альтернатива с точки зрения Протагора выглядит следующим образом. Протагор — владелецУединиц стоимости по условию спора; Еватл платит Протагору по суду за обучение У единиц стоимости: -У + У — 0; он освобождается от платы за обучение по договору, т. е. платит Протагор: 0 — У — - У. Общий исход для Протагора, согласно данной альтернативе, отрицательный: он не получает платы за обучение от Еватла, не возмещает своих издержек и тем самым проигрывает спор.

Рассмотрим теперь вторую альтернативу: Еватл не платит по суду, но платит за обучение по договору. С точки зрения Еватла, имеет место следующая цепочка платежей: Еватл — владелец У единиц стоимости по условиям спора; он освобождается от платы за обучение по суду:

V — 0 = V] платит Протагору за обучение по договору: V — V = 0. Общий исход для Еватла, согласно данной альтернативе, отрицательный: он вынужден заплатить Протагору за свое обучение и таким образом проиграть спор.

С точки зрения Протагора, возникает следующая цепочка платежей: Протагор — владелец — Vединиц стоимости по условиям спора; Еватл освобождается от платы за обучение по суду: -V + 0 = - V — и платит за обучение по договору: — V + V = 0. Общий исход спора для Протагора, согласно данной альтернативе, положительный: он получает от Еватла плату за обучение, покрывает свои издержки и таким образом выигрывает спор.

Для большей ясности варианты всех платежей сведены в таблицу.

Таблица 10.1

Суммарные платежи Еватла и Протагора

В условиях спора не содержится никакой информации о шансах на победу его участников. В этой ситуации разумно допустить, что как Протагор, так и Еватл имеют равные шансы на выигрыш.

Другими словами, победа любого из них представляет случайное событие. В этом состоит логическое содержание рассматриваемого спора, которое, как очевидно, не исчерпывает всей проблемы. Чтобы увидеть это, расширим рамки нашего анализа и допустим, что Протагор еще только раздумывает, подавать ему в суд на Еватла или нет.

В этой ситуации возникают следующие возможности. Протагор либо подает в суд на Еватла, либо не подает. Если не подает, то теряет не только Vединиц стоимости, но и определенную часть своей репутации как учителя. Обозначим этот исход как С,. Если он подает в суд на Еватла, то, как уже установлено, с равной вероятностью может выиграть или проиграть судебный процесс. Обозначим этот сложный исход, включающий две возможности, как С₂. Если Протагор выигрывает, он не только компенсирует V единиц стоимости, но и подтверждает свой авторитет как учителя. Обозначим этот исход как С₁₂. Если Протагор проигрывает процесс, то он не только теряет V единиц стоимости, но и подрывает свою репутацию как учителя. Обозначим этот исход как С₂₂. Очевидно, что полезность исходов C_v С₂₁ и С₂₂ для Протагора неодинакова. Отобразим полезности указанных исходов на шкалу от 0 до 1 таким образом, что u (C,_Jt) = 1, и (С_п) = 0. Остается вычислить полезность исхода С,. Допуская, что значение полезности С, находится между 0 и 1, получаем следующее упорядочение: и (С_2|) > м (С,) < и{С_п). Подставляя числовые значения, получаем: 1 < ы (С,) < 0, откуда следует, что u (C_t) = х (х — некоторое значение вероятности). Итак, значение полезности того, что Протагор не подаст в суд на Еватла, равно субъективной вероятности этого исхода.

Построим дерево решения с точки зрения Протагора. Пусть Л, = подавать в суд на Еватла, А₂ — не подавать в суд на Еватла. Дерево решения имеет следующий вид:

Здесь значение х находится в интервале (0,1), исходы С₂₁ и С₂₂ равновероятны ввиду случайного выигрыша участников спора. Приведенное дерево упрощается до:

Из анализа последнего следует: чтобы Протагор предпочел Л, альтернативе Л₂, т. е. подал в суд на Еватла, субъективная вероятность последней должна быть меньше 0,5. Можно с большой уверенностью предположить, что одних только соображений престижа будет достаточно Протагору, чтобы приписать Л₂ вероятность, меньшую 0,5. Иными словами, весьма вероятно, что даже при равных с Еватлом шансах выиграть Протагор обязательно подаст на него в суд.