Модальная силлогистика. 
Логика

Модальный шестнадцатиугольник Назовем суждение, начинающееся с оператора 0, проблематическим; начинающееся с оператора? — аподиктическим; без модального оператора — ассерторическим. Кроме суждений этих трех видов бывают и иные. Они будут указаны ниже.

Общеприняты следующие обозначения ассерторических суждений:

• • А — общеутвердительного «Все 5есть Р»,
• • I — частноутвердительного «Некоторые 5 есть Р»,
• • Е — общеотрицательного «Ни одно S не есть Р»,
• • О — частноотрицательного «Некоторые 5 не есть Р».

Тогда символы <�М, ОI, О Е, О О будут обозначать соответствующие виды проблематических суждений, a Q4, ?/, QЕ, ПО — аподиктических суждений.

Существует четыре вида простых суждений. Каждое из них может быть ассерторическим, проблематическим или аподиктическим. Значит, для объяснения отношений противоречия, противоположности, несовместимости без противоречия и противоположности, подчинения, независимости и частичной совместимости всех видов модальных суждений требуется построить 12-угольную фигуру. Но для объяснения базисных допущений модальной силлогистики потребуются еще четыре вершины. В итоге для исчерпывающего объяснения необходим модальный 16-угольник.

Укажем, какие виды модальных суждений находятся в отношении противоречия:

Разделим универсум простых модальных суждений согласно указанным отношениям противоречия на несовместимые и совместно исчерпывающие его классы, т. е. построим классификацию этих суждений (рис. 9.1). Универсум равен сумме 10 классов. Объем любого модального суждения равен сумме тех классов, в которые входит его знак (сумма оставшихся классов указывает логическое содержание данного суждения). Для простоты анализа указываются только объемы суждений.

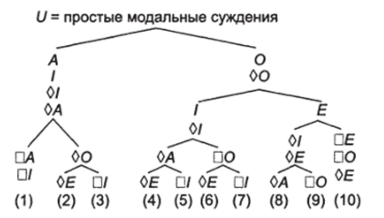
Рис. 9.1. Классификация простых модальных суждений Объемы простых модальных суждений.

А «(1+2 + 3)

/"(1 + 2 + 3 + 4 + 5 + 6 + 7)

• ?-(8 + 9+10)
• 0^е (4+ 5 + 6 +7+8 + 9 + 10)
• 0 А = (1 + 2 + 3 + 4 + 5 + 8)
• 01 =(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9)
• 0?= (2+ 4+ 6 + 8 + 9+ 10)

ОО = (2 + 3 + 4 + 5 + 6 + 7 + 8 + 9+10).

Q4 = (l).

• ?/=(1 +3 + 5 + 7)
• ??=(10)
• ?О = (6 + 7+ 9+ 10)

Знание объемов модальных суждений позволяет быстро убедиться в логической истинности следующих подчинений (следований):

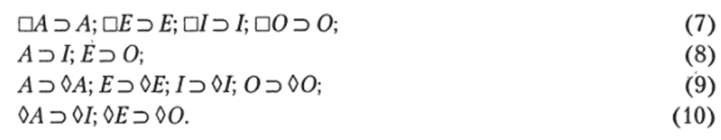
Понятие возможности, которое использовалось выше (см. первый параграф этой главы), назовем возможностью, совместимой с необходимостью. Ее особенность состоит в том, что она подчиняется как необходимости, так и действительности (см. формулы 7 и 9).

Существует также возможность, несовместимая с необходимостью. Она делится на две разновидности: Согласно первой одновременно возможны оба противоречащих друг другу суждения; согласно второй — одновременно возможны оба противоположных или оба частично совместимых суждения.

Первую разновидность возможности, несовместимую с необходимостью, обычно определяют как случайность. Мы назовем ее возможностью, совместимой с противоречием, или контрадикторной случайностью. Пусть ее символизирует знак т. Справедливо следующее определение (ф— произвольное суждение):

? ф, а (0ф & Оч0) (суждение 0 контрадикторно случайно, если и только если возможно как 0, так и противоречащее ему суждение -«0).

Согласно приведенному определению, контрадикторно случайность ф означает не необходимость его истинности и не необходимость его ложности.

Очевидно, что контрадикторно случайные суждения эквивалентны своим контрадикторно случайным логическим отрицаниям:

Сравнение объемов контрадикторно случайно возможных суждений и возможных суждений, совместимых с необходимостью, показывает, что между ними действуют следующие односторонние подчинения:

Подчинения (13)ч*(18) доказывают, что возможность, несовместимая с необходимостью, логически сильнее, чем возможность, совместимая с необходимостью. Все, что выполняется для суждений, начинающихся со знака т, также истинно для эквивалентных или подчиненных суждений, начинающихся со знака 0. Они также доказывают: все, что не выполняется для суждений, начинающихся со знака 0, ложно для эквивалентных или подчиняющих суждений, начинающихся со знака ?.

Возможность, несовместимая с необходимостью во втором смысле, не имеет специального названия. Назовем ее возможностью, совместимой с противоположностью, или контрарной случайностью (общих и частных суждений). Пусть ее символизирует знак ^А. Справедливо следующее определение:

*0 з (00 & 0ф*) (общее (частное) суждение ф контрарно случайно, если и только если возможно как ф, так и противоположное ему общее (частично совместимое частное) суждение — ф*).

Объемы контрарно случайных суждений, базисные следования и эквивалентности указаны ниже:

Согласно определению, общие контрарно случайные суждения исключают из универсума любые — общие и частные — суждения, перед которыми стоит знак необходимости Q Иными словами, дополнением общих контрарно случайных суждений служит дизъюнкция (СИЛ v ?? v ?/ v DO). Дополнением частных контрарно случайных суждений выступает дизъюнкция (CL4 v ОБ). Для сравнения укажем, что дополнением контрадикторно случайных суждений, что явствует из определения (11), будет дизъюнкция (Q4 v ?? v DO), а согласно определению (12) — дизъюнкция (ПА v ПЕ v ?/). Значит, контрарная случайность общих суждений более строгая, нежели контрадикторная. Напротив, контрарная случайность частных суждений логически слабее контрадикторной случайности. Так как общие контрарно случайные суждения исключают из универсума любые виды необходимых суждений, такую случайность можно приравнять к абсолютной.

Абсолютная случайность логически сильнее всех остальных видов случайности, а значит — и возможности, совместимой с необходимостью. Все, что выполняется для общих суждений, начинающихся со знака с необходимостью выполняется для эквивалентных или подчиненных им, в начале которых стоят 0,? или а. Все, что не выполняется для суждений, начинающихся со знака 0,? или, а для частных суждений, не выполняется для общих суждений, начинающихся со знака а. Исключение составляют следующие два подчинения для частных суждений:

Подчинения (25) и (26) свидетельствуют, что частные контрадикторно случайные суждения логически сильнее, чем частные контрарно случайные суждения.

Обращение модальных суждений, начинающихся со знака ?, совпадает с законами обращения ассерторических суждений (см. гл. 2). Для остальных модальных знаков ситуация обращения более неопределенная.

Пусть АаЬ обозначает общеутвердительное суждение с субъектом а и предикатом b lab, Eab, ОаЬ — частноутвердительное, общеотрицательное и частноотри цате л ыюе суждения с этими же терминами соответственно.

Тогда истинны следующие подчинения с обращением:

Доказательства формул (27)+(42) элементарны и они предоставляются читателю. Их результаты в обобщенной форме можно свести к следующим утверждениям.

• (А) Независимо от модального знака общеутвердительные суждения обратимы только в частноутвердительные соответствующей модальности.
• (I) Независимо от модального знака частноутвердительные суждения обратимы в частноутвердительные соответствующей модальности.
• (Е) Общеотринательные суждения с модальным знаком 0 или т обратимы в общеотрицательные суждения соответствующей модальности, но суждения с модальным знаком * необратимы в суждения данной модальности.
• (О) Частноотрицательные суждения с модальными знаками 0, т не обратимы, но с модальным знаком ^А обратимы в суждения этой же модальности.

Всю информацию о логических отношениях между модальными и ассерторическими суждениями содержит следующий 16-угольник — геккайдекаэдр (рис. 9.2; стрелками указаны отношения подчинения).

Не все отношения (всего их 120) между суждениями модального 16-угольника представлены графически. Остались неотображенными отношения несовместимости и независимости. Знание объемов модальных суждений, определений модальных знаков и подчинений позволяет легко восполнить данный пробел.