Определение радиуса сходимости

Отправляясь от коэффициентов степенного ряда (14), образуем последовательность чисел:

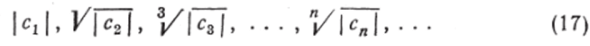
Бее члены этой последовательности рассматриваются как действительные неотрицательные числа.

Обозначим через / наибольший предел последовательности чисел (17) i = m^r[/c_n. Тогда радиус сходимости R степенного ряда (14).

л-к".

определяется по формуле:

t

Эта формула носит название формулы Коши-Адамара (Cauchy-Hadamard).

Замечание. В случае / = 0 в формуле (18) нужно положить /? = -|-ос, в случае / = +°° необходимо принять R = 0.

При выводе формулы (18) мы рассмотрим отдельно три случая:

• 1) / = +оо («= 0),
• 2) 1 = 0 (/? = +»),
• 3) 0</<+~ (Я=у).

В случае 1) (/ = + оо) последовательность чисел (17) неограниченная. Нам нужно доказать, что степенной ряд (14) расходится во всякой точке z> отличной от нулевой точки. Допуская противное, предположим, что ряд (14) сходится в некоторой точке г₀фО. Тогда имеем lim c_/xzj = 0 (гл. 1, § 5, п. 2); следовательно, существует по;

п-*эо '.

стоянное положительное число g такое, что выполняется неравенство ^СА<8 (^/г==0" 1″ 2,.. .). Мы можем предполагать число g ббльшим единицы. Из последнего неравенства, путём извлечения из обеих ого частей корня п-Й степени, следует: ^л/КН*о<�Уё, или.

УЫ<�Г —т, так как^п^ g 1). Таким образом, последовало I.

тельность чисел (17) оказывается ограниченной. Полученное противоречие убеждает нас в расходимости ряда (14) при любом z ф 0.

В случае 2) (/ = 0) нам нужно показать, что ряд (14) сходится в любой точке z = z₀. Так как последовательность чисел (17) сходится к нулю, то, начиная с достаточно большого п_} имеем:

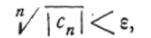
•например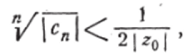

откуда.

«ли, по возведении в степень п:

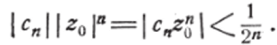
Так как ряд с общим членом ~ сходится, то абсолютно сходится и ряд с общим членом c_nzjj.

Если, наконец, / есть конечное число, отличное от нуля, то доказательство формулы (18) сводится к следующему: ряд (14) абсолютно СХОДИГСЯ при любом Z = z_l9 ДЛЯ которого |^i|^и расходится.

4ля каждого г = г_ъ для которого | ^гг₂1 •.

Так как / есть наибольший предел последовательности чисел (17), то имеем, начиная с достаточно большого п:

где s — сколь угодно малое положительное число. Заметив, что 7|^i|<^l, положим? = ~~2 г ** ' * Неравенство (19) примет вид.

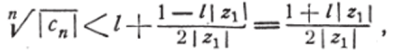
или.

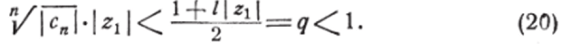
Возводя обе части неравенства (20) в степень л, найдём:

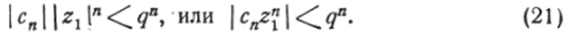
Так как ряд с общим членом qⁿ> q<^ 1 сходится, то в силу (21) абсолютно сходится данный степенной ряд при г = г_х.

С другой стороны, из определения / как предельного числа последовательности чисел (17) следует, что при бесконечно многих значениях п имеем:

где? — сколь угодно малое положительное число.

Заметив, что /|z₂|^>l, положим? = —. Неравенство (22).

I ^zt I.

перепишется так:

что по возведении в степень п даёт:

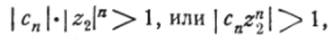
Так как последнее неравенство имеет место для бесконечного множества значений л, то c_nz% не может стремиться к нулю при неограниченном возрастании п. Отсюда следует расходимость данного ряда (14) при z = z₂ (гл. I, § 5, п. 2).

Примеры

• 1. Радиус сходимостт ряда 1 —z + z* + z* -f… равен единице. В самом деле, здесь с*= 1, если п — квадратное число, и равно нулю в прогивном случае. Таким образом, ^/с_п = 1 или 0, смотря по тому, имеем ли мы первый или второй случай. Предельные числа последовательности (17) будут О и 1. Следовательно, / = 1 и R =.
• 2. Радиус сходимости ряда

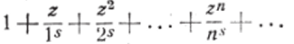
равен единице. Действительно,.

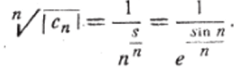
Так как стремится к нулю при п-+ оо, то ^п^с_п стремится к едиинице.

Следовательно, / = 1 и R=. 1.

3. Ряд.

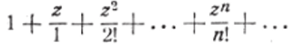
сходится во всей плоскости комплексного переменного г. Действительно, (л1)*=(1‘Л)[2(л —1)].. (л-1). Каждая скобка правой части последнего равенства не меньше л, так как имеем:

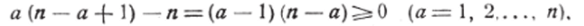
Следовательно, получаем (л!)' > п^п, или *!><�К п)^п, далее //! > |. п, г. е.

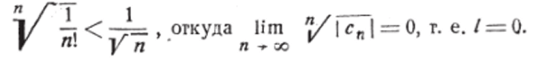
Следовательно, R= оо.

4. Аналогичным образом можно показать, что ряды.

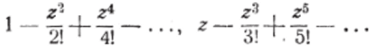
сходятся во всей плоскости комплексного переменного г, а ряд 1−4-г-р ~f-2!z² +… +л!г^я+ … сходится лишь в нулевой точке (/??=()).

Мы указывали, что на окружности круга сходимости степенной ряд может вести себя различно в разных случаях. Так, взяв пример 2 при 5=0, 1 и 2, получаем три ряда, для которых /?=1:

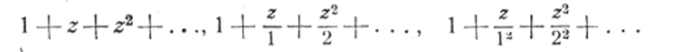
Первый р д расходится во всех точках окружности | z | = 1; последний сходится во всех точках этой окружности, а второй ряд сходится в одних точках этой окружности (например, при — 1) и расходится В других (при.

!) Можно было бы показать, что этот ряд расходится лишь при * = 1, в остальных же точках окружности 1*1—1 сходится.

Исследованию вопроса о сходимости степенного ряда на окружности его круга сходимости посвящены многочисленные работы, в которых даётся освещение этой проблемы с различных точек зрения.