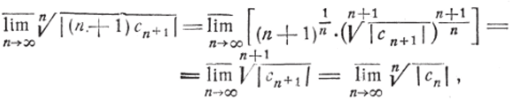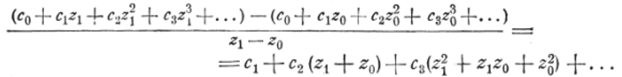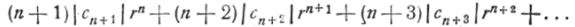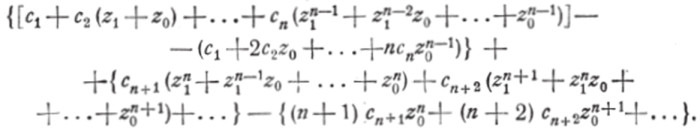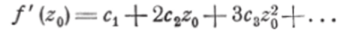Дифференцирование степенных рядов

Как мы уже указывали, всякий многочлен является аналитической функцией во всей плоскости комплексного переменного. Покажем теперь, что всякий степенной ряд, по отношению к которому многочлен является лишь весьма частным случаем, представляет собой аналитическую функцию внутри круга сходимости, причём производная от этой функции может быть получена путём почленного дифференцирования степенного ряда. Заметим сначала, что ряд <�р (z) = с_х -j- 2c₂z ?+ Sc^z² -f-. •., полученный почленным дифференцированием данного ряда: f (z) = c₀—c_xz + CnZ* + -f- • • • i имеет тот же круг сходимости, что и данный ряд. В самом деле.

откуда по формуле Коши-Адамара следует, что радиусы сходимости обоих рядов одинаковы. Пусть теперь z₀ — произвольная то 'ка внутри круга сходимости. Опишем внутри того же круга окружность z = r так,' чтобы точка z₀ лежала внутри неё, и пусть z_x — какая-либо другая точка, лежащая внутри этой окружности. Выражение.

²i — ²о

можно представить в виде:

Выбирая число п настолько большим, чтобы сумма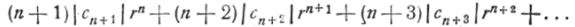

была меньше 4*" представим —.

₀) ^{в виде:}

о Z Zft

Первая из фигурных скобок стремится к нулю, когда z_x-+z_v и поэтому может быть сделана по модулю меньшей, если только.

z_x лежит в достаточно малой окрестности точки z₀. Чтобы оценить модуль второй скобки, перейдём к модулям отдельных слагаемых и заменим z_{ и z₀ ббльижм числом г. Получим тогда, что этот модуль меньше, чем (л+1) | с_п+_х |г^я-|-(л+^) I ^с_я+21 /" ⁺¹ +…, т. е. меньше, чем Точно так же, переходя от модуля суммы к сумме модулей.

«3.

и заменяя z₀ ббльшим числом г, получим, что модуль третьей фигурной скобки также меньше, чем 4*- Итак, ~~ —.

<^е, если z_x находится в достаточно малой окрестности точки z₀,.

откуда следует, что lim H^z^~~f (^z^ существует и равен <$(z₀), т. е. *г+*о ^Zl ~~ ^zo