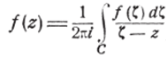Существование производных всех порядков для функции, аналитической в области

С помощью результатов предыдущего пункта мы можем доказать важное свойство аналитических функций. До сих пор мы называли однозначную функцию комплексного переменного z аналитической в области, если она имеет в каждой точке этой области конечную производную. В случае функции действительного переменного из факта существования конечной производной не следует непрерывности этой производной. В случае же функции комплексною переменного имеет место исключительно важное предложение: если однозначная функция f{z) комплексного переменного z имеет всюду в области G первую производную, то она имеет в этой области и производные всех высших порядков.

Замечание. Очевидно, эта теорема утверждает не только существование производных любого порядка для функции, аналитической в области G, но и непрерывность этих производных.

Доказательство. Пусть z есть производная точка области G и С—правильный замкнутый контур, окружающий точку z> лежащий вместе со всеми своими внутренними точками в области G. Применяя формулу Коши (п. 1), имеем:

С другой стороны, на основании предыдущего пункта функция fiz), изображаемая интегралом Коши, дифференцируема в точке z произвольное число раз. Следовательно, функция f (z) имеет производные всех порядков повсюду в области G, так как точка z была взята произвольно в области О.

в слу;

Наряду с основной формулой Коши (п. 2) имеет место — чае приложимости этой формулы — следующее равенство:

Итак, мы видим, что требование дифференцируемости функции комплексного переменного гораздо более сильное, нежели соответствующее требование для функции действительного переменного: из существования конечной производной первого порядка в каждой точке области вытекает существование, а следовательно, и непрерывность производных всех порядков в той же области.

В частности, отсюда следует, что производная функции, аналитической в области G, есть функция, аналитическая в той же области.