Итерационные методы решения линейных уравнений

В итерационных методах предполагается осуществление трех следующих этапов: построение для вычисления последовательных приближений итерационного процесса, сходящегося к точному решению (т. е. построение последовательности векторов х⁽⁰ х<^{>, х^<2>, …, х^(к сходящейся к точному решению х*) определение критерия сходимости этого процесса, позволяющего определить момент достижения требуемой точности; исследование скорости сходимости и оптимизация итерационного процесса с целью уменьшения числа операций, необходимых для достижения требуемой точности.

Итерационные методы позволяют получить решение с наперед заданной точностью, если доказана сходимость метода. Строго точного решения итерационные методы не дают, поскольку оно достигается как предел последовательности векторов. Прямой метод, вообще говоря, дает точное решение, но из-за ошибок округления, имеющих место на любых компьютерах, оно не может быть достигнуто, и a priori даже трудно оценить, насколько это решение отличается от точного. В связи с отмеченным итерационные методы иногда позволяют получить решение с большей точностью, чем прямые.

Рассмотрим несколько итерационных методов решения линейных уравнений.

[ Метод простой итерации В методе простой итерации система (1.1) линейных алгебраических уравнений Ах — Ь приводится к эквивалентной системе вида.

Решение системы (1.9) и, следовательно, решение исходной системы (1.1) ищется как предел последовательности векторов при k -«.

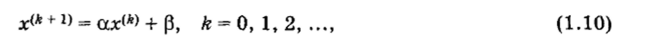
где л:⁽⁰⁾— начальное приближение для вектора решения.

Достаточное условие сходимости метода простой итерации определяется следующей теоремой.

ТЕОРЕМА 1. Если какая-либо норма матрицы а, согласованная с рассматриваемой нормой вектора х, меньше единицы (||а|| < 1), то последовательность x^w в методе простой итерации сходится к точному решению х* системы (1.9) со скоростью, не меньшей скорости геометрической прогрессии со знаменателем q < |)а|| при любом начальном приближении х^№>.

ДОКАЗАТЕЛЬСТВО Для доказательства теоремы введем погрешность е^(к) = х* — *^lk>. Вычитая из соотношения х* = ах* + р равенство (1.10), получаем е^{(<�г +} О = <�хе<*). Переходя к нормам, имеем.

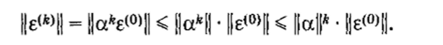
Отметим, что неравенство ||а*?⁽⁰⁾|| < ]]а*|] • ||е^<0,|| из предыдущего выражения является условием согласованности нормы матрицы и вектора. Если j|a (j < 1, то при любом векторе начальной погрешности (или иначе — при любом начальном векторе х⁽⁰⁾) норма погрешности ||е^{, к>}||*⁾ стремится к нулю не медленнее геометрической прогрессии со знаменателем q < ||a||.

Если в качестве нормы матрицы выбрать норму.

п п

||а ||_с = шах? |aJ или ||a 1^ = шах? |а₍ |, то для решения вопроса о сходимости метода простой итерации можно воспользоваться Верхний индекс k в скобках означает номер итерации, а без скобок, как обычно, степень.

следствием из теоремы 1: метод простой итерации сходится, если для матрицы, а выполняется одно из следующих условий:

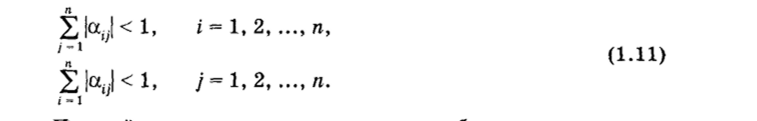
Простейшим и распространенным способом приведения системы Ах = b к виду (1.9), удобному для итераций, является выделение диагональных элементов, при этом каждое г-е уравнение разрешается относительно t-ro неизвестного:

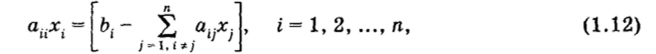
и метод простой итерации запишется в виде.

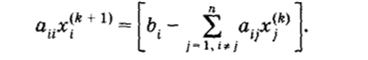
Матрица, а при этом имеет вид.

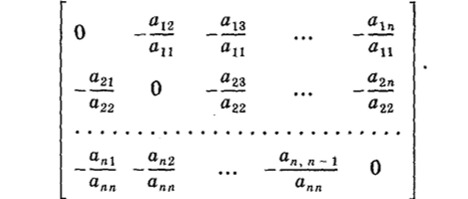
Элемент этой матрицы можно записать в виде а, = -^[1 — 5"],.

ч а" ч

где 5_j;. — символ Кронекера. В этом случае достаточное условие сходимости метода простой итерации может быть сформулировано как условие преобладания диагональных элементов матрицы А, что следует из (1.11) и записи матрицы а, т. е.

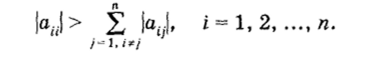
КРОНЕКЕР ЛЕОПОЛЬД (Kronecker Leopold; 1823— 1891) — немецкий математик, основные работы которого относятся к алгебре и теории чисел, теории квадратичных форм и теории групп, а также теории эллиптических функций. Большое значение имеют его исследования по арифметической теории алгебраических величин.

Еще раз подчеркнем, что рассмотренные формы условия сходимости метода итерации являются лишь достаточными. Их выполнение гарантирует сходимость метода, но их невыполнение в общем случае не означает, что метод простой итерации расходится. Необходимым и достаточным условием сходимости метода простой итерации является условие того, что целая часть |A._max| < 1 (где А_тах — максимальное по модулю собственное значение матрицы А); это условие редко используется в практике вычислений.

Перейдем к вопросу об оценке погрешности решения. Представляют интерес два соотношения оценки погрешности решения _е(*) = х* - х: первое связывает норму погрешности с нормой разности двух последовательных приближений Цх*** - х⁽* ~ ¹¹1| и может быть использовано для оценки погрешности только в процессе вычислений; второе связывает норму погрешности с нормами вектора начального приближения ||х^<0)|| и вектора свободного члена ||(3j| в системе (1.9). Необходимые соотношения даются следующими двумя теоремами.

ТЕОРЕМА 2. Если какая-либо норма матрицы а, согласованная с рассматриваемой нормой вектора х, меньше единицы (|)а|| < 1), то имеет место следующая оценка погрешности:

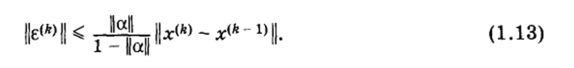
ДОКАЗАТЕЛЬСТВО. Вычтем из равенства х* = ах* + (3 равенство (1.10):

Вычитая из обеих частей значение приближения х⁽* ~ ¹⁾, преобразуем это соотношение к виду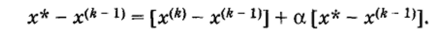

Перейдя к нормам, получим.

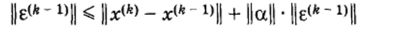
или.

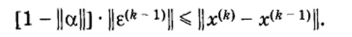
Так как по условию теоремы [1 — ||а||] > 0, то.

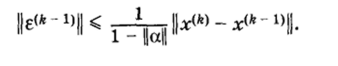
Используя соотношение е^№ = аг⁽* ¹⁾, из которого следует, что !|е⁽*)|| < ||а|| • ||е (1, окончательно получим:

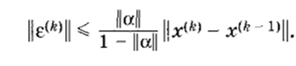
ТЕОРЕМА 3. Если какая-либо норма матрицы а, согласованная с рассматриваемой нормой вектора х, меньше единицы (||а|(< 1), то имеет место следующая оценка погрешности:

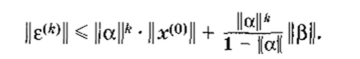
Сделаем два замечания. Во-первых, соотношение (1.13) может быть записано в виде.

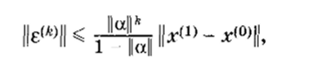
позволяющем получить оценку погрешности по результатам двух первых итераций. Во-вторых, при использовании метода итераций в качестве оценки погрешности вычислений иногда рекомендуется использовать норму разности двух последовательных приближений. Из соотношений для погрешности следует, что в общем случае это неверно. Если норма ||а|| близка к единице, то коэффициент при — х⁽* «'>|(может быть достаточно большим.

Погрешности последовательных итераций связаны соотношением.

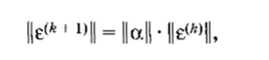
т. е. погрешность изменяется на шаге линейно. Говорят, что метод имеет линейную сходимость или первый порядок сходимости. Вместе с тем количество итераций, необходимое для достижения требуемой точности, зависит от значения ||а)| и начального приближения х.

Итак, на примере метода простой итерации продемонстрированы три этапа итерационных методов: построение последовательности векторов, порождаемых формулой (1.10); определение условия сходимости по теореме 1 и оценка скорости сходимости с помощью теорем 2 и 3.

| Метод Зейделя В методе простой итерации не используется кажущаяся очевидной возможность улучшения сходимости итерационного процесса — немедленное введение в расчет вновь вычисленных компонент вектора х<-^к). Эта возможность используется в итерационном методе Зейделя. Итерационный процесс для системы (1.9) выполняется при этом по соотношению.

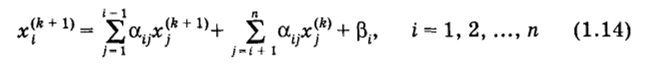
или для системы (1.1).

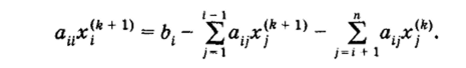
Не вдаваясь в подробности, отметим, что метод итераций Зейделя часто действительно приводит к более быстрой сходимости, чем метод простой итерации. Однако возможны случаи, когда метод итераций Зейделя сходится медленнее метода простой итерации, и даже случаи, когда метод простой итерации сходится, а метод итераций Зейделя расходится.

Отметим, что метод Зейделя сходится, если матрица А положительно определенная и симметричная.

Покажем, что метод итераций Зейделя эквивалентен некоторому методу простой итерации со специальным образом построенной матрицей, а и вектором 3 в соотношении (1.10). Для этого запишем систему (1.14) в виде х^{(к н} О = Нх^{(к +} О + F.+ 3, где F — верхняя треугольная матрица из коэффициентов матрицы а, a Н = а — F. Перепишем систему в виде (Е — Н)х^{(к +} «= Fx^w + 3.

где Е — единичная матрица. Матрица (Е — Н) — нижняя треугольная матрица с диагональными элементами, равными единице. Следовательно, определитель этой матрицы отличен от нуля (равен единице) и она имеет обратную матрицу (Е — Н)'¹, Тогда.

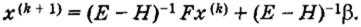
Сопоставляя это соотношение с решением (1.10), можем заключить, что действительно метод итераций Зейделя эквивалентен методу простой итерации в том смысле, что для установления условия и критерия сходимости метода итераций Зейделя можно воспользоваться теоремами, приведенными для метода простой ЗЁЙДЕЛЬ ФИЛИПП ЛЮДВИГ (Seidel Philipp Ludwig; 1821—1896) — немецкий астроном и математик, основные работы которого относятся к математическому анализу. Одновременно и независимо от Дж. Г. Стокса 3. ввел понятие равномерной сходимости последовательности и ряда. Им предложен итерационный метод решения системы линейных алгебраических уравнений (метод Зейделя).

итерации, если положить а ~ (Е — Н) ¹F. Итерационный процесс для системы (1.12) записывают и в более общей форме, а именно:

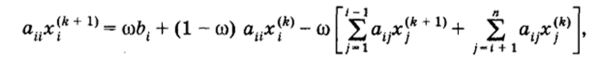
вводя в итерационный процесс для xj* ^{+ 1)} значение которое отсутствует в методе простой итерации и методе Зейделя.

Итерационный процесс при со > 1 называют МЕТОДОМ ВЕРХНЕЙ РЕЛАКСАЦИИ, при со = 1 (метод Зейделя) — методом ПОЛНОЙ РЕЛАКСАЦИИ и при СО < 1 — методом НИЖНЕЙ РЕЛАКСАЦИИ.

В простом случае при специально выбранном со можно дать оценку числа итераций N, необходимых для достижения заданной точности е. В методе простой итерации = 0,2n²ln (1/е), методе Зейделя N — 0,1п²1п (1/е), методе верхней релаксации N = 0,64п1п (1/е). Очевидно, что число итераций тем больше, чем больше порядок системы; при этом имеет место квадратичная зависимость в первых двух методах и линейная зависимость в методе верхней релаксации. Очевидно также, что число итераций тем больше, чем меньше е.

Представленные оценки не являются универсальными, и хотя в обсуждаемом случае самым медленным является метод простой итерации, а самым быстрым — метод верхней релаксации, это соотношение в других случаях может изменяться.

Можно дать наиболее общую запись итерационного процесса для системы (1.1). Имеем.

где В_к — некоторая матрица, выбираемая для обеспечения быстрой сходимости метода. Во многом она определяется конкретной системой (1.1) и искусством вычислителя. Говорят, что итерационный процесс стационарный, если В_к и 1_к не зависят от ft; в дальнейшем индекс ft при Вит опускается. Из (1.15) очевидно, что если итерационный процесс сходится, т. е. х^^{к + 1)} — —> О, то он сходится к решению системы (1.1).

Пусть матрицы D и L определены следующим образом:

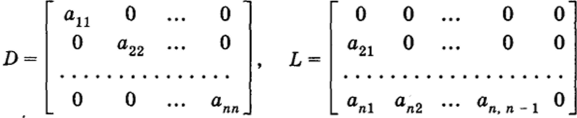
Тогда метод простой итерации есть частный случай процесса (1.15) при В = D и т = 1, метод Зейделя — частный случай при В = D + L, т = 1, а метод релаксации — частный случай при В = D + (йЬ, х = со.

Матрицу В_к следует выбирать как можно ближе к матрице А, но так, чтобы обращение этой матрицы было более простой задачей (матрица В — треугольная, трехдиагональная и т. д.).