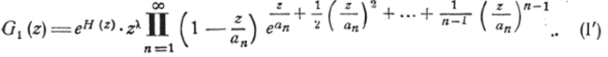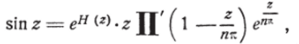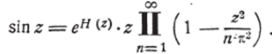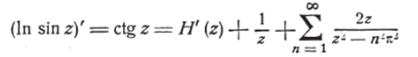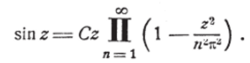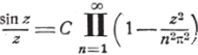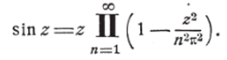Изображение целой функции в виде бесконечного произведения

В предыдущем пункте мы задавали a priori последовательность чисел (17), удовлетворяющую условию (18), и показали, что существует целая функция G (z), изображаемая формулой (1) Вейерштрасса, для которой данные числа служат нулями. Обратно, если мы имеем целую функцию G, (z) с бесконечным множеством нулей, то эти нули, как известно (гл. V, § 2, п. 6), не могут иметь никакой предельной точки, т. е. могут быть расположены в порядке возрастания их модулей в виде последовательности а_и а_ъ …" д_я, стремящейся к бесконечности при неограниченном возрастании п. Построив по формуле Вейерштрасса (I) целую функцию G (z)_% имеющую те же нули с той же степенью кратности, мы видим, что отношение.

будет изображать целую функцию у (z) [принимая <р (а_п)= lim ср (-гг)],.

г-*а_п

(p^f

не обращающуюся в нуль. В этих условиях выражение будет также целой функцией. Следовательно, мы имеем: у (z) = е** W₉ где И (z) означает некоторую целую функцию.

Наконец, из равенства (24) находим:

или.

Практически могут представляться значительные трудности при определении функции H (z) по данной функции G_{ (z). Так, например, пусть G_xz) — s z. Нули sinz будут: 2 =/пт, где п — любое целое число. Следовательно, согласно формуле (Г), мы можем написать:

где произведение распространяется на целые значения я, положительные и отрицательные. Здесь мы можем взять первоначальный фактор в упрощённом виде, потому что ряд сходится при /7 = 2.

Последнюю формулу для sinz мы можем, далее, упростить, группируя по два первоначальных фактора, соответствующих значениям я, равным и противоположным по знаку. Такая группировка вгтолне возможна, потому что нули ятг, будучи расположены в порядке возрастания их модулей, следуют в такой последовательности:

Таким образом, получаем:

Что касается определения целой функции H (z), то оно может быть сделано следующим образом. Составим логарифмические производные от обеих частей последней формулы:

%

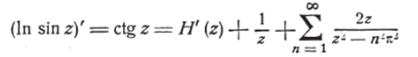
и сравним полученное соотношение с формулой (30') гл. VII, дающей представление функции cigz в виде бесконечного ряда простейших дробей. Тогда мы получим H'(z) = 0, откуда Н (z) = const. После этого формула для sin z примет вид:

Чтобы определить, наконец, постоянную С, образуем отношение.

и перейдём к пределу при z—? (). Тогда найдём: 1 =С. Следовательно, окончательная формула, представляющая sin z в виде бесконечного произведения, имеет вид: