Динамика материальной точки

Констатации того, как движутся частицы, чаще всего недостаточно — обычно требуется знать, почему они движутся так или иначе. На эти вопросы отвечает другой раздел механики — динамика, в котором изучают закономерности движения тел под действием сил. Динамика основана на законах И. Ньютона (1643—1727) — выдающегося английского физика, заложившего основы естествознания на базе работ предшественников, прежде всего Г. Галилея, Н. Коперника и И. Кеплера.

Если воздействий на тело нет или они друг друга компенсируют, то оно движется свободно. В системе отсчета, связанной с другим свободно движущимся телом, его движение имеет вид прямолинейного и равномерного, т. е. происходит с постоянной скоростью. Его называют движением по инерции. Закон инерции установили Г. Галилей и (независимо) французский философ, физик и математик Р. Декарт (1596—1650), однако он больше известен как первый закон Ньютона: тела сохраняют постоянную скорость, пока воздействие со стороны других тел не выводит их из этого состояния.

Этот закон выполняется только в инерциальных системах отсчета (ИСО), скорость которых постоянна, а системы отсчета, в которых он не выполняется, называют неинерциальными.

Во многих теоретических и практических задачах ИСО связывают с поверхностью Земли и называют лабораторной системой отсчета. Поскольку Земля вращается вокруг своей оси, то, строго говоря, это неправильно.

ВОПРОС. Велика ли ошибка?

ОТВЕТ. Нормальное ускорение поверхности Земли: а_п = v²/R, где R = R f osep, R₃ — радиус Земли на экваторе; ср — широта местности; v = 2kR/T, Т= 24 ч — период вращения Земли вокруг своей оси. Отсюда даже для экватора а_п = 4n²R₃/T=

= 0,033 м/с², что по отношению к ускорению свободного падения g составляет ~3%. Земля вращается также вокруг Солнца, однако нормальное ускорение ее орбитального движения еще меньше. Поэтому для большинства задач связывать ИСО с поверхностью Земли вполне допустимо, и в данном учебнике механическое движение рассматривается именно в лабораторной системе отсчета, если иное не оговорено.

Движение по инерции нарушается вследствие взаимодействия тел, меру которого предложил Р. Декарт, введя для этого понятие «сила». Под действием одной и той же силы разные тела получают разные ускорения, как бы по-разному сопротивляясь се действию. Это свойство материи названо инертностью. Мерой инертности является масса. Ее можно определить исходя из того, что под действием разных сил F_v F_v … одно и то же тело получает разные ускорения a_v a_v … При этом оказывается.

Именно эту константу принимают за инертную массу тела. Международный эталон массы в 1 кг (из платино-иридиевого сплава) хранится в Севре, расположенном вблизи Парижа.

Опыты показывают, что соотношение (1.32) справедливо при разных направлениях вектора F, т. е. в отличие от силы масса — величина скалярная. Ее распределение, но объему V тела характеризуют плотностью р. При равномерном распределении массы по объему.

Если же масса распределена неравномерно, то формула (1.33) определяет лишь среднюю плотность, а точное значение р = dm/dV. У воды, например, р ~ 1 г/см³, в центре Земли р ~ 10 г/см³, в центре Солнца р ~ 10² г/см³, а у нейтронных звезд р ~ 10¹⁵ г/см³.

Масса определяет ускорение тела, сонаправленное с действующей на него силой. В соответствии со вторым законом Ньютона.

т.е. ускорение, приобретаемое телом под действием силы, пропорционально силе и обратно пропорционально массе тела.

Итак, ускорение определяется через силу, которая его вызывает. В то же время сила — это мера взаимодействия тел, определяемая ускорением свободного тела либо деформацией несвободного. В уравнении (1.34) предполагается последнее, чтобы ускорение не определялось само через себя. Уравнение (1.34) называют также уравнением движения материальной точки. В нем F — это результирующая сила:

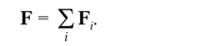
Закон (1.34) постулируется, т. е. ниоткуда не выводится. Он получен гением Пыотона на основе логического анализа и обобщения результатов многочисленных наблюдений и научной интуиции.

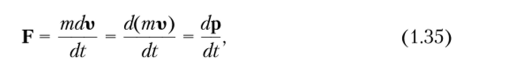
где р = mv есть импульс. Из формулы (1.35) следует соотношение Пользуясь равенством (1.7), формулу (1.34) можно представить также в виде.

Произведение Fdt называют импульсом силы. Формулы (1.35), (1.35') имеют более общий вид, чем (1.34), поскольку включают и те случаи, когда масса зависит от времени. Уравнение (1.35') формирует и некоторую симметрию в отношении терминологии: импульс силы, действующий на частицу, равен приращению импульса частицы.

Уравнение (1.34) определяет единицу силы ньютон: 1 Н = 1 кг-м/с², а она, в свою очередь, определяет другие производные единицы, например давления:

где F — модуль силы, нормальной к поверхности площадью 5. Единица давления паскаль (Па) названа в честь французского математика, физика и философа Б. Паскаля (1623—1662): 1 Па = 1 Н/м². Кроме основных и производных единиц СИ, стандарт разрешает применять десятичные кратные (кило-, мегаи т.д.) и дольные (милли-, микрои т.д.) единицы, а также некоторые внесистемные единицы, например минута, литр.

Характер взаимодействия тел (независимо от природы этого взаимодействия) выражает третий закон Ньютона: силы взаимодействия тел равны по модулю и направлены в противоположные стороны вдоль общей прямой.

Законы Ньютона легли в основу бурного развития техники и казались всеобъемлющими. Еще X. Гюйгенс утверждал, что все природные явления в конечном счете сводятся к механике, и такая точка зрения стала основой философского направления, названного «механицизм», или «механический детерминизм». Время внесло в него существенные коррективы, но не умалило ценности законов Ньютона, до сих пор позволяющих решать множество практически важных задач, в том числе в военном деле.