Лагранжа—Кольца. 
Вариационное исчисление и методы оптимизации

В самом общем случае задача Лагранжа—Вольца для нескольких функций z_k(k= 1,2,…, п) двух независимых переменных предполагает рассмотрение функционала вида.

где, как и прежде,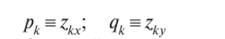

— частные производные функций z_k соответственно по х и у.

Если в функционале (6.60) функция g = 0, то имеем задачу Лагранжа, если же/= 0, то получаем задачу Майера.

Рассмотрим общую задачу Лагранжа—Вольца для п функций Z_k(x, у) (А: = 1,2,…, п): в общем случае эти функции не независимы, поскольку часть из нихдолжна удовлетворять дифференциальным уравнениям-связям:

причем т < п.

В рассматриваемой общей постановке граница дО. области Q определяется граничной линией, описываемой в плоскости (х, у) функцией у (х), и также в общем случае должна удовлетворять дифференциальным условиям-связям:

(здесь у' — производная указанной функции у (лг), которая определяется в процессе решения задачи).

Определим допустимую совокупность поверхностей z_k(x, у) как совокупность функций, непрерывных вместе с первыми производными всюду в области й, за исключением конечного числа линий (где производные терпят разрывы), которые удовлетворяют дифференциальным соотношениям внутри области (6.61) и условиям на границе (6.62).

Так же как и ранее, видим, что условия (6.61) и (6.62) более сильные, чем изопериметрические, поскольку они являются «поточечными». Переходя к рассмотрению постановки вариационной задачи, напомним, что из п искомых функций z_k(x, у) т связаны с дифференциальными уравнениями (6.61), тогда как п—т независимы в й. Последнее означает, что из всей совокупности вариаций 6z_k(x, у) свободными являются только п—т вариаций, тогда как т остальных требуют согласования посредством уравнений (6.61). Эти же рассуждения переносятся и на проблему определения граничной линии области на основе п + 1 функций z_k (х) иу (х), которые обязаны удовлетворять q условиям (6.62). При этом здесь также n+—q вариаций бz_k(x) и 6у (х) являются независимыми на граничной линии, тогда как остальные q из них на этой линии связаны уравнениями (6.62).

Параметры п—т и л+1 —q называют степенями свободы задачи в области й и на ее границе с? й.

Далее поступаем так же, как и ранее при рассмотрении задачи Лагранжа—Больца для функций одного независимого переменного (п. 3.4). Умножим каждое из уравнений (6.61) на соответствующий неопределенный множитель Лагранжа (х, у) (/ = 1, 2,…, т), а каждое из уравнений (6.62) — на числовой неопределенный множитель p_s (s = 1, 2,…, q), и суммируя каждую из групп построенных произведений, получим.

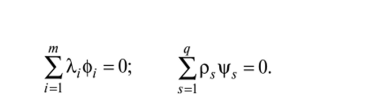
Проинтегрировав первую сумму по всей области Q, а вторую — соответственно вдоль контура dQ, найдем:

Вновь отметим, что каждое из соотношений (6.63) справедливо при любом выборе функциональных Х.(х, у) и числовых р. множителей Лагранжа.

Теперь на основе исходного функционала (6.60) и соотношений (6.63) построим расширенный функционал:

где функции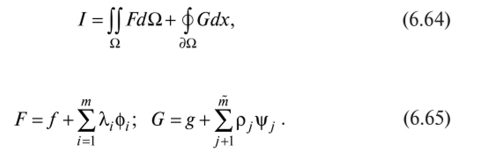

Рассматривая первую вариацию функционала (6.64) с функциями (6.65), можно построить систему необходимых условий на основе тех подходов, которые были применены ранее в данном разделе. Вместе с тем здесь необходимо помнить о том факте, что дифференциальные ограничения (6.61) и (6.62) привносят важные изменения в систему вариаций, а тем самым и в построение необходимых условий. Действительно, например, из п вариаций 6z_k(x, у) внутри области ?2 свободны только п~т. Аналогично на граничной линии свободными являются д+1 —q вариаций 6у (х) и бz_k(x), тогда как остальные q связаны ограничениями.

И здесь мы вновь используем тот прием, который применили при рассмотрении задачи Лагранжа—Больца для обыкновенных дифференциальных уравнений в разд. 3, подчеркивая при этом, что этот прием опирается на свободу выбора множителей Лагранжа. Следуя этому подходу, выберем т множителей Лагранжа {х, у) (/ = 1,2, …, т) таким образом, чтобы удовлетворялисьт уравнений Эйлера—Лагранжа:

Тогда в первой вариации функционала (6.64) будет содержаться п—т независимых вариаций bz_k (к = т + 1, т + 2,п):

Приравняем к нулю коэффициенты, при вариациях бz_k в (6.67) получаем п~т уравнений Эйлера—Лагранжа:

Таким образом, уравнения (6.66) и (6.68) дают в общей сложности п уравнений Эйлера—Лагранжа, которые в совокупности с т уравнениями (6.61) позволяют определить т функциональных множителей Лагранжа {х, у) и п поверхностей z,_k (х, у).

Совершенно аналогично определяем и функции на границе dQ, т. е. отвечающую ей функцию граничной линии у (х) со значениями Z_k(x) на ней, д ля чего также требуется найти q числовых множителей Лагранжа р_;. Здесь вновь имеем п +1 -ц свободных вариаций Ьу (х) и бz._k(x), тогда как остальные q вариаций связаны ограничениями (6.56). Таким образом, для нахождения q множителей Лагранжа р_;. и п + 1 функций z_k(x), у (л') имеется п + 1 + q соотношений.

Если в нашей задаче есть линии разрывов производных р_к и q_k, т. е. линии изломов поверхностей, то на них выписываем условия Эрдманна—Вейерштрасса, которые были получены в п. 6.3 и в общем случае имеют вид (6.51)—(6.53).

Условие Лежандра и неравенство Вейерштрасса также обобщаются для рассматриваемого случая по аналогии с несколькими функциями двух независимых переменных, рассмотренными в п. 6.3, и имеют тот же вид, что и соответствующие формулы (6.54) и (6.55).

Вместе с тем применение условия Лежандра и неравенства Вейерштрасса требует принятия во внимание имеющихся в задаче дифференциальных ограничений. Действительно, условие Лежандра должно быть согласовано с любой системой слабых вариаций бр_к и 6с/_к (к = 1,2,…, п), характер которых определяется дифференциальными уравнениями-связями (6.61). Говоря иначе, условие Лежандра должно быть дополнено соотношениями.

которые характеризуют малые возмущения решений уравнений (6.61) и отвечают слабым вариациям.

Аналогично неравенство Вейерштрасса должно выполняться для всей системы сильных вариаций наклонов величин Ьр_к и 6с/_к (к = 1, 2,…, п), опять-таки согласующихся с условиями (6.61). Согласующие соотношения обязаны удовлетворять такой системе уравнений:

где параметр к принимает значения от 1 до п.

Вид системы уравнений (6.70) обусловлен тем, что дифференциальные уравнения (6.61) должны выполняться для любых значений вариаций наклонов Ьр_к и 6с/_к.

Замечание 6.7. Безусловно, здесь было бы уместно привести примеры решения каких-либо пространственных задач. Однако мы перенесем такую возможность в следующий раздел, поскольку решение практически важных задач обусловлено тем обстоятельством, что на практике в таких задачах мы должны иметь дело с некоторыми функциями z_k (х, у) специального вида, называемыми управляющими. Этому посвящен следующий раздел.

Замечание 6.8. В продолжение предыдущего замечания отметим следующее. Пункт 6.4 и особенно его часть, посвященная задаче Лагранжа—Больца, может показаться «страдающей» чрезмерной общностью. Говоря иначе, мы не привели конкретных примеров решения задач Лагранжа или Лагранжа—Больца для уравнений с частными производными. Это обстоятельство связано исключительно с многообразием и трудностью постановок таких задач в практически важных случаях. И этот пробел мы компенсируем в следующем разделе.