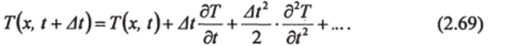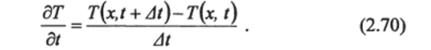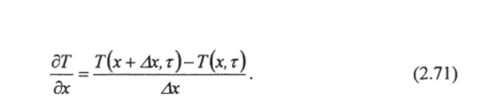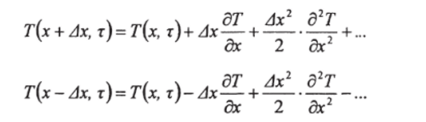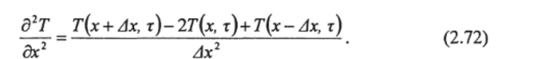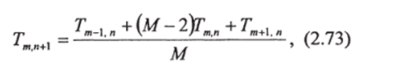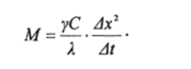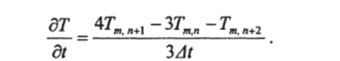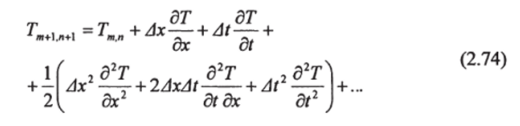Пример решения уравнений в частных производных

Уравнения в частных производных приводятся к разностному виду посредством ряда Тейлора [2].

Рассмотрим дифференциальное уравнение теплопроводности:

где х — координата точки, Т — температура, t — время, д — теплопроводность, С — теплоемкость, у — плотность.

Разложим функцию Т (х, /) в степенной ряд по /, считая х постоянным:

Поскольку At мало, то членами ряда At² и более высокими степенями можно пренебречь и в первом приближении вместо можно взять:

Аналогично:

Для получения первого приближения используем два следую;

дх

щих разложения в ряд:

Если сложить эти формулы и отбросить члены, содержащие Ах в степени выше 2, то получим:

Предположим, что отыскивается решение дифференциального уравнения (2.68) в области S> представленной на рис. 2.6.

Покроем эту область сеткой прямоугольников со сторонами Ах и At будем находить функцию Т в узлах этой сетки.

Примем следующие обозначения:

При этих обозначениях формулы (2.70−2.72) примут следующий вид:

Подставив эти выражения для производных в дифференциальное уравнение (2.70). Мы придем к следующему уравнению в конечных разностях:

Если известны значения функции Т в точках (m -1, л), (/л, л), (тл+1, л), то по формуле (2.73) можно найти значение Г в точке (т, л+1).

Пусть требуется найти лучшее приближение к —, чем в уравнении.

dt

(2.70). Разложим Т{х, t + 2At) в ряд:

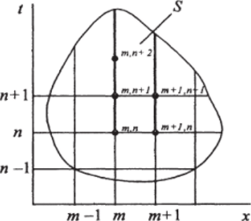
Рис. 2.6. Пример решения уравнения (2.70) с помощью ряда Тейлора.

решая которое относительно Т_{т л+|}, найдем:

где.

Вычитая из этого ряда равенство (2.69), умноженное на 4, и пренебрегая членами, содержащими At в степени выше второй, получим: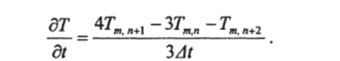

Это приближение является лучшим по сравнению с (2.70).

Далее, пусть требуется найти приближение в конечных разностях для.

——. Используем ряд Тейлора: dt дх

_ _… ет д²т дт д²т

их соответст;

Заменив в уравнении (2.74) —, —г , — и —г;

дх дх² dt 8t²

_в, дТ д²Т

вующими приближениями в конечных разностях (например, и —.

выражениями из формул (2.70) и (2.72)), найдем:

Подобные методы могут быть использованы и для получения приближений к производным более высоких порядков.