Расчет нагрузок на основе методов теории случайных функций

Сделаем некоторые краткие замечания по поводу используемых в дальнейшем методов расчета, рассмотрев более подробно характер поведения нагрузок. Следует сразу же отметить, что в большинстве случаев нагрузки не являются детерминированными, т. е. принимающими определенные значения для фиксированных физических координат системы и времени.

Рассмотрим, например, тягу двигательной установки. На маршевом (для определенности) участке работы двигателя принято считать, что тяга определяется параметрами двигательной установки и временем ее работы и может быть рассчитана по простейшим алгебраическим зависимостям. Такое упрощение реального поведения тяги является моделью действительно существующего ггроцесса. В действительности, тяга — это случайная функция времени, так как случайными являются все геометрические и физические параметры двигательной установки. В самом деле, диаметр критического сечения сопла, например, не может быть изготовлен абсолютно точно. Он имеет заданный допуск, и отклонения от номинального значения подчиняются нормальному закону распределения. Аналогичные явления наблюдаются и при определении других нагрузок: массовых, аэродинамических, ветровых и т. д. Таким образом, в большинстве случаев нагрузки являются случайными функциями координат и времени.

Рассмотрим случайную функцию R (t), значение которой при любом 1 является случайной величиной. Аргумент t (не обязательно время) будем считать величиной неслучайной — детерминированной.

Пусть проведено п опытов для определения R (t) и в результате получено п кривых, ординаты которых для фиксированного аргумента нс совпадают. Для этого значения аргумента можно определить п значений /?() и построить закон распределения ординат R ( /|). Зная закон распределения, нетрудно определить математическое ожидание — среднее значение функции в момент и дисперсию, характеризующую отклонение случайной величины от ее среднего значения. Однако среднее значение и дисперсия вычислены для фиксированного аргумента /₍ и поэтому не могут охарактеризовать поведение случайной функции для всего рассматриваемого промежутка изменения аргумента.

Очевидно, необходимо взять еще несколько фиксированных значений аргумента и построить соответствующий многомерный закон распределения случайной величины. Указанный способ не всегда удобен из-за своей громоздкости, поэтому в теории случайных функций ограничиваются чаще всего расчетом параметров, которые характеризует закон ее распределения. В качестве таких параметров обычно принимают моменты случайной величины первого и второго порядка. Момент первого порядка Д (0 = Лф (0] - математическое ожидание ординаты случайной функции при произвольном значении аргумента Л Функция R (t) уже не является случайной величиной.

Центральные моменты второго порядка:

ф (0]=лф (/)-Л (/)П — дисперсия случайной величины /?(/),.

K (_ti, t₂)= лф (/,) — R (/,)][Д (/₂ )-R (h)]} - момент связи случайных величин R ( 1_{) и R (1₂), называемый корреляционной функцией.

Если известен дифференциальный закон f (R/t) распределения случайной величины R (l), то.

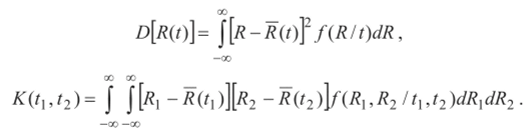
Раздел теории случайных функций, в котором оперируют только моментами первых двух порядков, носит название корреляционной теории случайных функций.

Случайные функции принято разделять на следующие группы:

• 1) стационарные и нестационарные, их свойства зависят от момента времени, с которого начинается отсчет;
• 2) с нормальным законом распределения для фиксированного значения аргумента и ненормальным;
• 3) марковские, для которых вероятностные свойства в последующий промежуток времени полностью определяются значением ординаты этой функции в заданный момент времени и не зависят от ее значений в предыдущие моменты времени, и не марковские.

На практике встречаются следующие типы задач, которые требуют привлечения аппарата теории случайных функций:

• 1. По заданным свойствам случайных функций необходимо определить вероятностные характеристики процесса, например дисперсию ординаты случайной функции. Примером такого рода задач может служить определение отклонения тяги от ее среднего значения или определение рассеивания точек падения головной части.
• 2. Ко второй группе относят задачи, в которых вероятностные характеристики определяются по экспериментальным данным. Здесь используются обычные способы обработки опытных данных, применяемые в теории случайных величин, с той лишь разницей, что учитывают зависимости между ординатами реализаций (опытов) случайных функций.
• 3. Искомые случайные функции описываются дифференциальными зависимостями, и задачи обычно сводятся к определению вероятностных характеристик случайных функций, получаемых на «выходе» системы, по вероятностным характеристикам случайных функций, поступающих на ее «вход».

В любой из указанных задач поведение исследуемой величины достаточно полно может быть охарактеризовано ее математическим ожиданием, дисперсией и корреляционной функцией.

При дальнейшем изложении будет использован детерминированный подход к расчету нагрузок, в котором фактически определяется лишь среднее значение нагрузки и не рассматриваются ее вероятностные характеристики. Следует еще заметить, что вероятностный подход на базе случайных функций может быть применен и к расчету напряженного состояния конструкции, когда соответствующие напряжения и деформации считаются случайными функциями.