Математическая обработка и прогнозирование информации, измеренной в неметрических шкалах

Измерять информацию необходимо для того, чтобы ее можно было сравнивать, оценивать, выявлять закономерности и т. п. — без измерения невозможно познание. В то же время необходимо отметить, что указанные приемы не всегда непосредственно применимы к собранной и измеренной информации. Например, сравнивать информацию, собранную и измеренную в номинальной шкале, не имеет смысла и нет такой возможности, поскольку номинальная шкала позволяет только отнести измеренный объект к тому или иному классу. Название, наименование класса не может быть предметом статистической обработки и уж тем более — сравнения.

Каждой шкале измерения присущ свой оригинальный набор методов обработки информации. Применение инструментария, рассчитанного на другой тип шкалы, в большинстве случаев приводит к ошибочной интерпретации результатов. При этом следует отметить, что методы обработки информации, измеренной в номинальной шкале, могут быть использованы для обработки информации, измеренной в шкале более высокого уровня, например, порядковой. Но методы, с помощью которых обрабатывается информация, измеренная в порядковой шкале, не всегда могут быть использованы для обработки информации, измеренной в шкале номинальной.

В простейшей номинальной шкале моделируются самые простые действия с информацией — отношения «равенства — неравенства». Эта шкала обладает только характеристикой описания — дается множество элементов, из которых следует указать один элемент, причем как результат идентификации, а не сравнения.

С информацией, измеренной по номинальной шкале, можно осуществлять только действия по отнесению объекта с измеренным признаком к тому или иному типу объектов. Это означает, что с помощью идентификации объектов при использовании номинальной шкалы можно осуществлять группировку объектов, и это имеет большое значение, ведь наиболее мощным инструментом современного научного анализа как раз и выступает метод типологизации — мысленное расчленение сложной совокупности объектов наблюдения на устойчивые типы, состоящие в свою очередь из классов, групп, родов и т.н. Чаще всего эту процедуру называют классификацией или группировкой, поскольку типологизация — высшая таксономическая категория, результат не только простой, пусть и многомерной группировки, но и аналитических исследований.

Классификацией называется распределение объектов по тому или иному существенному свойству, в результате чего каждый из них попадает в точно указанный класс, подмножество или группу^[1].

Одним из наиболее часто используемых методов классификации объектов, информация о которых приводится в номинальной шкале, является кластерный анализ. При этом структурирование группы осуществляется «снизу доверху»^[2]: вначале предполагается, что каждый объект образует самостоятельный кластер, а затем производится слияние близко стоящих кластеров в более крупные кластеры (до получения кластера, объединяющего рассматриваемую группу). На каждом этапе слияния объединение происходит на основе нового признака классификации (например, вначале создаются кластеры по национальности респондентов, затем — но уровню полученного образования и т.н.).

Если обозначить измерение каждого объекта буквами алфавита (А, Б и т. д.), то символическая запись номинальной шкалы будет иметь вид.

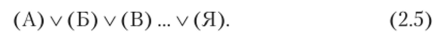
Здесь знак v означает дизъюнкцию, т. е. операцию «либо — либо».

Номинальная шкала позволяет выполнять следующие операции^[3].

• 1. Нахождение частот распределения по пунктам шкалы с помощью проецирования или в натуральных единицах.
• 2. Поиск средней тенденции, но модальной частоте. Модальной называют группу с наибольшей численностью.
• 3. Установление взаимосвязи между рядами свойств с помощью перекрестных таблиц.

Следует обратить внимание на то, что данные операции производятся не с самими числами, измеренными в этой шкале, а с количеством наблюдений объектов, обладающими теми или иными признаками и отнесенными в отдельные группы. Количество наблюдений или элементов, отнесенных к той или иной группе, — это уже информация, измеренная в метрической шкале, с которой можно работать всеми доступными и уместными математическими методами.

Для того чтобы определить частоту распределения каждой группы, вычисляется численность элементов каждой из групп, а затем находится отношение этой численности к общему числу единиц признаков. Пусть, например, в группу с высшим образованием из числа респондентов в 500 человек были отнесены 133 человека. Тогда частота респондентов с высшим образованием в данной выборке составит 133 / 500 = 0,266. Эта величина дает исследователю дополнительную информацию (например, что число людей с высшим образованием составляет 26,6%). Частоту распределения удобно анализировать с помощью различного рода диаграмм — столбиковых, ленточных или круговых.

В статистике под «модой» понимают наиболее часто встречающееся значение. В номинальной шкале мода характеризует группу с наибольшей численностью. Вычисление модальной группы не вызывает затруднений, так как требует выполнения только операции сравнения типа «больше — меньше». Если в имеющейся выборке есть только одна модальная группа, то говорят об «унимодальной» группе. Значительно реже встречаются случаи, когда две и более группы включают одинаковое число единиц, которое для данной выборки является максимальным. В этом случае говорят о многомодальных случаях. Наличие нескольких мод говорит о своеобразии имеющегося распределения. Их анализ позволит получить дополнительную информацию.

Важным способом количественного анализа информации является установление взаимосвязи между рядами свойств с помощью таблиц сопряженности признаков. Здесь также используется информация о количестве наблюдаемых признаков. Эти количественные значения позволяют оценить возможность наличия взаимосвязи между наблюдаемыми признаками. Информацию о количестве наблюдаемых признаков сводят в таблицу сопряженности так, как это сделано в табл. 2.11.

Таблица 2.11

Общий вид таблицы сопряженности для анализа взаимосвязи между признаками.

Используя обозначения, приведенные в табл. 2.11, можно рассмотреть оценку взаимосвязи между наблюдаемыми признаками. Наиболее простым в использовании является коэффициент ассоциации Юла. С учетом введенных нами обозначений он имеет вид.

Этот коэффициент изменяется в пределах от -1 до +1. Чем ближе коэффициент по модулю к единице, тем сильнее связь между измеренными признаками. Если он имеет отрицательное значение, то это свидетельствует о том, что увеличение значений одного признака приводит к уменьшению значений другого.

Пример Любой студент российского вуза может обладать одним из признаков — мужским или женским полом. Можно выяснить еще одну характеристику — состоит или не состоит в браке. Здесь важно, что шкала наименований дает исчерпывающие состояния — ни в том, ни в другом случае нельзя предложить хотя бы один дополнительный класс, к которому может быть отнесен студент (при измерении свойства «принадлежность к полу» у студентов может быть только одно из двух состояний — принадлежность либо к мужскому, либо к женскому полу).

По признакам принадлежности к тому или иному полу, а также по отношению к браку можно выделить четыре сопряженные группы, условные данные о которых представлены в табл. 2.12.

Именно количество измеренных в номинальной шкале данных и подвергается статистической обработке. Это количество, очевидно, измеряется в метрической шкале.

Таблица 2.12

Условный пример таблицы сопряженности.

Для нашего условного примера коэффициент Юла будет равен.

_Л 34 62−66−88 _Л/Л_.

О =-= —0,467;

^ 34−62 + 66−88.

Это говорит о слабости возможной зависимости между признаками. Знак «минус» можно проинтерпретировать так: при переходе от признака «мужской пол» к «женскому полу» не следует ожидать перехода у объекта свойства «состоит в браке» к свойству «не состоит в браке», а наоборот, следует ожидать появления противоположного признака «состоит в браке».

Поскольку взаимосвязь между признаками все же имеется, можно получить дополнительную информацию о наблюдаемом явлении для получения элементарных прогнозов, например, для прогнозирования того, состоит ли студент в браке или нет.

Для этого преобразуем табл. 2.12 к значениям в процентах от общего числа наблюдаемых (табл. 2.13).

Таблица сопряженности в процентах.

Таблица 2.13

По данным этой таблицы можно утверждать следующее.

• 1. Если перед нами студент, то в 49 случаях из 100 — это мужчина, а в 51 случае — женщина.
• 2. Зная, что перед нами студент, у объекта с этой характеристикой мы можем ожидать, что в 40 случаях из 100 он будет состоять в браке, а в 60 случаях — нет.
• 3. Если перед нами студент мужского пола, то в 14 / 49 = 28 случаях из 100 он будет холост.
• 4. Если перед нами студентка, то в 26 / 51 =52 случаях из 100 она окажется замужем.

Таким образом, измерение информации в номинальной шкале оказывается полезным для прогнозирования социально-экономических процессов, поскольку мы можем по количеству наблюдаемых признаков давать количественные характеристики взаимосвязи между показателями и получать некоторые прогнозные оценки.

Недостаток коэффициента ассоциации Юла заключается в том, что он не очень точно оценивает взаимосвязь между факторами. Если, например, хотя бы в одной клетке таблицы сопряженности будет иметься нуль, то коэффициент ассоциации Юла будет равен единице, но это не говорит об однозначной зависимости между признаками.

От этого недостатка свободен коэффициент хи-квадрат Пирсона:

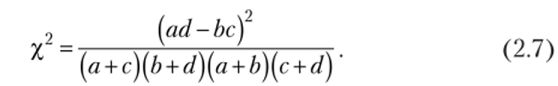
Поскольку он лежит в пределах от нуля до единицы, трудно дать интерпретацию его значениям, к тому же он не указывает на направление взаимосвязи между признаками. Поэтому значительно чаще на практике вместо него используют корень квадратный из этой величины, который получил название «коэффициент сопряженности Пирсона»:

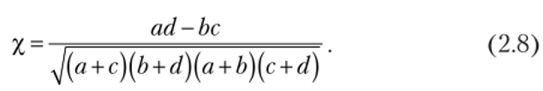
Из анализа этих формул следует, что коэффициенты Пирсона могут принимать значения от -1 до +1. При этом значение -1 коэффициент будет иметь только в том случае, когда а = d= 0, а значение +1 — когда b = с = 0.

Пример Вычислим коэффициенты хи-квадрат и сопряженности Пирсона применительно к условным данным табл. 2.12. Получим для коэффициента хи-квадрат:

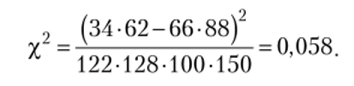
Как видно, дать интерпретацию этим значениям сложно. А близость коэффициента к нулю, казалось бы, свидетельствует о том, что взаимосвязи нет, хотя из анализа таблицы некое представление о наличии взаимосвязи все-таки остается. Рассчитаем коэффициент сопряженности Пирсона:

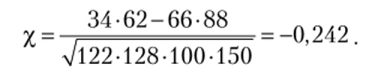
Значение коэффициента невелико, ближе по модулю к нулю, чем к единице. Это свидетельствует о том, что связь между группами признаков есть, но довольно слабая. Знак «минус» говорит об обратной зависимости между признаками и подтверждает выводы, которые были получены с помощью коэффициента Юла.

Как видно из приведенных примеров, степень связи между признаками довольно сложно выявить однозначно. Как и в случае с корреляциями между признаками, измеренными в метрической шкале, логика использования этих коэффициентов должна быть такой: вначале следует аналитическими методами обосновать наличие взаимосвязи между признаками, а затем подтвердить эту гипотезу с помощью коэффициентов Юла или Пирсона. Следует отметить, что коэффициент сопряженности Пирсона всегда меньше коэффициента Юла. Обычно рекомендуется придерживаться следующего эмпирического правила: можно говорить о том, что взаимосвязь подтверждается, если коэффициент Юла по модулю больше 0,5, а коэффициент сопряженности Пирсона — больше 0,3.

На основе статистики хи-квадрат (2.7) были разработаны и другие коэффициенты, отражающие некую связь между двумя величинами (например, коэффициент сопряженности и коэффициент Крамера). Но от рассмотренного нами коэффициента (2.8) они отличаются несущественно и имеют схожий смысл, поэтому подробно останавливаться на них мы не будем.

Выше мы проанализировали ситуации изучения связи между двумя бинарными переменными, но может возникнуть закономерный вопрос: как быть в случае с категориальными переменными, принимающими больше чем два значения? В этом случае строить таблицу сопряженности по самим переменным не имеет смысла, так как в номинальных переменных нет упорядочения, а любая рассчитанная характеристика показывает связь между тем, как упорядочены элементы в одном признаке и элементы — в другом. Поэтому прежде чем строить таблицу сопряженности по категориальной переменной, эту переменную надо разбить на ряд бинарных.

Пример Прогнозист салона «Мега-моторс» собрал данные о том, какие машины пользуются спросом. В этих данных есть два интересующих его признака.

• 1. Цвет машины:
  • • желтый;
  • • красный;
  • • черный;
  • • другой.
• 2 Тип кузова:
  • • седан;
  • • хэтчбэк;
  • • универсал.

По этим данным прогнозист составил следующую таблицу сопряженности (табл. 2.14).

Таблица 2.14

Таблица сопряженности в частотах, но тинам автомобилей.

Из таблицы следует, что «другой» цвет — самая многочисленная группа. Можно также сделать вывод, что черный седан и красный универсал пользуются популярностью среди покупателей. Однако рассчитывать по этой таблице коэффициенты Юла и Пирсона нельзя: они будут показывать, как при переходе от черного цвета к «другому» будут меняться предпочтения от хэтчбэка в пользу универсала, что абсолютно бессмысленно. Поэтому каждую из этих переменных надо разбить на бинарные:

• 1. Желтая машина:
  • • 1 — если выбрана желтая машина;
  • • 0 — если не выбрана желтая.
• 2. Красная машина:
  • • 1 — если выбрана красная машина;
  • • 0 — если не выбрана красная.
• 3. Черная машина:
  • • 1 — если выбрана черная машина;
  • • 0 — если не выбрана черная.
• 4. Другой цвет:
  • • 1 — если выбрана машина другого цвета;
  • • 0 — если не выбрана машина другого цвета, и
• 1. Седан:
  • • 1 — если выбрана машина с кузовом седан;
  • • 0 — если не выбрана машина с кузовом седан.
• 2. Хэтчбэк:
  • • 1 — если выбрана машина с кузовом хэтчбэк;
  • • 0 — если не выбрана машина с кузовом хэтчбэк.
• 3. Универсал:
  • • 1 — если выбрана машина с кузовом универсал;
  • • 0 — если не выбрана машина с кузовом универсал.

На основе этих новых переменных можно составить таблицы сопряженности и рассчитать коэффициенты Юла и Пирсона. Пример одной из таких таблиц (черных машин с кузовом седан) — табл. 2.15.

Таблица 2.15

Таблица сопряженности в частотах по типам автомобилей для черных седанов.

По данным этой таблицы коэффициент Юла составил 0,689, а коэффициент Пирсона — 0,361. Эти значения указывают на то, что между выбором черного цвета и седана есть некоторая связь. Интерпретироваться она может следующим образом: люди, покупающие машины с кузовом седан, отдают предпочтение черному цвету кузова.

Кроме того, на основе данных табл. 2.14 можно оценить, какие машины пользуются наибольшей популярностью у потребителей. Например, среди красных автомобилей наибольшей популярностью пользуется универсал, поэтому при решении о том, какие автомобили салопу закупать в большем количестве, имеет смысл сделать акцент на автомобили этого типа.

Для номинальной шкалы измерения информации имеется возможность вычисления важной статистической характеристики — моды. Например, для рассмотренных выше условных примеров совокупности признака «мужской пол» модой является состояние «не состоит в браке», а для признака «женский пол» модой является состояние «состоит в браке». Для признака «состоит в браке» модой является состояние «женский пол», а для признака «не состоит в браке» — «мужской». Все эти моды при использовании принципов индукции могут служить основаниями для выполнения элементарных прогнозов.

Итак, операции с информацией, измеренной в номинальной шкале, позволяют исследователю выполнить некоторые прогнозы. Значительно больше знаний и выводов об объекте прогнозирования можно получить, если собрана и измерена информация в шкалах более высокого уровня. Разнообразнее становятся и инструменты прогнозирования.

Шкала порядка (ранговая шкала) наряду с описанием имеет еще и порядок, в результате чего возможно установление приоритетов и сравнений информации. Помимо операции типа «равенство — неравенство» с величинами, измеренными в шкале порядка, выполняются действия типа «больше — меньше». Кроме операции отнесения объекта по информации о нем к тому или иному классу, появляется возможность сравнения этой информации по какимлибо признакам на предмет того, какой признак оказывается больше другого. При этом шкала порядка имеет тем или иным образом сформированные ранги. Поэтому вместе с методами обработки данных, применимыми для шкалы наименований (номинальной шкалы), выполняются и другие действия, поскольку здесь есть некоторые количественные признаки. Например, рост двух количественных признаков уже может помочь более точно оценить наличие возможной взаимосвязи между признаками, чем это получается сделать с информацией, измеренной в номинальной шкале.

Работая с информацией, измеренной в этой шкале, необходимо помнить, что интервалы в ней не равны друг другу и, вообще говоря, интервалами не являются, а числа означают лишь порядок следования признаков.

С числами в шкале порядков можно выполнять следующие действия^[4].

• 1. Числа могут быть монотонно преобразованы в другие числа.
• 2. Возможно суммирование оценок по ряду упорядоченных шкал.
• 3. Помимо моды Мо появляется возможность рассчитать медиану Me.
• 4. Взаимосвязь между признаками может быть определена с помощью коэффициентов ранговой корреляции.

Поясним суть каждого действия. Прежде всего, рассмотрим монотонное преобразование чисел порядковой шкалы. С учетом того, что числа в ранговой шкале означают лишь порядок следования признаков, то сам порядок можно обозначать любыми числами. Поэтому и становится возможным монотонное преобразование одних чисел другими с сохранением прежнего порядка. Пусть, например, объекты с измеряемым признаком получили следующие ранги:

1 2 3 4 5 6.

Эти числа могут быть изменены так, что отношения между рангами останутся неизменными, например:

— 1,5 -1 -0,5 0 0,5 1,0.

Это свойство важно в тех случаях, когда возникает необходимость получения интегрированной оценки, выраженной в одной шкале с постоянной величиной заданных интервалов, — появляется возможность суммирования оценок в таких шкалах.

Действительно, когда оцениваемый объект имеет не одно свойство, а ряд свойств, то его общая интегрированная оценка будет представлять собой сумму оценок этих свойств. Так, например, при оценивании преподавателя студентами могут учитываться такие свойства, как: «внешний вид», «знание материала», «умение доходчиво преподнести материал лекции» и т. п. Если все эти свойства оцениваются в шкале порядков в одной и той же шкале с одним и тем же постоянным шагом между рангами и одним и тем же диапазоном, то полученные для каждого преподавателя оценки по отдельным свойствам могут быть просуммированы, а полученная суммарная оценка будет характеризовать преподавателя в целом.

Пример Пусть по итогам сессии студент получил следующие оценки:

• • высшая математика — «неудовлетворительно» (2 балла);
• • история России — «отлично» (5 баллов);
• • психология — «отлично» (5 баллов);
• • линейная алгебра — «отлично» (5 баллов).

Получается, что в среднем студент сдал сессию на 4,25 балла ((5 + + 5 + 5 + 2)/4 = 4,25).

Число 4 в данном случае измерено в метрической шкале (она показывает число оценок), поэтому деление на него вполне возможно и имеет смысл. Однако в порядковой шкале оценок нет числа 4,25! Дать толкование полученному результату невозможно. Что же произошло в результате вышеприведенных действий и как интерпретировать полученный результат? Шкала так и осталась порядковой, но изменился ее диапазон (масштаб). Если раньше в шкале были только числа 2, 3, 4 и 5, то теперь появилось значительно большее количество упорядоченных чисел, а именно:

• • число 2 = (2 + 2 + 2 + 2) / 4;
• • число 2,25 = (2 + 2 + 2 + 3) / 4;
• • число 2,5 = (2 + 2 + 3 + 3) / 4;
• • число 2,75 = (2 + 3 + 3 + 3) / 4 и т. д. до числа 5.

Вместо четырех элементов порядковой шкалы получены 12 упорядоченных элементов. В этой шкале число 4,25 больше, чем число 4 и меньше, чем число 5. Поэтому показатель «средняя оценка за сессию» имеет простую интерпретацию. Как видно, приведенным выше действием мы просто расширили диапазон шкалы.

Пусть по итогам сессии один студент сдал ее со средним баллом 4,75, а другой — со средним баллом 3,25. Поскольку и для первого, и для второго студента используется одна и та же шкала с одним и тем же количеством элементов в ней, сравнение полученных результатов имеет смысл. Мы можем сказать, что первый студент учится лучше, чем второй. Но можно ли получить ответ на вопрос: во сколько раз лучше сдал сессию первый студент, чем второй? Казалось бы, надо просто разделить 4,75 на 3,25. В результате получим: 4,75/3,25 = 1,461 538.

Что означает полученный результат? Ничего! Числа 1,461 538 в той шкале, с которой мы работаем, просто не существует! Шкала начинается с числа 2. Любые попытки интерпретации полученного результата будут неверными. Поэтому на поставленный вопрос получить ответ невозможно — порядковая шкала ограничивает наши познавательные возможности.

Часто для объективной оценки уровня знаний преподаватели используют систему тестов — формализованную систему оценки ответов на закрытые вопросы. При этом при ответе на вопрос необходимо подчеркнуть один из предлагаемых вопросов или же ответить «да» или «нет». Допустим, что имеется 10 вопросов. В случае правильного ответа выставляется единица, в случае неправильного — ноль. Число правильных ответов подсчитывается, и на их основе выставляется соответствующая оценка:

• • «отлично», если получено 9 или 10 баллов;
• • «хорошо», если получено 7 или 8 баллов;
• • «удовлетворительно», если получено от 4 до 6 баллов;
• • «неудовлетворительно», если получено до 3 баалов.

В данном случае также используются порядковые шкалы. Сначала используется шката оценки ответа на вопрос, которая предусматривает два числа, — 1 или 0. Число 0,24 здесь, очевидно, не существует.

Затем полученные оценки суммируются и получается та же порядковая шкала, но ее диапазон (масштаб) увеличился — от 0 до 10. Увеличилось и количество возможных чисел. Их, как легко подсчитать, стало уже 11.

После этого шкала вновь преобразуется в другую порядковую шкалу — шкалу принятых в вузе оценок: «отлично», «хорошо», «удовлетворительно», «неудовлетворительно» или 5, 4, 3 и 2.

Одна из характеристик, используемых для оценки порядковой шкалы — это «медиана». По сути, она делит ранжированный упорядоченный ряд значений пополам, т. е. 50% оценок находятся до этого значения, а 50% — после него.

Пример Пусть 10 экспертов оценили вкус мороженого на 1 балл; 15 — на 2 балла; 20 — на 3 балла и 5 экспертов — на 4. Выполним расчет медианы для этого случая (табл. 2.16).

Всего к экспертизе было привлечено 50 экспертов (10 + 20 + 15 + 5). Тогда относительная частота ответов по той или иной оценке будет находиться отношением числа экспертов, давших эту оценку, к общему числу экспертов (например, относительная частота экспертов, давших оценку в один балл, будет равна 10 / 50×100% = 20%). Эти цифры занесены в третью строку таблицы.

Расчет медианы по условному примеру.

Таблица 2.16

Накопленная частота представляет собой сумму всех предыдущих относительных частот. Она характеризует процент экспертов, давших оценку не выше данной. Очевидно, что накопленная частота последней оценки будет равна 100%. Накопленная частота, равная 90%, которая приведена для оценки в 3 балла, говорит о том, что 90% экспертов оценили свойства объекта на 3 балла и ниже. Медиана в данном случае будет равна 2 баллам, так как именно для этой оценки характерна граница в 50% ответов. В случае если медиана не выпадает на границу (как с примером в табл. 2.16), медианой будет считаться то значение, в котором происходит переход за 50%. Мода, как легко увидеть, приходится на оценку, равную трем, так как относительная частота этого ответа является наибольшей. Мода и медиана могут совпадать либо отличаться друг от друга, как в этом примере.

Так как оценки каждого из показателей, измеренных в ранговой шкале, упорядочены, то можно анализировать, насколько эти порядки показателей одного и того же объекта исследования совпадают или отличаются друг от друга, т. е. можно говорить о том, являются ли эти факторы взаимосвязанными. Взаимосвязь, очевидно, проявляется так: если с ростом ранга одного признака его количества меняются аналогично количеству другого признака при росте его ранга, данные признаки являются взаимосвязанными. Эту взаимосвязь вычисляют с помощью различных методов ранговой корреляции, чаще всего используя коэффициенты ранговой корреляции Спирмена и Кендалла.

Если проранжированные показатели свойств x_t и y_t t-то объекта имеют один и тот же диапазон рангов от 1 до Г, то коэффициент ранговой корреляции Спирмена будет вычисляться по формуле^[5]

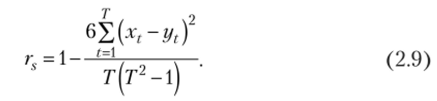
Если этот коэффициент по модулю близок к единице, то говорят о сильной линейной взаимосвязи между этими показателями, если он близок по модулю к нулю, то это свидетельствует об отсутствии линейной взаимосвязи.

Для работы с так называемыми «связанными рангами» (одинаково важными рангами) этот коэффициент оказался непригодным. Так, например, если некоторое свойство товаров Г и Д эксперт оценивает как равное, он придает им одинаковую оценку, и в шкале порядков товары будут занимать следующие друг за другом ранги, имеющие одинаковые оценки. Эта ситуация и получила название «связанных рангов». В этом случае рекомендуется использовать коэффициент ранговой корреляции Кендалла, который будет иметь вид¹:

Здесь Р — число совпадений для пар рангов. Под «совпадением» понимается одинаковый порядок оценок пар рангов. Например, первым экспертом товару, А присвоен ранг 1, а товару Б — ранг 3. Необходимо посмотреть, сколько еще экспертов дают товару, А более высокий ранг, чем товару Б. Это и есть число совпадений.

Пример Покажем, как информацию, измеренную в шкале порядков, можно использовать для выявления взаимосвязи между показателями с помощью коэффициента ранговой корреляции Спирмена (2.9). В табл. 2.17 приведен пример результатов ранжирования 10 товаров по нескольки м показателям.

Таблица 2.17

Ранги десяти товаров.

Там же. С. 164.

Таблица 2.18

Посмотрим, насколько, по мнению экспертов, взаимосвязаны два показателя — качество товара и его престижность. Расчеты коэффициента приведены в табл. 2.18.

Расчет коэффициента ранговой корреляции Спирмена.

Теперь можно рассчитать соответствующий коэффициент ранговой корреляции:

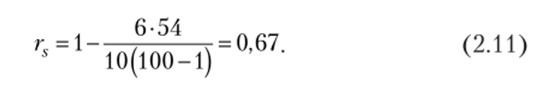
Если этот коэффициент по модулю близок к единице, то говорят о сильной линейной взаимосвязи между показателями, если он близок по модулю к нулю, то это свидетельствует об отсутствии линейной взаимосвязи. В нашем случае коэффициент приближается к величине 0,7, что ближе к единице. Поэтому можно говорить о том, что взаимосвязь между рассматриваемыми факторами существует, хотя и не очень тесная.

Операции с числами, измеренными в интервальных шкалах, помимо всех перечисленных выше действий, включают в себя следующие новые^[7]:

• 1) числа могут быть линейно преобразованы в другие числа;
• 2) для определения степени взаимосвязи используется более чувствительный коэффициент парной корреляции Пирсона.

Если с числами порядковой шкалы можно было осуществлять только монотонные преобразования, то линейные преобразования более сложны и имеют вид:

Это означает, что, получив значение х в шкале интервалов, исследователь может его преобразовать в новое число у с помощью соотношения (2.12). Как видно, к числам теперь можно не только прибавлять некоторую константу, но и умножать их на число соотношения между интервалами, их расстояния при этом не изменятся. Числа в интервальной шкале можно складывать или вычитать, находить средние арифметические или средние взвешенные. В шкале порядков число, равное 5,345, не имеет никакого смысла, так как между числами 5 и 6 в этой шкале нет и не может быть никакого расстояния, поэтому остаток от целого числа не дает никакой информации. Более того, такой остаток совершенно бессмыслен. В шкале интервалов это число показывает, насколько оно близко к соседним целым числам — 5 и 6.

С учетом того, что в шкале интервалов нулевое значение не означает полного отсутствия свойства, то отношения чисел друг к другу не имеет особого смысла, хотя эти операции и могут выполняться. Покажем это на простом примере.

Одна из самых известных интервальных шкал — шкала температур по Цельсию. Если сегодня температура воздуха в городе составила +ГС, а завтра — +5° С, то это не означает, что температура воздуха выросла в пять раз. В этом легко убедиться, если перейти к новой шкале измерения температуры — по Фаренгейту. Ранги температур в обеих шкалах остаются неизменными, а вот отношения между ними получаются разными. Если такую же операцию провести с числами метрической шкалы, то мы увидим принципиальное отличие — отношения чисел в метрической шкале имеют смысл. Для того чтобы убедиться в этом, разделите среднемесячную заработную плату по России в настоящее время на ежемесячную стипендию студента российского вуза в то же время. А теперь переведите измеренные доходы в доллары, немецкие марки или японские йены и вновь найдите отношения среднемесячной зарплаты по России к сти;

пендии российского студента. Вы убедитесь в том, что это отношение осталось неизменным.

Этот пример показывает, что не все математические операции с числами в шкале интервалов можно осуществлять так, как нам этого хотелось бы. Линейные преобразования имеют смысл, нелинейные — бессмысленны.

В то же время, наличие расстояния между числами значительно обогащает возможности вычисления степени взаимосвязи между показателями, измеренными в шкале интервалов. Конечно, в этом случае можно воспользоваться и всеми предыдущими способами вычисления степени взаимосвязи, но более точно это можно сделать с помощью коэффициента корреляции Пирсона, который будет нами изучен в параграфе 3.6.

Числа, полученные с помощью метрической шкалы, могут быть обработаны с помощью всего арсенала методов математической статистики, включая методы, применимые для шкал более низкого уровня.

• [1] Рузавин Г. И. Логика и аргументация: учеб, пособие. М.: Культураи спорт; ЮНИТИ, 1997. С. 64.
• [2] Типология и классификация в социологических исследованиях. М. :Наука, 1982. С. 96.
• [3] Ядов В. А. Стратегия социологического исследования. Описание, объяснение, понимание социальной реальности. М.: Добросвет; Книжныйдом «Университет», 1998. С. 160—161.
• [4] Ядов В. Л. Стратегия социологического исследования. Описание, объяснение, понимание социальной реальности. С. 169—170.
• [5] Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс, 1976. С. 160.
• [6] яснение, понимание социальной реальности. С. 172—173.
• [7] Ядов В. Л. Стратегия социологического исследования. Описание, объ