Р-адические числа Кольцо m-адических чисел

Рассмотрим десятичную дробь 273,35. Если после цифры 5 поставить многоточие, то получим бесконечную десятичную дробь: 273,35… Поставленные три точки означают, что после пятерки следует бесконечный «хвост» цифр. Примем смелое решение и перед первой цифрой рассматриваемого числа поставим многоточие с аналогичным смыслом, то есть считаем, что в записи …273,35 цифре 2 предшествует вполне определенная «дорожка» цифр. Полученную таким образом запись будем называть 10-одическим числом. Обобщим эту ситуацию и введем общее понятие.

5.8.1. Определение. Зафиксируем натуральное число т> 1 и назовем т-адическим числом всякую запись вида .л_/,₊₂я"+100…0,.

л+1.

где буквы с индексами обозначают цифры ш-ичной системы счисления, а многоточие в начале записи указывает на наличие вполне определенной бесконечной последовательности цифр. Если цифры после запятой отсутствуют, то запись называется целым т-адическим числом.

Например, 10-адическими числами будут …0023; …273; …36,273; …00,00. При т-1 получаем 7-адические числа, например, …352,03₇, …26,06_?, 10₇. Если основание системы счисления указано отдельно, то в записи числа его можно опускать.

5.8.2. Определение. Два ш-адических числа будем называть равными, если равны их соответствующие цифры.

Множество всех m-адических чисел обозначим через Q_m. Определим на этом множестве сложение, вычитание и умножение по известным правилам «столбиком». Например, для 7-адических чисел имеем:

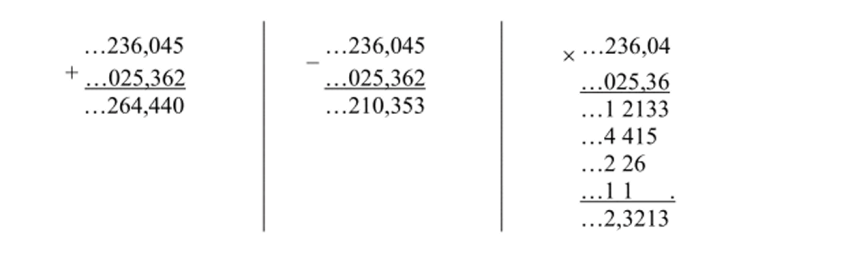
Заметим, что для перехода от привычной десятичной записи «обыкновенного» целого положительного числа к записи его в виде целого 10-адического числа достаточно приписать к нему слева «дорожку» нулей, т. е. записать с нулем в периоде. Например, целое число 24 запишется в виде …0024, или кратко: (0)24. Найдем 10- адическую запись отрицательного целого числа, например, -24. Для этого по правилу вычитания «столбиком» найдем разность:

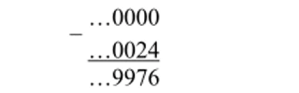
Для проверки сложите «столбиком» числа …9976 и …0024. Таким образом, отрицательные целые числа записываются в виде 10- адических чисел с «дорожкой» девяток, то есть с девяткой в периоде: -(0)24 = (9)76.

При произвольном т положительные целые числа записываются в виде целых /и-адических чисел с нулем в периоде, а отрицательные — с (/и — 1) в периоде. Таким образом, можно считать, что Z cz Q_m.

По аналогии с приближенными значениями десятичных дробей введем аналогичное понятие для /и-адических чисел.

5.8.3. Определение. Для /и-адического числа a = .a_na_n__v.a_x%, a_a_2.a__k /и-адическое число.

а" =…ООа_па_п_₁.д_]а_0ча__]а_₂.л__к назовем приближенным значением числа а. Аналогичный смысл имеют обозначения Д, у_п, 8_п, … для /н-адических чисел Д, у, S…

Понятно, что два w-адических числа равны тогда и только тогда, когда для любого номера п их и-е приближенные значения совпадают.

Из способа сложения «столбиком» вытекает, что у суммы /иадических чисел а + Р и суммы их приближенных значений а_п + Д, все цифры с начальными номерами до цифры с номером п включительно совпадают. То же самое справедливо и для произведений а • Д и а_п • Д,. Используя это, легко доказать, что сложение и умножение m-адических чисел коммутативны, ассоциативны и умножение дистрибутивно относительно сложения.

Докажем, например, свойство ассоциативности сложения. Из сказанного выше вытекает, что сумма (а + Р) + у и сумма приближенных значений (а_п + Р_п) + у_п имеют одинаковые цифры вплоть до н-й. То же самое можно сказать относительно а + (р + у) и а"+(р_п+у"). Но (а_п + Р") + у" = а_п + (Р"+у_п), отсюда и следует совпадение цифр у чисел (а + Д) + / и а+ (Р +у). Следовательно, (а + Д) + у=а + (Д + /).

Очевидно, целые числа 0 и 1, которые теперь записываются в виде /н-адических чисел соответственно …00,00…О и …001,00…0 (с любым количеством нулей после запятой) играют роль соответственно нуля при сложении и единицы при умножении. Для всякого /и-адического числа а существует противоположное /и-адическое число -а. Таким образом, множество 0," относительно сложения и умножения образует кольцо, которое называется кольцом m-адических чисел. Напомним, что оно содержит кольцо целых чисел.

Перейдем к делению /и-адических чисел. Рассмотрим пример деления «уголком» для целых 5-адических чисел. При этом частное будем формировать «справа налево»:

Итак, …1324₅ :.3213₅ = …3013₅. Поясним вычисления. Сначала находим крайнюю правую цифру частного. Нужно найти такую цифру х, чтобы произведение Зх, записанное в пятеричной системе счисления, оканчивалось цифрой 4. Заметим, что НОД (3,5) = 1, поэтому, если в выражении Зх переменная х пробегает значения 0, 1, 2, 3, 4, то остатки от деления 3. x на 5 будут пробегать эти же числа лишь в другом порядке. Остаток от деления Зх на 5 как раз и дает последнюю цифру числа Зх. В нашем случае при х = 3 получаем число 9₁₀ = 14₅. Умножая делитель /? = .3213 на 3, получим 5- адическос число …0144, которое записываем под делимым а = …1324″ и производим вычитание. В остатке получаем …113 (последний ноль не записываем). Теперь аналогично подбираем следующую цифру частного так, чтобы произведение делителя на эту цифру частного оканчивалось цифрой 3. В нашем случае второй цифрой частного следует взять 1. И так далее.

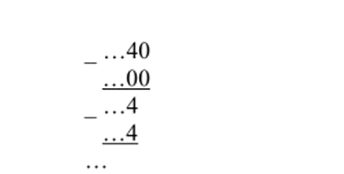
В общем случае, если мы делим /и-адическое число а на т- адическое число р 0 и последняя цифра делителя, обозначим ее через Ь, взаимно проста с т, то числа 6−0, bТ, Ь-2, …, b (m-1) при делении на т дают различные остатки, а значит множество остатков совпадает с множеством цифр 0, 1, 2, …, т-1. Таким образом, в этом случае возможность подбора очередной цифры частного гарантирована и деление возможно. В частности, когда т — р — простое число, деление возможно всегда. Действительно, в этом случае делитель р * 0 можно представить в виде р = Р' •(10_/>)^я, где р' — целое /7-адическое число, не оканчивающееся нулем, то есть последняя цифра числа р' взаимно проста с р. Деление на р' возможно, а деление на Р добавляет еще перемещение запятой на соответствующее число знаков (влево, если л 0). Таким образом, кольцо О_р при простом р является полем.

Пусть при делении «уголком» произвольного целого /н-адического числа а на целое m-адическое число Р ф 0 «под уголком» получили w-адическое число у-.с_пс_п__х.с^. Докажем, что / действительно является частным отделения а на /?, то есть р-у = а. Рассмотрим шаги алгоритма деления «уголком».

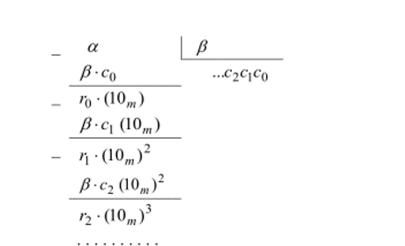
Сначала подбираем цифру с₀ и находим разность: а-0с_о = г₀ (10_;/|), отсюда а = 0с_о + г₀(10_/;1 ) = 0/о+ г₀(О_т). Затем подбираем цифру с, и находим разность: г_о(10_ш)-/?с, (1 ()",) = /*, (10,)², откуда.

/О (10″,) = /ic, (10″,) + /,(!о,)² и, а = рс₀ + /Jс, (10,") + г, (10″,)² =.

= 0 (с₀ + с, (10″,)) + /*,(10″,)² = /?•/,+/',(10″,)². На следующем шаге деления получим а = р (с₀ + с, (10″,) + с₂ (10,")²) + r₂ (10″,)³ = = Р? У₂ + г₂ С10,")³, итак далее. Таким образом, для любого л = 0,1,… имеем: а = Р-у_п+ r_n (10_т)" , откуда а — 0 • у" = (10_Ш)". Отсюда следует, что у ш-адических чисел а и 0 у все цифры с начальными номерами вплоть до цифры с номером п совпадают, каково бы ни было п. Следовательно, а = 0-у.

Отметим, что при любом т в кольце Q_m деление возможно на любое натуральное число 0. В самом деле, пусть тр"^х…р^п_к^к — каноническое разложение числа т на простые множители. Число 0 можно представить в виде 0 = 0'• Р™' Р™² —-Р™* > где 0' взаимно просто с т. Найдутся целые неотрицательные числа .г, х₂, …, х_к такие, что ^+:г‘р™^{2 +ЛГг}• • р_к^{к +Х{С} =т^п при некотором натуральном п. В этом случае.

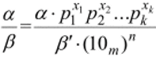
. Таким образом, деление а на 0 сводится к делению числа a-pf^lp%²…p_k^k на 0 что обеспечивается взаимной простотой чисел 0' и т, с последующим перенесением запятой на п знаков.

Подметим особенность ш-адической записи рационального числа. Рассмотрим два характерных примера при т = 5:

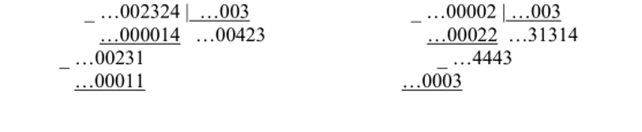
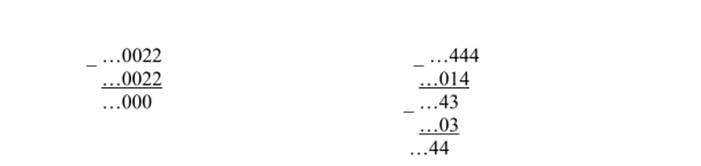
Итак, …2 324₅ :…003₅ = …423₅ = (0)423₅ и …002₅ :…003₅ = …313 1 4₅= (31)4₅. В обоих случаях получаем периодические 5-адические числа. Докажем, что это не случайно. Рассмотрим пристальнее остатки в алгоритме деления «уголком» целого w-адического числа а =…ООа_п.д₁а₀ на целое w-адическое число /?=…00/>,_г./>,/>₀ *0. Каждый остаток имеет в периоде либо 0, либо т-1. Предположим, что каждый остаток имеет 0 в периоде (как в первом примере). Поскольку в каждом следующем остатке количество цифр после нулевого периода все время уменьшается, то на конечном шаге получим нулевой остаток, а значит, в частном будем иметь 0 в периоде. Если же некоторый остаток имеет цифру т — 1 в периоде (во втором примере уже первый остаток …443 имеет 4 в периоде), то и все последующие остатки имеют эту же цифру в периоде. Количество цифр остатка, идущих после периода, ие превосходит количества цифр произведения числа, записанного цифрами делителя /?, идущими после нулевого периода, на очередную цифру частного (во втором примере в каждом остатке после периода из четверок количество цифр не превосходит количества цифр произведения 3 на очередную цифру частного). Поэтому наступит момент, когда мы получим остаток, который ранее уже встречался. Но тогда, начиная с этого момента, цифры частного начнут повторяться, и мы получим в частном периодическое /w-адическое число. Таким образом, всякое рациональное число записывается в виде периодического т-адического числа.

Обратно, всякое периодическое w-адическое число является записью некоторого рационального числа. Покажем на двух характерных примерах как по данной периодической 5-адической записи найти соответствующее рациональное число. Сначала.

выполним проверку представления — в виде 5-адического числа ог = (31)4₅. Умножим это равенство на 100₅ =(10₅)² (поскольку в периоде 2 цифры). Получим ог (10₅)² = (31)4 * (10₅)² =(31)400₅. Тогда ог (10₅)² -а=(31)400₅ -(31)4₅. Выполним вычитание «столбиком»:

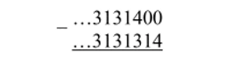
Следовательно, or-(10₅)² -сг = (0)31₅. Но a-(₅)² -a =

a-((10₅)²-1)= «•(…0044₅). Таким образом,.

Еще пример. Пусть [5 = (243)1₅. Найдем соответствующее рациональное число. Умножим это равенство на (10₅)³ (поскольку в л.

периоде 3 цифры). Получим /?• (10₅) = (243)1000₅. Найдем разность:

/? (10₅)³-/(=(243)1000, —(243)1, =(4)3014,. Отсюда.

Наконец, рассмотрим общий случай и найдем рациональное число по его записи в виде периодического m-адического числа. Всякое w-адическое число можно представить в виде суммы целого w-адического числа и дробной части, которая, очевидно, является записью рационального числа. Поэтому можно ограничиться рассмотрением периодического целого ш-адического числа у = (а_п+ка_п+к__{.п,,_+|)а_па_п_₁.//₀. Умножим это равенство на.

(10_т)* (поскольку в периоде к цифр). Получим.

Г ? (¹0,")* = (а_п+ка_п+кА. n_n+l)a_na_n__t. л₀ 0OJ).

к

Найдем разность: у (Ю",)* - У =(а"_+ка«^__]. д»₊, )а"а«_₁.;

к

где d — цифра 0,.

либо цифра (т-1), что соответствует либо положительному, либо отрицательному целому числу. В результате получаем рациональное число у = ^^с«+А^с.?+Л-.1^,?1^сР. Итак, рациональные числа и только 00.)*-1.

они записываются в виде периодических m-адических чисел. Таким образом, О, а О_т.