Ответы, указания и решения

• 1. Предположим противное, что дерево G, содержащее гамильтонову цепь, не является цепью. Пусть А и В — граничные вершины гамильтоновой цепи. Мы знаем, что любые две вершины дерева соединяет единственная цепь (см. определение 2 дерева). Поэтому вершины А и В соединяет только рассматриваемая гамильтонова цепь. Эта цепь включает все вершины дерева (так как она гамильтонова) и проходит через все ребра (так как в противном случае в дереве появится цикл). Следовательно, дерево G является цепью. Полученное противоречие доказывает, что дерево не может содержать гамильтоновой цепи, если оно само не является цепью.
• 2. Двудольный граф, имеющий нечетное число вершин, не может содержать гамильтонова цикла, так как каждый простой цикл в двудольном графе имеет четное число ребер и, следовательно, содержит четное число вершин.
• 3. Если граф содержит гамильтонов цикл, который одновременно является и эйлеровым циклом, то этот граф сам является простым циклом. Если же граф содержит гамильтонову цепь, являющуюся одновременно и эйлеровой цепью, то этот граф сам является простой цепью. Это следует из того, что путь, являющийся одновременно и гамильтоновым и эйлеровым, проходит через все вершины и все ребра.
• 4. Среди 20 вершин графа, изображенного на рис. 65, имеется 5 вершин степени 2. Если бы в графе существовал гамильтонов цикл, то этот цикл обязательно прошел бы через 10 ребер, инцидентных пяти вершинам степени 2. Но, как видно из рисунка, эти 10 ребер сами образуют простой цикл и поэтому не могут быть подмножеством большего простого цикла.
• 5. Предположим сначала, что граф ромбического додекаэдра содержит гамильтонов цикл. Так как этот граф двудольный, то каждое ребро этого цикла связывает вершины из разных «долей». Поэтому количество вершин в «долях» должно быть одинаково. Но данный граф имеет 8 вершин в одной «доле» и 6 вершин в другой. Аналогично, если предположить, что двудольный граф содержит гамильтонову цепь, то придем к выводу, что количества вершин в «долях» могут отличаться не более чем на единицу. Следовательно, граф ромбического додекаэдра не может содержать гамильтонову цепь.
• 6. Если двудольный граф является гамильтоновым (т.е. — содержит гамильтонов цикл или гамильтонову цепь), то количества вершин в его «долях» отличаются не более чем на 1 (см. задачу 5).
• 7. Рассмотрим граф, множество вершин которого состоит из всех 64 позиций на доске 8×8, а множество ребер — это возможные переходы ходом шахматного коня из одной позиции в другую. Тогда задача сводится к отысканию в этом графе гамильтонова цикла. Заметим, что наибольшее значение для степеней вершин этого графа равно 8, и мы не можем применить теорему 9 для доказательства его гамильтоновости. Тем не менее этот граф имеет огромное количество гамильтоновых циклов, дающих решения задачи. Например, два решения приведены на рис. 70.

Замечание. Легко видеть, что если шахматная доска состоит из нечетного числа клеток, то задача об отыскании гамильтонова цикла для шахматного коня оказывается неразрешимой. Действительно, при каждом своем ходе конь попадает на клетку другого цвета, т. е. в соответствующем графе не существует ребер, соединяющих клетки одного цвета. Это означает, что граф — двудольный. Причем, если общее число клеток нечетно, то количество вершин в «долях» различны. Поэтому в этом графе не существует гамильтонова цикла (см. задачи 5 и 6). Можно показать, что если количество клеток четно и каждая сторона прямоугольной доски состоит не менее чем из 5 клеток, то задача имеет положительное решение. Таким образом, размер самой маленькой квадратной доски должен быть 6×6, а размер самой маленькой прямоугольной доски — 5×6.

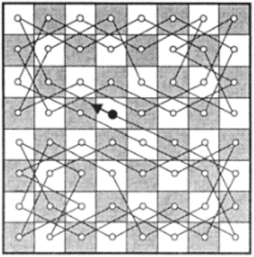
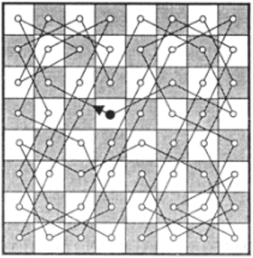
Рис. 70.

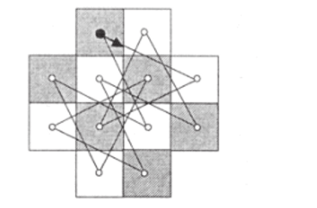
Рис. 72.

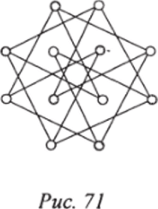
8. Граф, соответствующий условию задачи, представлен на рис. 71. Он является двудольным и связным, содержащим в каждой «доле» по 6 вершин. Один из гамильтоновых циклов, дающих решение задачи, приведен на рис. 72.

9. Реализуем граф кубооктаэдра в виде плоского графа, представленного на рис. 73. Ясно, что в пункте а) ответ положительный, так как в этом графе существует гамильтонов цикл (см., например, рис. 75).

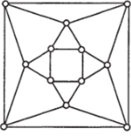
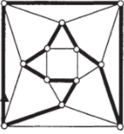
Рис. 73 Рис. 74

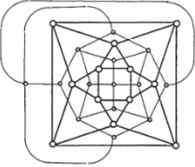
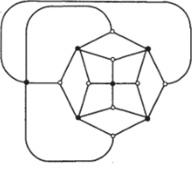
Рис. 75 Рис. 76

В пункте б) ответ отрицательный. Чтобы это доказать, нам снова придется заняться проблемой гамильтоновости графов. Но теперь эту проблему мы будем решать не для графа кубооктаэдра, а для графа, полученного следующим образом. Вершины этого графа являются гранями кубооктаэдра, а ребрами соединяются вершины лишь в том случае, если соответствующие грани кубооктаэдра имеют смежное ребро (см. рис. 75). Этот граф изображен на рис. 76 и является двойственным для графа кубооктаэдра. Легко видеть, что полученный граф изоморфен графу ромбического додекаэдра (см. рис. 67) и не имеет гамильтонова цикла (он двудольный, и количества вершин в «долях» отличаются на 2).

Замечание. Мы попутно доказали, что кубооктаэдр и ромбический додекаэдр двойственны друг другу. Проблемой двойственности мы подробно займемся при изучении плоских графов.