Двухмерные и трехмерные колебания

Простейший пример двухмерных колебаний — результат сложения двух взаимно перпендикулярных одномерных колебаний по оси х и по оси у (рис. 2.80, а). Это может иметь место, если есть две возвращающие силы F_x= - к_хх и F_y = - к_уу. Тогда колебания описываются такими уравнениями.

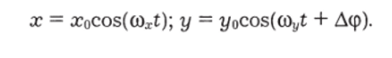
Это означает, что они могут иметь разные частоты, амплитуды и разные фазы, т. е. быть сдвинутыми по фазе на Дер.

Рассмотрим вид суммарного колебания при со* = со_у = со в зависимости от величины А<�р. При Д (р = 0 можно поделить одно уравнение на другое. Получится.

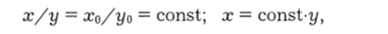
т. е. уравнение прямой линии. В начальный момент времени х = хо и у = з/о (точка А на рисунке 2.80, а). Затем начинают одновременно уменьшаться и ж и у. Точка движется к началу координат, проскакивает его, отклоняется в положение Вит. д., иными словами, колеблется по прямой 1 на рисунке 2.80, а.

При Д<�р = к/2 в начальный момент времени t — 0 х = х, а у = 0, так как cos (ji/2) = 0. Это точка С на рисунке 2.80, а. Затем х начинает убывать, а у = t/ocos (co? + к/2) = - yosin (cot) возрастает по абсолютной величине, но в отрицательной области (точка D). Полный вид траектории можно получить, исключив из формул для х и у время ?. Разделим х на Хо, у на уо, возведем оба уравнения в квадрат и сложим:

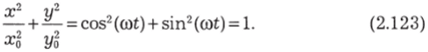
Получается уравнение эллипса с полуосями Хо и у₀. Тело будет двигаться по эллипсу по часовой стрелке, как показано на рисунке 2.80, а, кривая 2.

При 0 < Д (р < л/2 траектория получается промежуточной (кривая 3 на том же рисунке).

При произвольных частотах со* Ф <�л_у траектории получаются сложными. Сравнительно простой вид они имеют, если частоты кратны друг другу, например со_у = 2со_х или <�л_у = Зсо_х и т. д. Тогда колеблющееся тело будет совершать 2 или 3 колебания в одном направлении и за то же время одно колебание — в другом. На рисунках 2.80, б, в, г показаны разные случаи таких колебаний. Получающиеся фигуры называются фигурами Лиссажу.

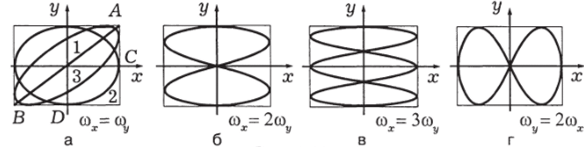
Рис. 2.80.

По виду фигуры можно сразу сказать, какая частота больше и во сколько раз. Нужно только подсчитать число петелек у фигуры.

Для вычерчивания двухмерных колебаний в виде фигур Лиссажу на экране компьютера нужно сделать в программе цикл по времени с шагом At «Т = 2л/о), в котором в каждый следующий момент времени будут вычисляться х и у по формулам (2.121) и (2.122) и ставиться точка с такими координатами.

Пример. Уравнения колебаний вдоль осей х и у запишем в виде.

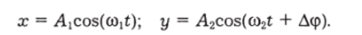
Используем программу Lissaz из пакета ПАКПРО. Введя обозначения Л] = А1; Л₂ = А2; й), = Wl; СО2 = W2 и Дф = F, возьмем какие-либо значения для амплитуд и частот (важны только соотношения между ними) и зададим значение F. По этой программе, изменяя параметры, можно наблюдать, как изменяются траектории точки (фигуры Лиссажу).

Можно рассмотреть и трехмерные колебания. Такие колебания в принципе не отличаются от двухмерных. Добавляется еще одна координата z и возвращающая сила F₂. Тогда все процессы рассматриваются не в плоскости, а в объеме. Нужно в программу, кроме строчек вычисления х и у, добавить строку вычисления 2, например z = z₀cos (cot + ДсрО, а строку, где ставится точка на экран, записать так, как это делается для изображения трехмерных объектов на плоском экране, например ставить точку не с координатами (х, у), а с координатами (х — г/2, у — 2/3). См. программу 3_liss в пакете ПАКПРО. К сожалению, при таком примитивном программировании не будут стираться невидимые линии, но все же интересно поупражняться в создании и толковании таких фигур. Для простоты рекомендуется сначала частоты со_х, со_у и со. взять кратными.