Турбулентное течение. 
Вихри. Лобовое сопротивление

На рисунке 2.65 показано движение тела в жидкости или движение жидкости, обтекающей неподвижное тело. При малых скоростях течение жидкости ламинарное (рис. 2.65, а). При больших скоростях относительного движения течение из ламинарного переходит в турбулентное с образованием позади предмета вихрей, водоворотов (рис. 2.65, б). Причина образования вихрей показана на рисунке 2.65, в. Слой 1 движется быстрее, чем, например, слой 3. Получается, что при наличии вязкого трения на выделенный объем жидкости действует вращающий момент.

Переход от ламинарного течения к турбулентному зависит от комбинации параметров.

где р — плотность, v — скорость, I — размеры тела или препятствия, а Т| — коэффициент вязкости. Величина R получила название числа Рейнольдса. Турбулентность появляется при значениях R порядка 10³.

В случае, а (рис. 2.65) сила трения (сила лобового сопротивления) зависит от вязкости жидкости и согласно (2.100) пропорциональна относительной скорости г>, т. е.

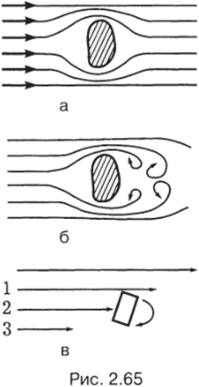
При увеличении скорости за движущимся телом начинают образовываться вихри (рис. 2.65, б). На их образование тратится энергия, и сила трения начинает возрастать быстрее, так что формулы (2.100) и (2.103) уже неверны. Когда судно движется по поверхности воды, энергия тратится также на образование волн на поверхности и эти формулы также несправедливы.

В итоге функция F_Tp (и) становится весьма сложной. Однако это функция гладкая, без особенностей, и она всегда может быть представлена в виде многочлена.

т. е. F_Tp(t;) можно разложить в ряд по степеням v. При v —> 0 сила F_Tp -" 0. Надо учесть, что при изменении знака v на противоположный сила F_Tр должна тоже сменить знак, но остаться по абсолютной величине такой же. Тогда придется положить коэффициенты при четных степенях v равными нулю: А'= В'= … = 0. В результате получается.

При малых v, например г? = 0,1 м/с, значение v³ очень мало (v³ = 10″ ³ м³/с³) и вторым членом Bv³ можно пренебречь. При больших v член Bv³ становится больше Av или даже много больше и им никак нельзя пренебрегать. На рисунке 2.66 приведены зависимости F_Tp от v при разных значениях В (В₃ > В₂ > Вi).

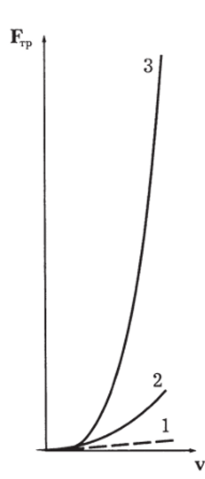
Коэффициенты А, В и т. д. зависят от формы тела, вязкости и ряда других параметров. Их весьма трудно рассчитать теоретически, и они находятся для каждой конкретной ситуации экспериментально. В таблице 2.1 приведены ориентировочные значения, которые можно использовать для оценки F_Tp (г?), но только по порядку величины.

Значения этих коэффициентов можно оценить и самостоятельно, если знать, какую мощность (или какую силу тяги) должен развивать двигатель транспорта или какую силу сопротивления встречает тело при движении с малой скоростью и при движении с большой. Например, тело размером с небольшой камень в воздухе при скорости 1м/с встречает очень небольшое сопротивление (~10 г = 0,1 Н). Следовательно, А = Frp /v ~ 0,1/1 ~ 0,1 Н с/м.

В то же время, набрав при падении скорость около 20 м/с, он падает уже без ускорения, равномерно, т. е. Ft Р равно весу Р = mg. Следовательно, В = Frp/v* ~ 10/8−10³ ~.

— 10″³Н*с³/м³ (при грубой оценке можно пренебречь членом Av, который меньше Bv³ при такой скорости).

При движении ладони в воде I ~ 0,1 м, ка 10³-1 • 10^-1/10″³~ 10⁵. Течение будет Рис. 2.66.

Г| ~ 10″ ³ Нс/м², р =10³ кг/м³ и при v = 1 м/с число Рейнольдса R получается порядка 10³-1 • 10″ ¹/10″³~ 10⁵. Течение будет Порядок значений коэффициентов А и В для оценки F_Tp (и) по формуле (2.104).

Таблица 2.1.

турбулентным. При медленном же движении с v < 1 см/с = 10″ ² м/ с значение R получается меньше 10³, течение можно считать ламинарным и F_Tp = Av.

Для грубых оценок можно руководствоваться приемом: при R « 10³ членом Bv³ в формуле (2.104) можно пренебречь, при R > 10³ — наоборот Bv³ > Av и можно пренебречь членом Av. При R « 10³ нужно учитывать следующие члены разложения.

Лобовое сопротивление F_Tp при том же R можно сильно уменьшить, если по возможности предотвратить образование вихрей за телом. Для этого телу придают обтекаемую форму (рис. 2.67, б). Обратите внимание, что наиболее острый конец делается сзади, а не спереди.

В то же время при очень больших скоростях (сверхзвуковых, когда скорость больше скорости звука) перед самолетом, возникает сильное уплотнение воздуха. Он не успевает расступиться. Поэтому спереди делается острый штырь (рис. 2.67, в), который, как иглой, «протыкает» это уплотнение. При гораздо.

Рис. 2.67.

меньших скоростях подобная ситуация получается при движении судна по воде, так как скорость волн — 5 км/час и скорости судов обычно превышают эту скорость. Получается «сверхволновое» движение, так что переднюю часть быстроходных судов тоже приходится заострять.

Сильную зависимость F_Tp от скорости используют животные при плавании по воде. Если собака двигает лапу назад с большей скоростью, чем вперед, т. е. «бьет лапами по воде», то сила реакции воды при движении лапы назад больше, чем при движении вперед. В результате получается более сильная опора на воду, и собака движется вперед. Так могут плыть по воде животные, совершенно не приспособленные к этой среде (лошадь, кошка). В известной мере этот эффект использует и человек при разных стилях плавания, и рыбы при отталкивании от воды хвостом.