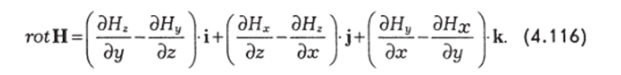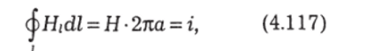Вычисление полей в конкретных ситуациях

Поле в центре кругового тока (рис. 4.41). Определяя направление dH в центре окружности, мы видим, что все векторы dH, создаваемые в этой точке всеми участками <21, направлены одинаково (на рисунке 4.41 — от нас за чертеж). Следовательно, для нахождения общего Н можно просто все элементы I <2Н | складывать арифметически:

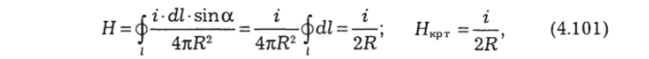
так как для всех элементов, а = 90^е.

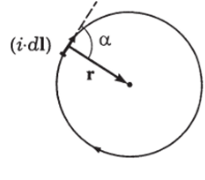
Много сложнее находить поле не в центре кругового тока, а в других точках плоскости витка. Это можно сделать, используя численные методы расчета. Воспользуйтесь программой vitok или mloop в пакете ПАКПРО. Попробуйте установить, где Я больше, в центре или на некотором расстоянии от центра.

Оказывается, из трех чертежей 4.42, а, _рис ^ ^

4.42, б и 4.42, в только 4.42, в правилен.

Еще сложнее вычислить поле не в плоскости витка, а в разных точках пространства вокруг витка. Соответствующая программа Mdipol дана в пакете ПАКПРО.

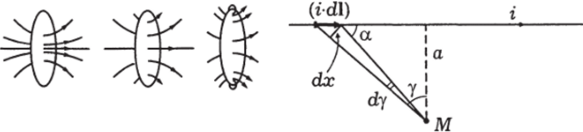
Поле бесконечного прямого провода на расстоянии а от него (рис. 4.43). В этом случае все вектора <2Н, создаваемые всеми участками dl_y тоже направлены одинаково, и их можно просто арифметически суммировать (интегрировать). Но теперь для каждого участка величины, а и г будут разными. Для взятия интеграла удобнее все переменные свести к углу у, провести интегрирование по у от 0 до к/2, т. е. только по половине провода, а затем результат удвоить:

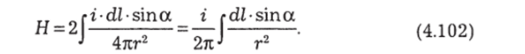
Использовав соотношения из рисунка 4.43.

sina = cosy, dx = dl • sina = dl • cosy, dx = r • dy; a = r • cosy,.

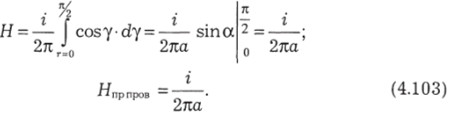
Циркуляция вектора Н по замкнутому контуру Определение циркуляции некоторого вектора по замкнутому контуру уже давалось в разделе 1 данной главы. Для Н это будет.

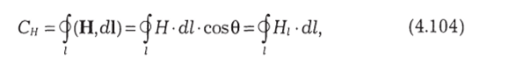
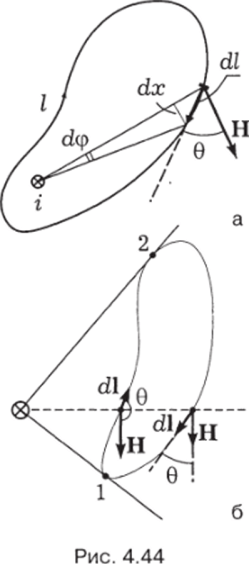
где 0 — угол между Н и dl (рис. 4.44, а).

Рассмотрим два случая — контур охватывает ток (рис. 4.44, а) и не охватывает (рис. 4.44, б).

Будем для простоты считать, что магнитное поле создается прямолинейным проводом с током i, т. е. в любой точке Н = г/(2ка). При повороте на малый угол dip

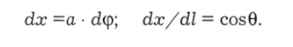
Тогда в первом случае.

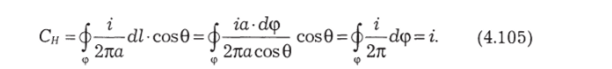
Во втором случае, когда контур не охватывает провод с током, надо брать интеграл по пути от точки 1 до точки 2 по одной стороне контура и от 2 к 1 — по другой:

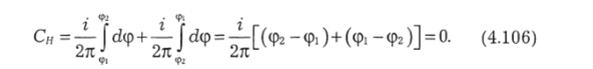
Это означает, что при подсчете циркуляции Сн надо учитывать только те токи, которые пронизывают контур, и не надо те, которые проходят вне его. Циркуляция вектора Н равна алгебраической сумме токов, пронизывающих контур:

Ротор Н Теперь перейдем к дифференциальной форме уравнения (4.107). Будем сжимать контур в точку, т. е. устремим площадь S, охватываемую контуром, к нулю. При этом контур будет охватывать все меньшую и меньшую часть токов (cLCh —> 0) и площадь dS будет также стремиться к нулю. Найдем плотность циркуляции:

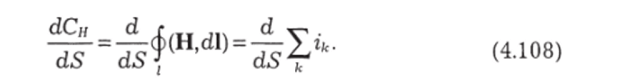
Справа получится плотность тока в данной точке j, a dCn/dS назовем ротором вектора Н в этой точке (rotH). Тогда.

Плотность тока j — это вектор. Таким образом, ротор — это оператор, преобразующий вектор Н в вектор j.

В отличии от электростатического поля, где rotE = 0, в магнитном поле rot Н Ф 0. Это связано с иной природой магнитного поля. Силовые линии магнитного поля нигде не начинаются и нигде не кончаются, они замыкаются сами на себя. Такое поле называется вихревым. Отличие циркуляции по замкнутому контуру или ротора от нуля — это признак вихревого поля.

Отвлечемся на время от природы магнитного поля и рассмотрим внимательнее оператор rot. На рисунке 4.45 показаны линии тока жидкости (поле вектора скорости v). В некоторых местах могут быть источники (в точке А, например, подводится вода из крана, в точке В расположено сливное отверстие, и часть воды может в него уходить). В этих точках div * 0. Но кроме того, в токе жидкости могут образовываться водовороты или вихри, например за камнем К. В этих местах вода крутится и, если поместить в точку С вертушку с лопастями (мельничное колесико), то она будет вращаться. В точке С rotv * * 0, а в точке D, где вихрей нет, rotv = 0. Направление вектора rotv определяется правилом буравчика. В точке С ротор направлен на нас, в точке Е — от нас за чертеж. См. также рис. 4.46.

Чтобы понять, почему отличие ротора от нуля является признаком вихря, рассмотрим этот оператор в координатной форме, т. е. найдем его составляющие в прямоугольной системе координат х_у у, z (рис. 4.47). Возьмем сначала контур I в виде прямоугольника abed, лежащего в плоскости х, у. Если мы найдем циркуляцию для такого контура dC_H = L H_tdl и разделим на dS, мы определим составляющую ротора вдоль оси z.

Пусть в точке а составляющие вектора Н равны Н_х, Н_у и Н_г. Начнем обход контура с движения вдоль ab. Если контур мал, можно приближенно считать, что на протяжении каждой стороны прямоугольника Я/ постоянна и равна Я, в начальной точке. Так что при движении вдоль dx составляющая Я/ = Я_г и.

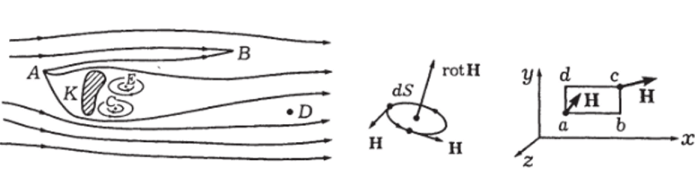
Рис. 4.45.

Рис. 4.46

Рис. 4.47.

При перемещении вдоль Ьс

Здесь мы учли, что Н_у могло измениться при смещении на dx и к Н_у добавили скорость изменения, умноженную на смещение dx.

На участке cd

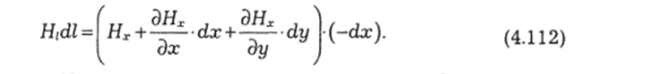
Здесь учтено, что Я_х может изменяться и от смещения на dx и от смещения на dy. На участке da

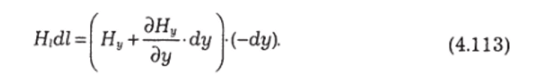
Для получения циркуляции по всему контуру сложим эти четыре выражения и, учитывая, что некоторые слагаемые взаимно уничтожаются, получаем:

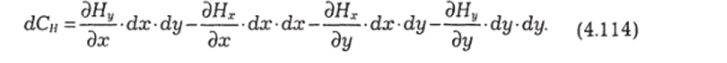
Если разделить это на площадь контура dx dy, то получится составляющая ротора вдоль оси z:

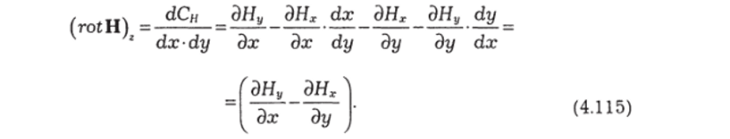
Из рисунка 4.48 можно понять смысл такой разности. Если линии Н образуют вихрь, например против часовой стрелки, то Н_у с увеличением х.

(ЭНу А (Эн* А _.

возрастает —->0, а Н_х с увеличением у уменьшается -<0 .Если.

(Эх J (ду

есть вихрь, то разность (4.115) отлична от нуля и положительна.

Аналогичным образом можно получить составляющие ротора по другим осям:

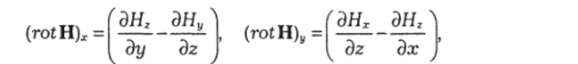
а весь оператор rot в координатной форме будет