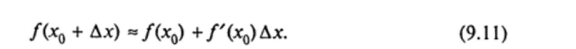Определение и геометрический смысл дифференциала
Поскольку для функции у = /(х), дифференцируемой в точке эс0, приращение Ду в этой точке может быть представлено в виде формулы (9.6), слагаемое А Ах при Ах —" 0 является бесконечно малой одного порядка с Аху тогда как второе слагаемое в формуле (9.6) бесконечно малая более высокого порядка; иными словами, величина А Ах — главная часть приращения Ду, обусловленного приращением аргумента Дх.
Определение 5. Дифференциалом функции у — /(х0) в точке х0 называется главная линейная относительно Ах часть приращения функции в этой точке:
Поскольку из теоремы 9.1 следует, что А = /'(х0), эту формулу можно переписать в виде 
Дифференциалом dx независимой переменной х будем называть приращение этой переменной Дх, т. е. соотношение (9.7) принимает вид.
Из равенства (9.8) производную /'(х) в любой точке х можно вычислить как отношение дифференциала функции dy к дифференциалу независимой переменной dx: 
Равенство (9.6) с учетом теоремы 9.1 и формулы (9.8) можно переписать в виде.
что полностью соответствует определению дифференциала функции.
Дифференциал функции имеет четкий геометрический смысл (рис. 9.3). Пусть точка М на графике функции у —/(х) соответствует значению аргумента х0, точка N — значению аргумента х0 + Дх, MS — касательная к кривой /(х) в точке М, ф — угол между касательной и осью Ох. Тогда МЛ — приращение аргумента, AN — соответствующее приращение функции. Как видно из треугольника ABMt АВ = Дх tg ф = /'(х0) Дх = dy, т. е. это главная по порядку величины Дх и линейная относительно ее часть приращения функции Ду. Второе слагаемое в уравнении (9.10) более высокого порядка малости соответствует отрезку BN.
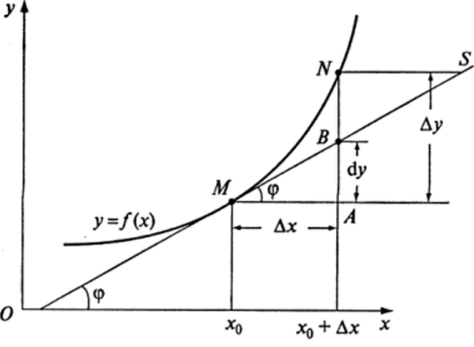
Рис. 9.3.
Приближенные вычисления с помощью дифференциала
Приближенные вычисления с применением дифференциала функции основаны на приближенной замене приращения функции в точке на ее дифференциал:
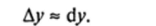
aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">
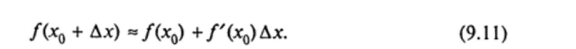
Формула (9.11) является основной в приближенных вычислениях. Соответствующий пример будет приведен ниже.
Абсолютная погрешность от такой замены является, как следует из формулы (9.10), при х > 0 бесконечно малой более высокого порядка по сравнению с Дх. Подставляя в это приближенное соотношение формулу (9.8) и выражение для Ду, получаем:

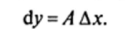





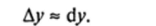 aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">
aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">