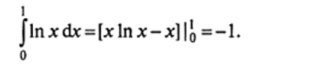Интегралы от неограниченных функций

Рассмотрим функцию/(х), определенную на промежутке [а, b), но нс ограниченную на нем. Для определенности положим. что/(х) ограничена и интегрируема на любом отрезке а> b — е), 0 < е < b — а, но нс ограничена в любой окрестности точки b или на промежутке [Ь — 8, Ь]. В таком случае точка Ь называется особой точкой.

Ь-с

Определение 4. Предел интеграла J /(*)dx при е —> 0 называется несоб-

а

ственным интегралом второго рода и обозначается.

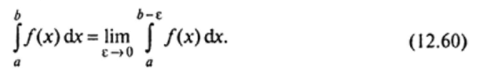
Если этот предел конечным, то говорят, что интеграл (12.60) существует или сходится, а функцию / (х) называют интегрируемой на промежутке а, Ь) если же предела нет или он бесконечен, то говорят, что интеграл (12.60) расходится.

Аналогично, если особой является точка л: = я, то несобственный интеграл второго рода определяется как.

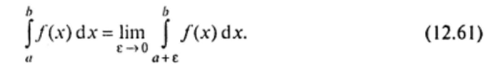
Если функция /(л) не ограничена в окрестности некоторой внутренней точки с е (я, Ь, то по определению полагают:

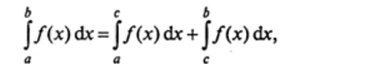
где несобственные интегралы второго рода в правой части этого равенства определяются соответственно по формулам (12.60) и (12.61).

Наконец, если а и b — особые точки, т. е. функция /(х) ограничена и интегрируема на интервале (я, b)_t то несобственный интеграл второго рода определяется в виде суммы: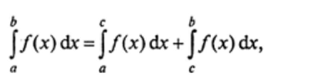

где с — произвольная точка на (я, />), а несобственные интегралы второго рода в правой части этого равенства определяются по формулам (12.61) и (12.60) соответственно.

Рассмотрим несколько примеров на вычисление несобственных интегралов второго рода с применением предельного перехода.

Пример 21. Вычислить интеграл особая точка х = 1.

ov^1-*.

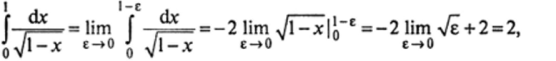
Решение. По формуле (12.60) получаем: т. е. данный интеграл сходится.

dx.

Пример 22. Вычислить J, две особые точки: -I и 1.

Решение. Разобьем этот интеграл на два, используя внутреннюю точку х = О интервала (-1, 1):

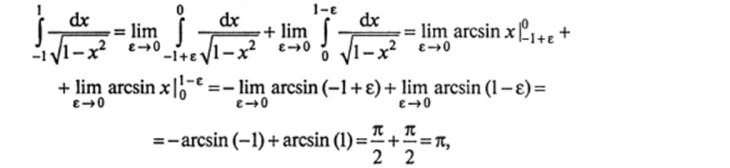
следовательно, данный несобственный интеграл второго рода сходится.

Пример 23. где, а > 0 — некоторое число; х = 0 — особая точка.

Решение. Рассмотрим два случая разных значений числа а: 1) а = I. Тогда имеем:

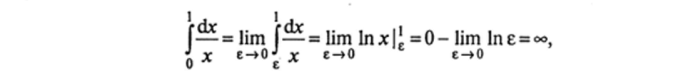
т.е. при, а = 1 несобственный интеграл расходится; 2) при, а * 1 получаем:

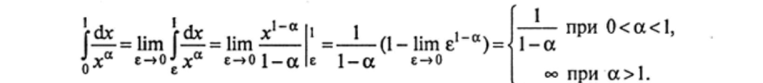
Следовательно, данный интеграл расходится при, а > 1 и сходится при 0 < а < 1.

По аналогии с несобственным интегралом первого рода можно обосновать применение основной формулы интегрального исчисления для несобственного интеграла второго рода. Пусть функция /(х) интегрируема на промежутке [j, b)_t причем b является для нес особой точкой. Если для /(х) существует первообразная F (x), имеющая предел в особой точке х = b или непрерывная на отрезке [а, Ь]у то для вычисления несобственного интеграла второго рода имеет место обычная формула Ньютона — Лейбница:

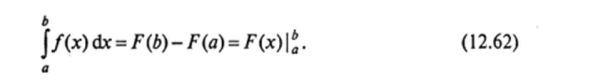
Та же формула справедлива и в том случае, когда особая точка находится внутри промежутка интегрирования, однако при этом непременным является условие непрерывности первообразной функции в особых точках.

Рассмотрим примеры применения формулы Ньютона — Лейбница.

Пример 24. Вычислить интеграл Jx~^2/3dx.

Решение. Здесь особая точка х = 0, однако, так как первообразная функция Зх^,/3 непрерывна в этой точке, данный интеграл существует:

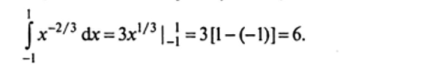
Пример 25. Найти интеграл f.

_₂^Х —

Решение. Этот интеграл нс существует, поскольку первообразная In |д:² — 11 обращается в бесконечность в особых точках х = ±1.

Пример 26. Вычислить интеграл Jin хdx.

о.

Решение. Здесь особая точка х — 0. Первообразная функция, определяемая с помощью интегрирования по частям, имеет вид х In х — х. При х -" 0 се предел равен нулю, и потому данный интеграл сходится: