Двумерная случайная величина

Определение 2.7. Двумерная случайная величина — это пара случайных чисел (X, Y), или точка на координатной плоскости (рис. 2.11).

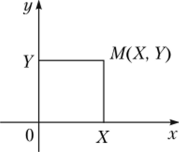
Рис. 2.11. Двумерная случайная величина.

Двумерная случайная величина — это частный случай многомерной случайной величины, или случайного вектора.

Определение 2.8. Случайный вектор — это случайная функция ?,(/) с конечным множеством возможных значений аргумента t, значение которой при любом значении t является случайной величиной.

Двумерная случайная величина называется непрерывной, если ее координаты непрерывны, и дискретной, если ее координаты дискретны.

Задать закон распределения двумерных случайных величин — это значит установить соответствие между ее возможными значениями и вероятностью этих значений. По способам задания случайные величины делятся на непрерывные и дискретные, хотя есть общие способы задания закона распределения любой СВ.

Дискретная двумерная случайная величина Дискретная двумерная случайная величина задается с помощью таблицы распределений (табл. 2.1).

Таблица 2.1

Таблица распределения (совместное распределение) СВ (X, У).

Элементы таблицы определяются формулой.

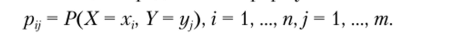
Свойства элементов таблицы распределения:

1) Р*>0;

п т

2) I? л, = 1.

Распределение по каждой координате называется одномерным или маргинальным:

р^1> = Р (Х = .г,) — маргинальное распределение СВ X;

р^²⁾ = P (Y= у,) — маргинальное распределение СВ У.

Связь совместного распределения СВ X и У, заданного множеством вероятностей [р_{)}, i = 1,…, n, j = 1,…, т (таблицей распределения), и маргинального распределения.

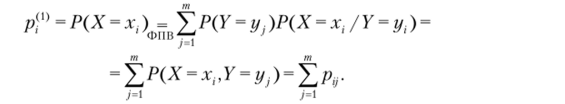
И.

Аналогично для СВ Ур-²⁾ = X р,_г

1 = 1.

Задача 2.14. Дано:

Найти маргинальные распределения.

Решение

Из связи совместного и маргинальных распределений получим следующие маргинальные ряды распределений СВ X и У:

Непрерывная двумерная случайная величина.

/(х, y)dxdy — элемент вероятности для двумерной случайной величины (X, У) — вероятность попадания случайной величины (X, У) в прямоугольник со сторонами cbc, dy при dx, dy —* 0:

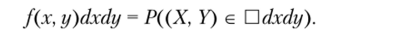
f (x, у) — плотность распределения двумерной случайной величины (X, У). Заданием /(х, у) мы даем полную информацию о распределении двумерной случайной величины.

Маргинальные распределения задаются следующим образом: по X — плотностью распределения СВ X/,(х); по Y — плотностью распределения СВ Уf>(y).

Задание закона распределения двумерной случайной величины функцией распределения Универсальным способом задания закона распределения для дискретной или непрерывной двумерной случайной величины является функция распределения F (x, у).

Определение 2.9. Функция распределения F (x, у) — вероятность совместного появления событий {Х<�х} и {У<у}, т. е. F (x₀, y_n) = = Р (Х < х₀, У < г/₀)^— это вероятность точки с координатами (х, у), брошенной на координатную плоскость, попасть в бесконечный квадрант с вершиной в точке М (х₀, у_и) (в заштрихованную на рис. 2.12 область).

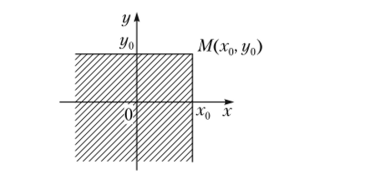
Рис. 2.12. Иллюстрация функции распределения F (х, у).

Свойства функции F (x, у)

• 1) 0 < 1;
• 2) F (-oo, -оо) = F (x, -оо) = F (-oo, у) = 0; F (оо, оо) = 1;
• 3) F (x, у) — неубывающая по каждому аргументу;
• 4) F (x, у) — непрерывна слева и снизу;
• 5) согласованность распределений:

F (x, оо) — маргинальное распределение по X: F (x, оо) = F,(x); F (y, оо) — маргинальное распределение по Y F (оо, у) = F₂(y). Связь /(х, у) с F (x, у):

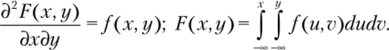
Связь совместной плотности с маргинальной. Дана f (x, у). Получим маргинальные плотности распределения f (x), f₂{y)'.

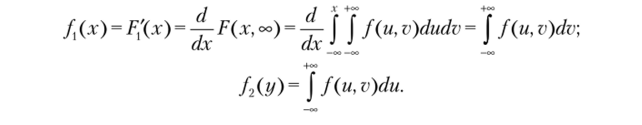
Случай независимых координат двумерной случайной величины Определение 2.10. СВ Xи Yнезависимы (нз), если независимы любые события, связанные с каждой из этих СВ. Из определения нз СВ следует:

• 1 )Pij = p^X)pf
• 2 )F (x, y) = F_l(x)F₂(y).

Оказывается, что для независимых СВ X и Y выполнено и.

3 )f (x, y) = J (x)f,(y).

Докажем, что для независимых СВ X и Y 2) 3). Доказательство, а) Пусть выполнено 2), т. е.

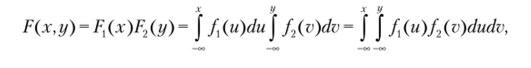
л- У

в то же время F (x, y) = f J f (u, v) dudv, откуда и следует 3);

б) пусть теперь выполнено 3), тогда.

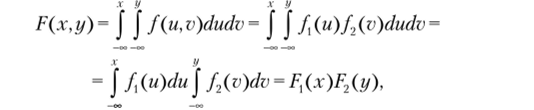
т.е. верно 2).

Рассмотрим задачи.

Задача 2.15. Распределение задано следующей таблицей:

Зависимы ли СВ X и У? Построить /'(.г, у). Решение

Строим маргинальные распределения:

Получаем Р (Х = 3, У = 4) = 0,17 * Р (Х = 3) Р (У = 4) = 0,1485 => => СВ X и Узависимы.

Функция распределения:

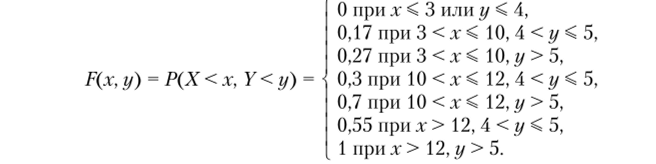
Задача 2.16. Распределение задано следующей таблицей:

Зависимы ли СВ X и У?

Решение

Строим маргинальные распределения:

Получаем P_tl = 0,2 • 0,3 = 0,06; Р₁₂= 0,2? 0,7 = 0,14; P_2l = 0,8? 0,3 = = 0,24; Р₂₂ — 0,8 • 0,7 = 0,56 => СВ X и Y нз.

Задача 2.17. Дана /(х, у) = 1/я • ехр| -0,5(д' + 2ху + 5г/²)]. Найти А (х) и /Ау) —

Решение

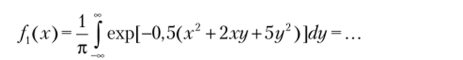
(досчитайте самостоятельно).