Синтез систем с переменной структурой

Для того чтобы изображающая точка, находящаяся в состоянии х (s (x) Ф 0), двигалась в сторону поверхности скольжения, необходимо и достаточно, чтобы при s (x) > 0 производная по времени s (x) в силу уравнений (8.4) была отрицательна, а при s (x) < 0 — положительна. Таким образом, условие попадания изображающей точки на поверхность скольжения имеет вид. Рассмотрим, с какой фазовой скоростью… Читать ещё >
Синтез систем с переменной структурой (реферат, курсовая, диплом, контрольная)
Системы с переменной структурой (СПС) второго порядка были рассмотрены в гл. 2, где было продемонстрировано, как методом фазовой плоскости синтезировать СПС. Там, в частности, было показано, что в некоторых случаях можно получить скользящий режим — движение по вырожденной траектории. За счет организации скользящего режима можно обеспечить системе управления нужные свойства в условиях неполной информации — в условиях, когда не известна точная модель объекта управления или его свойства непредвиденным образом изменяются в широких пределах в процессе функционирования системы. В данной главе рассматриваются задачи синтеза СПС произвольного порядка, функционирующего в скользящем режиме.
В общем случае для того чтобы СПС, в которой создается скользящий режим, была устойчива, необходимо и достаточно, чтобы выполнялись следующие три условия: 1) условия попадания; 2) условия скольжения; 3) условия устойчивости скользящего движения. Рассмотрим эти условия.
Условия скольжения и попадания.
Пусть система с переменной структурой описывается уравнениями.
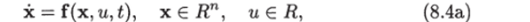
Здесь f (x, u, t) — непрерывная функция, удовлетворяющая условию Липшица; и+(х, ?), u"(x, t) — непрерывные функции и u+(x, t) ф Ф tx_(x, ?); s (x) — непрерывная функция, определяющая поверхность переключения.

Поверхность S, определяемая уравнением s (x) = 0, делит пространство состояний Ап на два подпространства: подпространство А* = {х: s (x) 0}. Правая часть уравнения (8.4а) f (x, u, t) в силу уравнения (8.46) на поверхности S терпит разрыв. Однако существуют левые и правые пределы: 
Производная по времени функции s (x) в силу уравнения (8.4а) имеет вид 
Градиент grad s (x), как известно, направлен по нормали к поверхности 5 в сторону возрастания функции переключения s (x), т. е. в сторону, где s (x) > 0 (рис. 8.2, а). Поэтому если предел 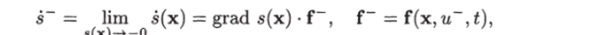
больше нуля (s >0), т. е. угол между векторами grad s (x) и f острый, то вектор f" направлен в сторону подпространства А" .
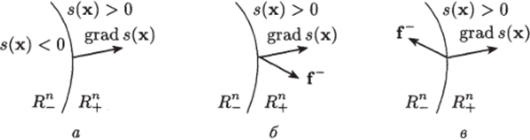
Рис. 8.2. Поверхность переключения.
(рис. 8.2,6). Если указанный предел меньше нуля (s~ < 0), то вектор f" направлен в сторону подпространства А" (рис. 8.2, в). Аналогично, если предел.
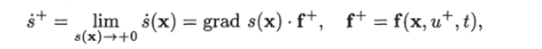
больше нуля ($+ >0), то вектор f+ направлен в сторону подпространства А+, если меньше нуля (s+ < 0), то вектор f+ направлен в сторону подпространства А".
Точки на поверхности переключения 5 можно разделить на три типа [7].
К первому типу относят точки, в которых произведение s~ • s+ положительно: • s+ > 0. В этих точках векторы f~ и f+ направлены в одну сторону (рис. 8.3, отрезок ВС).
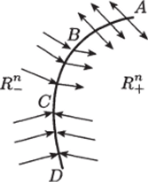
Рис. 8.3. Три типа точек на поверхности переключения.
Ко второму типу относят те точки, в которых Г < 0 и s+ > 0. В этих точках вектор f" направлен в сторону подпространства Л", а вектор /+ — в сторону подпространства Я", т. е. они направлены в разные стороны от поверхности переключения (рис. 8.3, отрезок АВ).
Третий тип составляют точки, в которых выполняются условия.
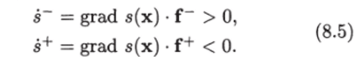
В этом случае векторы f" и f+ направлены к поверхности переключения, т. е. фазовые траектории у поверхности 5 направлены встречно. В случае попадания изображающей точки в эту группу точек на поверхности S начинается процесс скольжения (рис. 8.3, отрезок CD). Условие (8.5) называется условием существования скольжения или просто условием скольжения; поверхность переключения, состоящая из точек третьего типа, называется поверхностью скольжения.
Указанные три типа точек в общем случае отделяются друг от друга многообразием, на котором или s~ — 0, или s+ = 0, или выполняются оба эти равенства.

Рис. 8.4. Определение фазовой скорости на участке скольжения.
На поверхности переключения правая часть уравнения (8.4а) терпит разрыв. Однако в точках первого и второго типов этой поверхности описание движения изображающей точки вопросов не вызывает, так как в непосредственной близости от этой поверхности она движется с фазовой скоростью f" или f+, а на самой поверхности значение ее скорости не играет роли, так как изображающая точка при попадании на одну из точек первого или второго типа мгновенно сходит с поверхности. Проблема возникает при описании скользящего режима, т. е. при попадании изображающей точки на одну из точек третьего типа на поверхности S. Это связано с тем, что при скользящем движении фазовая скорость изображающей точки не равна ни f «, ни f+.
Рассмотрим, с какой фазовой скоростью происходит движение изображающей точки в процессе скольжения, т. е. чему должна быть равна правая часть уравнения (8.4а) при описании движения в скользящем режиме. Пусть точка L лежит на поверхности 5, через которую проходит траектория скольжения (рис. 8.4). Проведем векторы f" и f+, выходящие из этой точки.
Соединим концы этих векторов прямой и найдем точку М пересечения этой прямой с касательной плоскостью к поверхности 5 в точке L. Считается, что в точке L скорость скольжения совпадает с вектором LM [7, 2].
Для того чтобы изображающая точка, находящаяся в состоянии х (s (x) Ф 0), двигалась в сторону поверхности скольжения, необходимо и достаточно, чтобы при s (x) > 0 производная по времени s (x) в силу уравнений (8.4) была отрицательна, а при s (x) < 0 — положительна. Таким образом, условие попадания изображающей точки на поверхность скольжения имеет вид.

Это условие называют условием попадания.