Формирующий фильтр. 
Теория автоматического управления. 
Многомерные, нелинейные, оптимальные и адаптивные системы

Формирующим фильтром называется звено, формирующее из белого шума случайный процесс с заданной спектральной плотностью.

Пусть на вход устойчивого линейного стационарного звена (фильтра) подается белый шум V (t) с единичной интенсивностью (рис. 11.1): р_ис

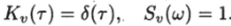
В установившемся режиме выходной сигнал X (t) будет стационарным. Как известно из 1-го тома, его спектральная плотность связана с спектральной плотностью входного сигнала соотношением.

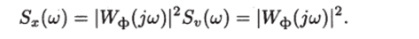
Отсюда следует: чтобы сформировать стационарный случайный процесс с заданной спектральной плотностью 5_х(щ), которую можно представить в виде.

где все полюсы функции tp (s) расположены в левой полуплоскости, достаточно принять передаточную функцию фильтра №ф ($), равной ip{s):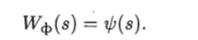

Как мы увидим далее, важно, чтобы не только полюсы, но и нули функции tp (s) располагались в левой полуплоскости.

Представление функции S_x(co) в виде (11.6) называется ее факторизацией.

Факторизация спектральной плотности. В простейших случаях факторизация спектральной плотности и нахождение передаточной функции формирующего фильтра не представляет труда. Например, случайный процесс с корреляционной функцией К_х(т) = = 0е~^атI имеет спектральную плотность.

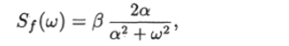
которая может быть представлена в виде.

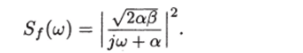
Поэтому передаточная функция формирующего фильтра такого процесса будет иметь вид.

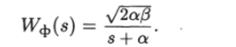
В более сложных случаях можно воспользоваться общим методом факторизации.

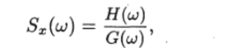
Пусть спектральная плотность S_x(co) является дробно-рациональной функцией:

где #(и;), G (w) — полиномы от cj, а дисперсия конечна:

Спектральная плотность 5_x(w) обладает следующими свойствами:

• 1) S_x(co) — четная функция, причем полиномы Н (a;), G (co) содержат только четные степени со;
• 2) в силу условия (11.7) (S_x(co) -> 0 при со оо) степень полинома Н (со) строго меньше степени полинома G (co);
• 3) в силу (11.7) уравнение G (co) = 0 не имеет действительных корней;
• 4) корни уравнений Н (со) = 0 и G (co) = 0 расположены симметрично относительно обеих осей системы координат.

Пусть полиномы H (lj) и G (lj) имеют вид.

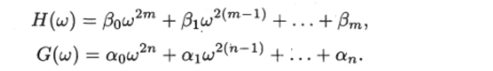
Разложим их на элементарные множители и представим спектральную плотность в виде.

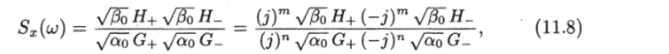
где #₊, G+ — произведения элементарных множителей, соответствующих корням уравнений Н (и) = 0 и G (u;) = 0, расположенным в верхней полуплоскости; - произведения элементарных множителей, соответствующих корням уравнений Н (си) = 0 и G (u>) = О, расположенным в нижней полуплоскости.

Положим.

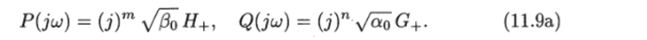
Тогда имеют место следующие равенства:

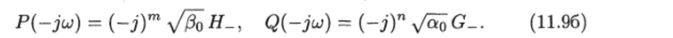
Действительно, пусть а + j (5 (а ^ 0, & > 0) — один из корней уравнения H (lj) = 0. Тогда его корнями будут такжеа — jf3> а — j0 и —а 4— jfi. Этим корням будут соответствовать следующие множители в полиномах Н+ и.

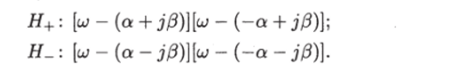
Этим множителям в выражениях (j)^mH+ и соответствуют следующие множители:

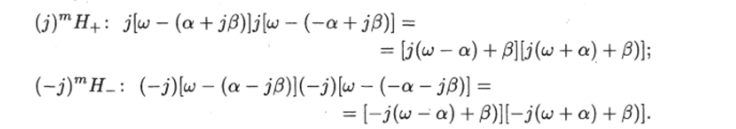
Правые части приведенных двух соотношений являются комплексносопряженными выражениями.

Итак, используя обозначения (11.9), соотношение (11.8) можно представить в виде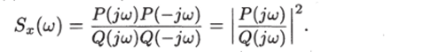

Отсюда для передаточной функции формирующего звена получаем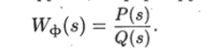

Заметим, что корням уравнений Н{ш) = 0 и G (oj) = 0, расположенным в верхней полуплоскости на плоскости корней и, на плоскости 5 = juj соответствуют левые корни. Поэтому в соответствии с построением полиномов P (s) и Q (s) все нули и полюсы передаточной функции формирующего фильтра располагаются в левой полуплоскости.

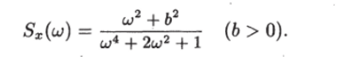
Пример 11.1. Определить передаточную функцию формирующего фильтра для стационарного случайного процесса со спектральной плотностью Решение. В данном случае нулями спектральной плотности ЯВЛЯЮТСЯ UJ = jbj U)2 = ~jb ПОЛЮСаМИ ЯВЛЯЮТСЯ UJ = j, LJ2 = -j,.

CJ₃ = j, lj4 = —j. Поэтому имеем.

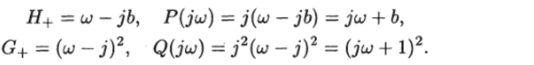
Передаточная функция формирующего фильтра есть W (s) =.

= (_S + 6)/(s+l)².